1 семестр МП / Лабы / LAB10

Лабораторная работа № 10

Изучение упругих свойств пружины

Цель работы: изучение упругих свойств пружины, изготовленной из проволоки круглого сечения; определение двумя методами коэффициента жесткости пружины и расчет модуля сдвига материала проволоки.

Оборудование: установка, пружина, платформа с грузами, ручной секундомер, штангенциркуль, микрометр.

Продолжительность работы - 4 часа.

Теоретическая часть. Описание установки

Рассмотрим спиральную пружину, один конец которой закреплен, а к другому подвешен груз массой Под действием силы тяжести груза пружина растягивается на некоторую величину При этом возникает сила упругости пружины , которая согласно закону Гука пропорциональна удлинению пружины:

(1)

Коэффициент пропорциональности называется коэффициентом жесткости пружины.

Если груз находится в равновесии, то сила тяжести груза уравновешивается силой упругости пружины (пружину считаем невесомой). Из условия равновесия груза следует, что

(2)

Выражение (2) можно использовать для определения коэффициента жесткости пружины. Такой метод определения называется статическим.

Если груз вывести из состояния равновесия и затем отпустить, то он начнет совершать колебания в вертикальном направлении. При малых отклонениях груза от положения равновесия колебания будут гармоническими. Период таких колебаний определяется выражением

(3)

Измерив период колебаний груза известной массы, с помощью формулы (3) можно определить коэффициент жесткости пружины. Этот метод определения называется динамическим.

Зная коэффициент жесткости пружины, ее радиус , число витков пружины и радиус проволоки можно рассчитать модуль сдвига материала проволоки из которой изготовлена пружина:

(4)

Вывод формулы (4) приведен в приложении.

Экспериментальная часть

Упражнение 1. Определение коэффициента жесткости пружины статическим методом.

Подвесьте к пружине пустую платформу. По линейке определите координату нижнего края платформы. Помещая на платформу грузы разной массы определите с помощью линейки удлинения пружиныи постройте график зависимости от (согласно выражению (2) эта зависимость должна быть линейной). По угловому коэффициенту прямой рассчитайте коэффициент жесткости пружины.

Упражнение 2. Определение коэффициента жесткости пружины динамическим методом.

Подвесьте к пружине пустую платформу известной массы; измерьте с помощью секундомера время, за которое она совершают 50 колебаний; рассчитайте период этих колебаний. Нагружая платформу грузами, повторите измерения.

Постройте график зависимости от массы грузиков (зависимость, как следует из формулы (3), должна быть линейной). Определите угловой коэффициент и рассчитайте коэффициент жесткости пружины.

Применив выражение (4), определите модуль сдвига материала проволоки, из которой изготовлена пружина.

Литература

1. Сивухин Д.В. Общий курс физики. - М.: Наука, 1979. - Т. 1. -§§ 39, 40, 78, 79.

2. Савельев И.В. Курс физики. - М.: Наука, 1989. - Т. 1. - § 13.

3. Савельев И.В. Курс общей физики. - М.: Астрель, 2001. - Т. 1. -§§ 2.9, 8.1, 8.4.

4. Иродов И.Е. Механика. Основные законы. - М.: Физматлит,

2001. - § 6.1.

Приложение

Вывод зависимости коэффициента жесткости пружины от ее параметров

Рассмотрим спиральную пружину, изготовленную из проволоки круглого сечения, растянутую силой действующей вдоль ее оси (рис.П1). Шаг пружины будем считать малым по сравнению с ее радиусом.

Мысленно разрежем проволоку пружины в произвольной точке А.

П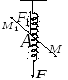усть - сила, с которой верхняя часть пружины действует на нижнюю в месте разреза. Для равновесия нижней части пружины необходимо, чтобы силы и были равны по величине (пружину считаем невесомой). Силы и образуют пару сил, а момент пары сил не зависит от точки, относительно которой он вычисляется. Относительно точки модуль момента этих сил равен

(П1)

Рис.П1. Возникновение кру- Из-за малости шага витков пружины можно тящего момента проволоки считать, что момент в точке направ-

при растяжении пружины лен вдоль оси проволоки. Для сохранения

рассматриваемой части пружины в равновесии необходимо, чтобы возникало кручение проволоки вокруг ее оси, компенсирующее момент Так как растягивающая сила действует вдоль оси пружины, величина момента не меняется вдоль проволоки. Поэтому кручение проволоки является равномерным.

Установим связь между растяжением пружины и полным углом закручивания проволоки.

Мысленно разрежем пружину вертикальной плоскостью, проходящей через ее ось (рис.П2,а). Теперь каждый из участков пружи-

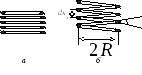
Рис.П2. Разрез пружины: а - в нерастянутом состоянии;

б - в растянутом состоянии

ны, прилегающих к местам разреза (на рисунке - темные точки), закрутим на малый угол (остальные участки пока будем считать недеформированными). Так как на каждый виток пружины приходится по два таких участка (рис.П2,б), то суммарный угол закручивания проволоки будет определяться следующим образом:

, (П2)

где- число витков пружины.

При таком закручивании длина пружины увеличивается на величину

, ( П3)

где - изменение шага пружины, равное (см. рис.П2,б)

(П4)

Из выражений (П2) - (П4) получим зависимость между удлинением пружины и углом закручивания проволоки:

.

Повторив эти рассуждения для других участков пружины и просуммировав удлинения, найдем, что растяжение пружины и полный угол закручивания проволоки связаны следующим соотношением:

. (П5)

Определим, как угол закручивания связан с растягивающей силой Для этого выделим из проволоки цилиндрическую трубку радиусом длиной и толщиной Вырежем из трубки малый элемент, площадь верхней грани которого, определяемая углом , равна (рис.П3,а).

Рис.П3. Положение элемента проволоки до закручивания (а)

и после закручивания (б)

Повернем верхнее основание трубки относительно нижнего на малый угол . При этом боковые грани элемента, лежащие в сечении трубки, повернутся на малый угол (рис.П3,б).

Углы и малы, поэтому нетрудно найти связь между ними:

(П6)

В результате закручивания трубки элемент будет испытывать деформацию сдвига.

Закон Гука для деформации сдвига (где - касательное напряжение) можно записать в виде

, (П7)

где - касательная сила, возникающая при сдвиге и стремящаяся вернуть элемент в исходное положение; - площадь верхней грани элемента; - модуль сдвига.

Подставив соотношение (П6) в выражение (П7) и приняв во внимание, что , для силы получим:

.

Момент этой силы относительно оси трубки равен

.

Просуммировав моменты касательных сил по верхнему основанию рассматриваемой трубки (т.е. проинтегрировав по углу ) и по радиусу проволоки (т.е. проинтегрировав по ), найдем результирующий момент всех касательных сил, действующих в сечении проволоки:

.

При равновесии пружины этот момент равен моменту силы, растягивающей пружину, определяемому выражением (П1)

. (П8)

Производная представляет собой угол закручивания, приходящийся на единицу длины проволоки. Согласно выражению (П8) величина постоянна и, следовательно, равна

, (П9)

где - длина проволоки; - полный угол закручивания проволоки (см. формулу (П5)).

С учетом соотношения (П9) выражение (П8) можно переписать в виде

,

где - коэффициент жесткости пружины.

Из последнего уравнения следует выражение (4) для модуля сдвига проволоки, используемое в работе.

74