2 семестр МПиТК / 2-й семестр / Лекции Соколова / 2_10

Условный экстремум

Вспомним ранее доказанную лемму из линейной алгебры:

Лемма (линейной алгебры):

Пусть в пространстве заданы линейно независимые вектора , где m < n. Если m = n, то эти вектора являются базисом в и любой вектор по ним раскладывается. В нашем случае это необязательно. Условие о том, что некоторый вектор раскладывается по векторам равносильно следующему условию: .

Доказательство этого утверждения мы приводить не будем, т.к. на коллоквиуме его доказывать не нужно.

Введем определение локального условного экстремума.

Пусть задана функция и функции , где i меняется в промежутке , где m<n.

Рассмотрим множество , такое что .

Точка называется точкой условного максимума функции f на множестве E, если существует окрестность , такая что выполняется неравенство . Т.е. экстремум не на всей окрестности, а на некоторой ее части, где .

Рассмотрим функцию - это седло. У нее экстремумов нет. Если мы будем ее рассматривать на окружности , у этого седла найдется экстремум. Фактически мы ищем экстремум на поверхности, но не на всей, а рассеченной какой-то другой поверхностью. Строим над этой окружности цилиндр и получаем уже линию. На этой линии мы и должны найти экстремум.

Необходимое условие локального экстремума.

Пусть функцияимеет частные производные, а функции имеет непрерывные частные производные .

Обозначим множество .

Рассмотрим некоторую точку . Предположим, что – условный экстремум при условиях , это означает в окрестности .

Предположим, что в некоторой окрестности

Эта матрица представляет из себя следующее:.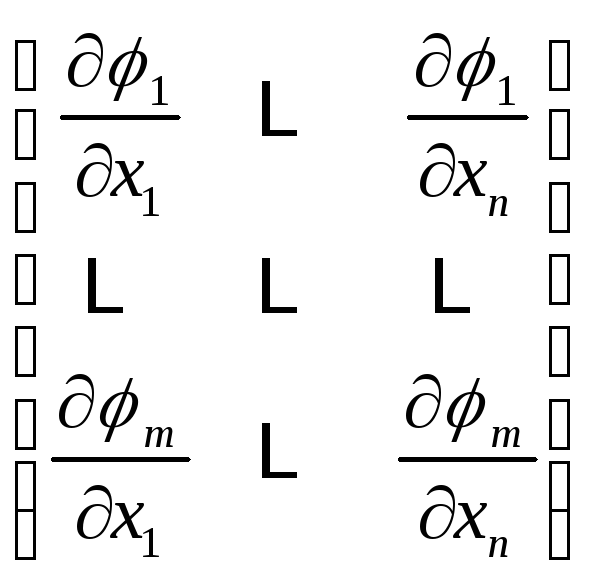

Это означает, что найдется определитель порядка , неравный нулю: в этой окрестности, причем .

Будем рассматривать как неявную функцию переменных:

………….

Тогда на Е . (*)

Но так как точка – точка условного экстремума для функции, следовательно - локальный абсолютный экстремум для .

.

Но нам ведь не интересно выражать это условие через какую-то функцию , которой у нас нет. Если условия связи у нас линейные, то хорошо находятся, но так бывает далеко не всегда. Поэтому нам важно условие выразить в терминах только тех функций, которые у нас есть в условии. Вот этим мы сейчас и будем заниматься.

Запишем дифференциал от левой и правой частей (*), форма первого дифференциала инвариантна:

.

В точке :

, следовательно . Это равенство можно записать и по-другому. В сумме множители представляют из себя координаты вектора градиента. У нас получается, что на любом векторе 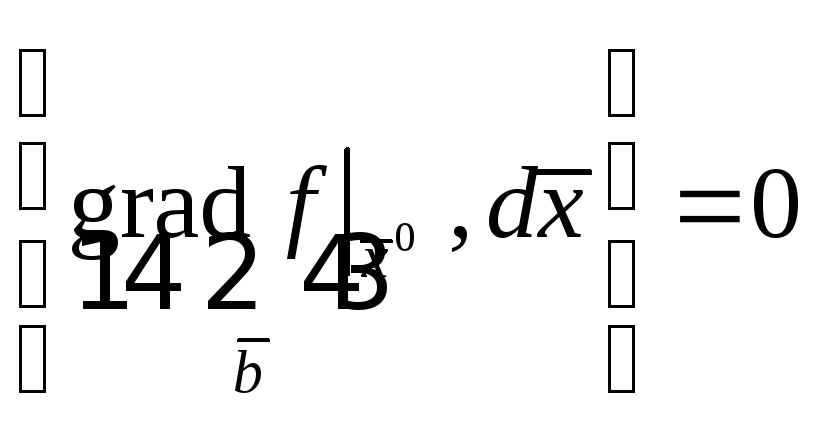на Е. (1) Но это не для любых , а для тех, которые у нас удовлетворяют уравнениям связи. Нас не волнует, что происходит с другими приращениями.

Запишем дифференциальные уравнения связи.

У нас уравнения связи выглядят следующим образом: , где . Мы получаем, что дифференциальные уравнения выглядят таким образом:

на Е. Это равенство тоже можно записать по-другому:

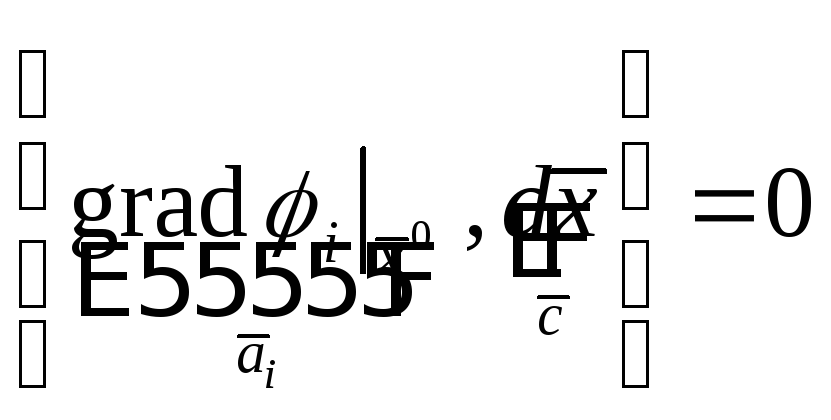(2).

Тогда мы практически получаем нашу лемму о линейной алгебре.

Уравнения 1 и 2 только для тех , для которых выполняется дифференциальное уравнение связи.

. По лемме получаем:

.

Можем записать это условие покоординатно:

………..

- функция Лагранжа.

Тогда эти условия запишутся в виде для , удовлетворяющих уравнениям связи.

У нас получается система:

- необходимое условие существования условного экстремума.

Достаточное условие существования условного экстремума.

. Нам надо выяснить, когда точка является точкой условного экстремума.

Составим при выполнении условий связи. И хорошо бы все это выразить через и .

На множестве Е:

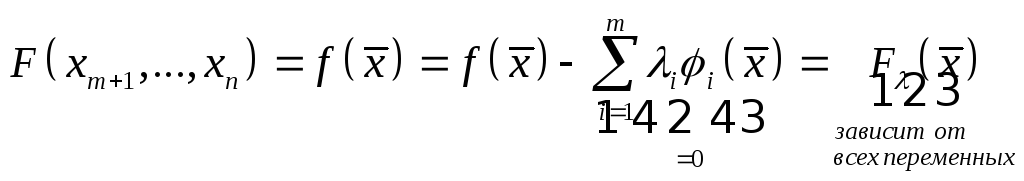
Мы считали второй дифференциал, чтобы посмотреть его значение в точке .

- по необходимому условию.

Если , удовлетворяющего дифференциальным уравнениям связи, , тогда

1) - минимум

2) -максимум

3) или и - ничего сказать нельзя.

4) или - экстремума нет.

Пример. Вернемся к примеру в начале лекции: при условии .

То есть .

Составим функцию Лагранжа

.

; ; ;

Получаем 4 точки , , , ..

при

в :

- максимум.

- аналогично.

Задачи на наибольшее и наименьшее значение.

Пусть задана - замкнутая ограниченная.

Функция- непрерывна на и имеет непрерывные частные производные на внутренности либо на границе.

1) - задача об абсолютном локальном экстремуме.

2) - ищем условный экстремум.

3) Сравниваем.

Пример