
- •Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
- •Ограниченность интегрируемой функции.
- •Суммы Дарбу. Их Свойства.
- •Суммы Дарбу и интегрируемость функции по Риману.
- •Основная теорема о существовании определенного интеграла Римана.
- •Равномерная непрерывность функции. Модуль непрерывности.
- •Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ().
- •Интегрируемость по Риману непрерывной функции.
- •Интегрируемость по Риману монотонной функции.
- •Аддитивное и однородные свойства определенного интеграла Римана.
- •Неравенства для определенного интеграла Римана и теорема о среднем.
- •Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
Пусть
задана функция f(x)
на отрезке
![]() .
Составим разбиениеR:
.
Составим разбиениеR:
![]() .
.
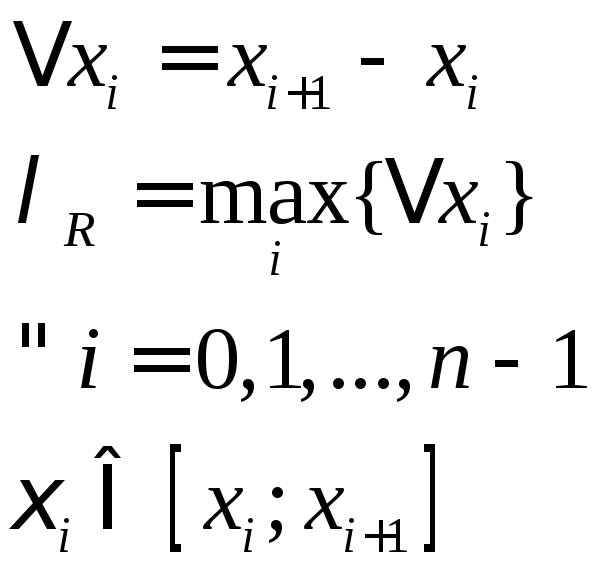
![]()
Это
интегральная сумма, соответствующая
разбиению R
и выбору точек
![]() .
.
Если
существует предел при
![]() интегральных
сумм
интегральных
сумм![]() ,
и он не зависит отR
и
,
и он не зависит отR
и
![]() ,
то он называется определенным
интегралом Римана.
,
то он называется определенным
интегралом Римана.
Определение по Коши:
![]()
![]()
По Гейне:
![]() ,
где
,
где
![]() -
последовательность разбиений.
-
последовательность разбиений.
Критерий Коши:
![]()
![]()
Ограниченность интегрируемой функции.
Теорема:
Если
функция f(x)
интегрируема на [a,b]
и существует
![]() ,
то функция ограничена на этом отрезке.
,
то функция ограничена на этом отрезке.
Доказательство:
От
противного: пусть f(x)
неограничена на [a,b].
Введем произвольное разбиение R:
![]() .
Т.к. функция неограниченна на [a,b],
то она неограничена хотя бы на одном из
отрезков
.
Т.к. функция неограниченна на [a,b],
то она неограничена хотя бы на одном из
отрезков
![]() .
Пусть
.
Пусть
![]() -
номер того отрезка, на котором функция
неограниченна. Тогда рассмотрим
интегральную сумму:
-
номер того отрезка, на котором функция
неограниченна. Тогда рассмотрим
интегральную сумму:
![]() -
т.е. выделили суммы одно слагаемое.
Обозначим
-
т.е. выделили суммы одно слагаемое.
Обозначим
![]() ,
тогда получим:
,
тогда получим:
![]() (следует
из неравенства о модулях). Тогда возьмем
произвольное N
и сделаем разность
(следует
из неравенства о модулях). Тогда возьмем
произвольное N
и сделаем разность
![]() .
Для этого у нас должно быть
.
Для этого у нас должно быть![]() .
У нас функция неограниченна на отрезке
.
У нас функция неограниченна на отрезке![]() ,
значит
,
значит![]() .
Тогда интегральная сумма будет
.
Тогда интегральная сумма будет![]() ,
т.е. будет являться величиной неограниченной,
т.е. не будет существовать ее предела,
а значит и
,
т.е. будет являться величиной неограниченной,
т.е. не будет существовать ее предела,
а значит и![]() ,
что противоречит условию.
,
что противоречит условию.
Теорема доказана.
Суммы Дарбу. Их Свойства.
Определение:
Пусть
![]() ограничена
на отрезке
ограничена
на отрезке![]() .
Введём разбиениеR
этого отрезка.
.
Введём разбиениеR
этого отрезка.
R:
![]() ,
,
![]() .
.
Тогда можем составить выражения:
![]() - нижняя сумма
Дарбу,
- нижняя сумма
Дарбу,
![]() - верхняя сумма Дарбу.
- верхняя сумма Дарбу.
![]() ,
,
![]() .
.
Свойства сумм Дарбу:
1)
![]() ,
для одного и того же разбиения.
,
для одного и того же разбиения.
2) Рассмотрим два
разбиения в случае, когда одно разбиение
является продолжением другого. Т.е.
![]() -
продолжение
-
продолжение![]() ,
если все точки
,
если все точки![]() являются точками
являются точками![]() .
.
![]() ,
,
т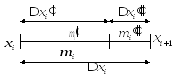 .е.
добавление точек не увеличивает
.е.
добавление точек не увеличивает![]() и не уменьшает
и не уменьшает![]() .
.
Доказательство:
Пусть
![]() получается из
получается из![]() добавлением одной точки.
добавлением одной точки.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
Заметим, что если
![]() ,
то
,
то![]() и
и![]() .
Отсюда заключаем:
.
Отсюда заключаем:
![]() ,
,
![]() ,
,![]() ,
,![]() .
Аналогично для
.
Аналогично для![]()
3) Для любых двух
разбиений одного и того же отрезка
нижняя сумма Дарбу не превосходит
верхней:![]()
![]() .Доказательство:
.Доказательство:
Пусть
![]() - объединение двух разбиений, тогда
- объединение двух разбиений, тогда![]() ,
,![]() ,
тогда по свойству 2
,
тогда по свойству 2
![]() ,
т.е.
,
т.е.
![]()
![]() .
.
4)
![]()
![]() - нижний интеграл (нижняя точная сумма
Дарбу).
- нижний интеграл (нижняя точная сумма
Дарбу).![]()
![]() .
.
![]()
![]() - верхний интеграл
(верхняя точная сумма Дарбу).
- верхний интеграл
(верхняя точная сумма Дарбу).
![]()
![]() .
.
![]() .
.
Суммы Дарбу и интегрируемость функции по Риману.
Теорема:
Функция
![]() интегрируема на отрезке
интегрируема на отрезке![]() тогда и только тогда, когда
тогда и только тогда, когда![]() .
.
Доказательство:
Докажем необходимость условия:
Функция
![]() интегрируема на отрезке
интегрируема на отрезке![]() .
.
Пусть
![]() ,
тогда
,
тогда![]()
![]()
![]() ,
т.е.
,
т.е.![]() .
.
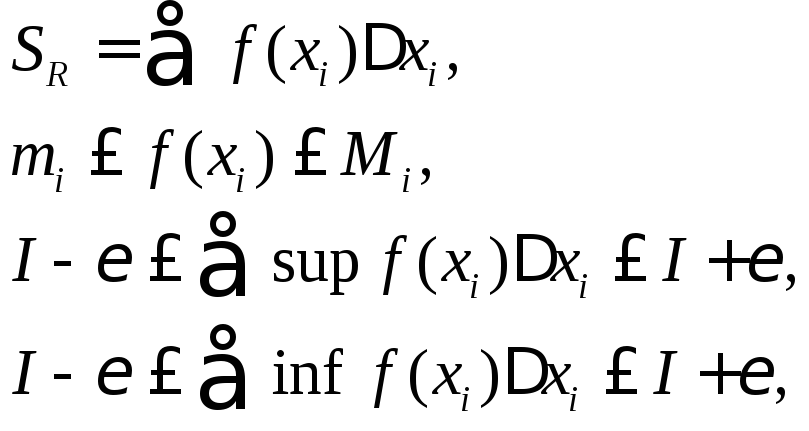
т.е.
![]() и
и![]() .
.
Далее
имеем:
![]() ,
т.е.
,
т.е.![]() .
.
Необходимость доказана.
Докажем достаточность условия:
![]() .
.
![]()
![]()
![]() .
.
![]() .
.
Докажем,
что
![]() .
.
Нужно:
![]()
![]() ,
т.е.
,
т.е.![]()
Имеем:
![]()
![]() тогда по определению
тогда по определению
![]()
![]()
![]() ,
,
![]() ,
тогда по определению
,
тогда по определению
![]()
![]()
![]() ,
,
т.е.
![]()
![]() .
.
Достаточность доказана.
Основная теорема о существовании определенного интеграла Римана.
Теорема (Основная)
Ограниченная
функция f
интегрируема на отрезке [a,b]
тогда и только тогда, когда
![]() .
.
Доказательство:
П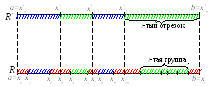 о
теореме об интегрируемости (f интегрируема
о
теореме об интегрируемости (f интегрируема
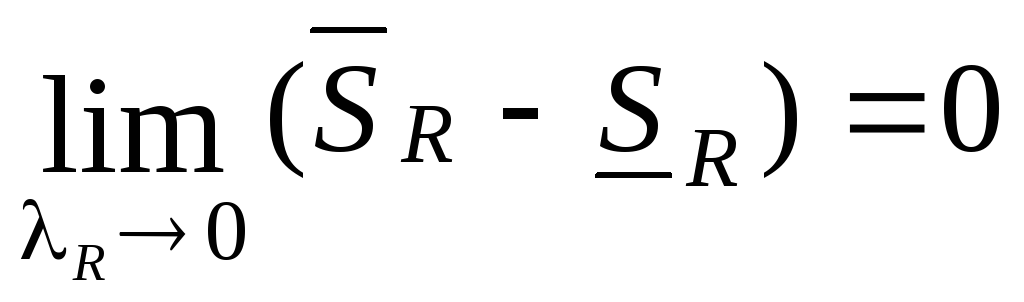 )
функция интегрируема тогда и только
тогда, когда
)
функция интегрируема тогда и только
тогда, когда
 (1). Надо доказать, что если
(1). Надо доказать, что если![]() .
Т.е. если найдется одноR*,
удовлетворяющее неравенству (1), то оно
(неравенство) будет выполняться для
всех R.
Возьмем произвольное
.
Т.е. если найдется одноR*,
удовлетворяющее неравенству (1), то оно
(неравенство) будет выполняться для
всех R.
Возьмем произвольное
![]() .
Нужно найтиδ,
такое чтобы выполнялось неравенство
.
Нужно найтиδ,
такое чтобы выполнялось неравенство
![]() .
По условию теоремы
.
По условию теоремы![]() .
Рассмотрим наше разбиениеR*
и произвольное R,
как показано на рисунке. Составим
разность верхней и нижней сумм Дарбý
для нового разбиения R:
.
Рассмотрим наше разбиениеR*
и произвольное R,
как показано на рисунке. Составим
разность верхней и нижней сумм Дарбý
для нового разбиения R:
![]() .
Нужно сделать его меньше
.
Нужно сделать его меньше![]() .
Из условия имеем
.
Из условия имеем![]() .
Обозначим через Σ первую сумму и разобьем
ее: Σ=Σ1+Σ2.
Σ1 –
такие слагаемые, что элемент нового
разбиения R
содержит в себе хотя бы одну точку
границы старого разбиения R*.
Все остальное войдет в Σ2.
Рассмотрим отдельно Σ1
и Σ2:
.
Обозначим через Σ первую сумму и разобьем
ее: Σ=Σ1+Σ2.
Σ1 –
такие слагаемые, что элемент нового
разбиения R
содержит в себе хотя бы одну точку
границы старого разбиения R*.
Все остальное войдет в Σ2.
Рассмотрим отдельно Σ1
и Σ2:
Σ1:
![]() т.к. функцияf
– ограничена (k
- константа). Тогда
т.к. функцияf
– ограничена (k
- константа). Тогда
![]() (M
и m
– максимум и минимум на [a,b]).
Получим Σ1
(M
и m
– максимум и минимум на [a,b]).
Получим Σ1![]() ,
гдеλR<δ,
а количество красных отрезков не
превосходит 2n.
Для того чтобы это неравенство выполнялось,
достаточно взять δ<
,
гдеλR<δ,
а количество красных отрезков не
превосходит 2n.
Для того чтобы это неравенство выполнялось,
достаточно взять δ<![]() /8kn.
Т.е. при δ<
/8kn.
Т.е. при δ<![]() /8kn
Σ1<
/8kn
Σ1<![]() /2.
/2.
Σ2:
разобьем Σ2
на повторные суммы, т.е. Σ2=Σ(Σi).
Σi≤![]() ≤
≤![]() (Mi*-mi*)ΣΔxi*,
где Mj
и mj
– максимум и минимум на j-том
участке. Σi
– группировка тех новых j-тых
участков, которые попали в один и тот
же старый. Получим Σ2
(Mi*-mi*)ΣΔxi*,
где Mj
и mj
– максимум и минимум на j-том
участке. Σi
– группировка тех новых j-тых
участков, которые попали в один и тот
же старый. Получим Σ2![]() Σ1+Σ2<ε,
т.е. Σ<
Σ1+Σ2<ε,
т.е. Σ<![]() .
В итоге:
.
В итоге:
![]() .
Теорема доказана.
.
Теорема доказана.
Следствие
1:
Функция f
– интегрируема на [a,b],
если
![]() с
с![]() :
:![]() (если существует такая последовательность
разбиений с мелкостью, стремящейся к
нулю, что модуль разности последовательности
интегральных сумм и интеграла стремится
к нулю).
(если существует такая последовательность
разбиений с мелкостью, стремящейся к
нулю, что модуль разности последовательности
интегральных сумм и интеграла стремится
к нулю).
Следствие
2:
Функция f
– интегрируема на [a,b],
если
![]() (если
верхний интеграл равен нижнему).
(если
верхний интеграл равен нижнему).
