2 семестр МПиТК / 2-й семестр / Лекции Соколова / 2_6

Дифференцирование.

Частные производные и производные по направлению.

Пустьопределена в некоторой окрестности точки . Зададим приращение координате

Если существует , то он называется частной производной функции по в точке .

Это можно записать как , где , тогда можно рассмотреть функцию одной переменной . Тогда частная производная .

Пусть задана точка и какое-то приращение . Функция определена в окрестности точки , тогда можно рассматривать . Этот предел называется производной функции по направлению .

Тогда производную по направлению можно рассматривать как частную производную справа , то есть по положительному направлению оси . Слева аналогично.

Далее мы выводили, что если , то

Можно определить по индукции производную n-го порядка.

Если оказалось, что функция имеет производную по : , этот факт будет доказан позднее. Аналогично можно определить смешанную производную n - го порядка :.

Равенство смешанных производных.

Теорема 1. Пусть задана функция имеющая в некоторой точке непрерывные частные производные и , тогда они равны между собой.

Доказательство:

Обозначим

т.е. приращение придается переменной Аналогично,

Придадим приращение сначала переменной затем

Найдем

Далее придадим приращение сначала переменной затем

, то есть, мы получили, что приращения равны между собой.

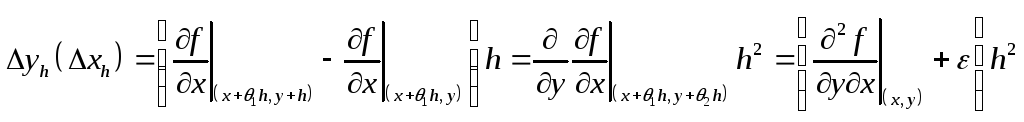- Вот момент, в котором мы пользовались непрерывностью смешанных производных.

;

Так как производные равны, то равны и их пределы.

Лекции 3-4.

Дифференцируемые функции. Касательная плоскость.

Рассмотрим частный случай, функцию трех переменных. Пусть задана функция f: - открытое множество. Пусть в некоторой точке функция f имеет непрерывные частные производные в некоторой окрестности точки . Т.к. эти производные непрерывны в точке , это означает, что все они существуют в некоторой окрестности точки . Зададим приращения таким образом, чтобы точка с координатами попала в ту окрестность, в которой функция имеет частные производные.

Рассмотрим приращение функции:

Теперь обозначим , тогда условие эквивалентно условию , потому что ранее было показано, что каждый куб содержится в шаре, каждый шар содержится в кубе, и условие .

Докажем, что :

при .

Доказано.

Итак мы получили, что если функция имеет непрерывные частные производные в точке , то ее приращение представимо в виде: , где частные производные вычислены в точке , т.е. не зависят от приращений.

Определение: Если задана f: - открытое множество, точка и если в этой точке приращение функции представимо в виде: , где не зависят от приращений , то функция f называется дифференцируемой в точке , а - дифференциал функции. Это главная линейная часть приращения функции. Линейная – потому что дифференциал линейно зависит от приращения аргумента, главная – потому что то, на что дифференциал отличается от приращения функции, имеет больший порядок малости.

Итак, мы доказали для случая 3-х переменных (для случая n переменных доказывается точно так же, только более громоздко), что если f имеет непрерывные частные производные, то она дифференцируема и . Кроме того, дифференциал можно рассматривать как линейный оператор:

возьмем в качестве A вектор , то , где .

Проведем теперь рассуждения в обратную сторону: пусть задана функция f, дифференцируемая в точке , тогда ее приращение представимо в виде: , где , в том числе по любому направлению. Возьмем в качестве приращения , тогда при .

Тогда получим, что

Разделим на и устремим к нулю, получим:

Слева – частная производная , справа - , т.е. .

Таким образом, мы получили, что если функция дифференцируема в точке с координатами , то она имеет частные производные первого порядка и дифференциал .

Мы доказали общую теорему:

Теорема (необходимое и достаточное условия дифференцируемости):

• Необходимое условие: если функция f дифференцируема в точке , то она имеет частные производные.

• Достаточное условие: если существуют непрерывные частные производные, то функция f дифференцируема.

Таким образом, получается следующая цепочка:

непрерывность ч.п. функция дифференцируема существуют частные производные

Ни в том, ни в другом месте стрелку в обратную сторону поставить нельзя, т.е. необходимое условие не является достаточным, достаточное не является необходимым. Для того, чтобы это доказать, приведем примеры.

Пример1

Покажем, что необходимое условие не является достаточным, т.е. что существует функция f , имеющая частные производные, но не являющаяся дифференцируемой. Как и в случае одной переменной, можно доказать, что если функция дифференцируема в точке, то она непрерывна в этой точке. Возьмем функцию, заданную следующим образом:

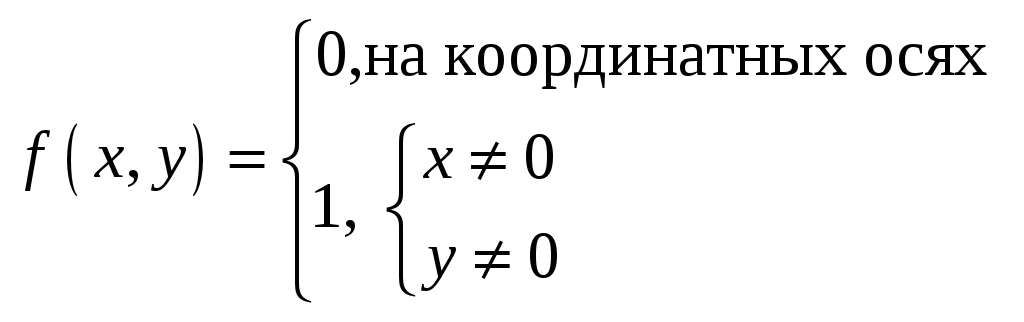
Тогда , т.к. мы приближаемся к точке (0,0) по оси, а значение функции на осях = 0. Однако функция в точке (0,0) разрывна, потому что в любой ее окрестности найдутся значения, равные как 0, так и 1, функция не дифференцируема.

Пример2

Покажем, что достаточное условие не является необходимым, т.е. что найдется функция f дифференцируемая, но не имеющая непрерывных частных производных.

Мы знаем, что если функция дифференцируема в точке, то она непрерывна в этой точке; это выполняется как для функций одной переменной, так и для функций нескольких переменных. Однако из того, что функция дифференцируема в точке не следует, что она непрерывна в некоторой окрестности этой точки.

Возьмем следующую функцию:

Рассмотрим дифференцируемость этой функции с точке (0,0):

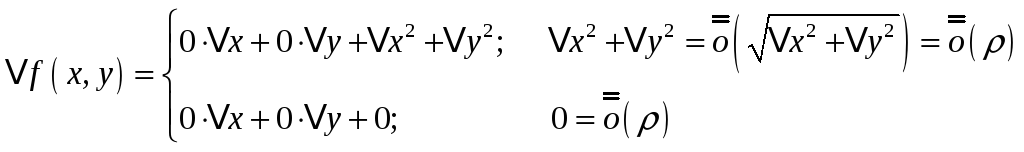
0 является от чего угодно, т.к. если мы 0 поделим на что угодно, то получим 0.

Таким образом, мы представили в виде:

Т.е. функция в точке (0,0) является дифференцируемой и дифференциал этой функции = 0.

Однако в остальных точках, кроме 0, эта функция разрывна, поэтому частных производных в этих точках не существует, тем более не имеет смысла говорить об их непрерывности. Т.е. получили, что функция дифференцируема в точке , но непрерывных частных производных нет.

Теорема доказана.

Касательная плоскость.

П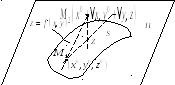усть f(x,y) дифференцируема в точке . Построим плоскость П: , где . Рассмотрим поверхность , точка с координатами принадлежит поверхности S. Плоскость П также проходит через точку . Возьмем произвольное приращение и рассмотрим точку Z с координатами , принадлежащую поверхности S. Рассмотрим соответствующую точку на плоскости , назовем эту точку . Измерим расстояние между точками Z и . Координаты x и y у этих точек одинаковы, значит расстояние между этими точками равно разности между их координатами z.

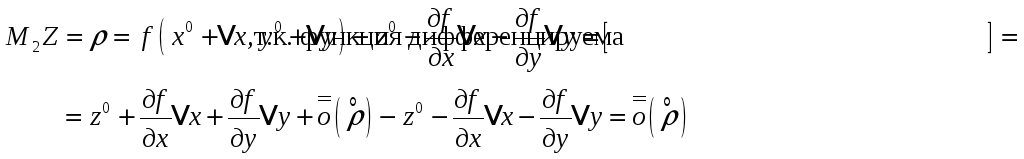
где , т.е. мы получили, что если функция f дифференцируема и мы построили такую плоскость, то расстояние от этой плоскости до поверхности вдоль оси z стремится к нулю быстрее, чем расстояние между точками на плоскости. Плоскость, обладающая таким свойством, называется касательной.

Определение: Пусть заданы поверхность ; ; и П – плоскость, проходящая через точку . Если расстояние между П и S, измеренное вдоль оси z, при стремится к нулю быстрее, чем , то такая плоскость называется касательной.

В обратную сторону рассуждения тоже верны:

Если плоскость является касательной, то функция f - дифференцируема, при этом .

Производная сложной функции и производная по направлению. Градиент.

Рассмотрим для удобства записи функцию трех переменных, т.к. случай трех переменных легко распространяются на n.

Пусть f(x,y,z) дифференцируема в точке . Пусть , где дифференцируемы в точке , причем , тогда можно рассмотреть функцию - функция одной переменной. Эта функция будет дифференцируема в точке .

- т.к. функция дифференцируема по условию.

Когда мы устремляем к нулю, стремится к , и т.д, остается только доказать, что .

Таким образом, устремив к нулю, получаем:

Пример:

Найдем производную функции , рассматривая ее как функцию двух переменных, без логарифмирования.

Рассмотрим функцию , где , тогда , будем считать ее производную как производную сложной функции:

Меняем x и y обратно на t:

Пусть задана функция , где . Пусть существуют непрерывные частные производные . В свою очередь , где , имеющие частные производные - тоже непрерывные, тогда - дифференцируема и ее частные производные будут равны .

Рассмотрим приращение функции вдоль переменной на вектор .

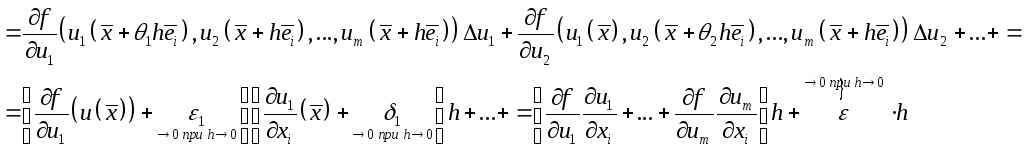
бесконечно малая функция. Так как наша функция имеет частную производную, то, - непрерывны , значит, при .

Пример. Пусть задана функция , где .

Конечно, можно эти функции подставить и посчитать, ничего сложного, но можно сделать и через частные производные: