
Модуль4.
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ.
Лекции 1-2
Предел и непрерывность.
Основные понятия.
Рассмотрим
пространство
![]() множество
точек
множество
точек
![]() с координатами
с координатами
![]() .
Расстоянием между двумя точками
.
Расстоянием между двумя точками
![]() называется
называется
![]() - это евклидово расстояние между двумя
точками.
- это евклидово расстояние между двумя
точками.
Назовем замкнутым
шаром с центром в точке
![]() и радиусом
и радиусом
![]() множество точек
множество точек
![]() .
.
Открытый шар с
центром в точке
![]() и радиусом
и радиусом
![]() - множество точек
- множество точек
![]()
Замкнутым кубом
с центром в точке
![]() и стороной
и стороной
![]() называют множество точек
называют множество точек
![]()
Открытым кубом с
центром в точке
![]() и стороной
и стороной
![]() называют множество точек
называют множество точек
![]()
В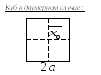 ажно,
что если мы возьмем шар с центром в точке
ажно,
что если мы возьмем шар с центром в точке
![]() и радиусом
и радиусом
![]() ,
то он всегда будет содержаться в кубе
с центром в точке
,
то он всегда будет содержаться в кубе
с центром в точке
![]() и стороной
и стороной
![]() .
.
![]() ,
,
![]()
Доказательство:
Возьмем произвольную
точку
![]() ,
тогда
,
тогда
![]() выполняется неравенство:
выполняется неравенство:
![]() - по определению
- по определению
![]() шара.
Мы хотим доказать, что
шара.
Мы хотим доказать, что
![]() ,
т.е.
,
т.е.
![]() .
Действительно,
.
Действительно,
![]() ,
т.к.
,
т.к.
![]() ,
значит
,
значит
![]() ,
т.к. выполняется неравенство для куба.
,
т.к. выполняется неравенство для куба.
Утверждение доказано.
Теперь возьмем
![]() ,
тогда
,
тогда
![]() .
Мы хотим поместить этот куб в какой-то
шар, тогда получим:
.
Мы хотим поместить этот куб в какой-то
шар, тогда получим:
![]() ,
т.к.
,
т.к.
![]() - по определению куба; n
– размерность пространства. Тогда точка
- по определению куба; n
– размерность пространства. Тогда точка
![]() ,
которую мы взяли, будет принадлежать
шару:
,
которую мы взяли, будет принадлежать
шару:
![]() - радиус шара, в который можно вписать
куб.
- радиус шара, в который можно вписать
куб.
Получаем цепочку
включений:
![]() .
Аналогичное включение можно записать
для открытых шаров и кубов.
.
Аналогичное включение можно записать
для открытых шаров и кубов.
Это нужно нам для того, чтобы в дальнейшем говорить, что принадлежность шару эквивалентна принадлежности кубу и наоборот – ввиду этих неравенств.
Определение:
Множество
![]() называется открытым, если любая точка
принадлежит ему вместе с некоторым
открытым шаром (можно сказать, что и
вместе с некоторым замкнутым шаром,
потому что если точка содержится с
некоторым открытым шаром, то возьмем
замкнутый шар с радиусом, допустим, в
два раза меньше радиуса открытого шара,
и он тоже будет принадлежать этому
множеству).
называется открытым, если любая точка
принадлежит ему вместе с некоторым
открытым шаром (можно сказать, что и
вместе с некоторым замкнутым шаром,
потому что если точка содержится с
некоторым открытым шаром, то возьмем
замкнутый шар с радиусом, допустим, в
два раза меньше радиуса открытого шара,
и он тоже будет принадлежать этому
множеству).
![]() - определение
открытого множества.
- определение
открытого множества.
П римеры:
римеры:
![]()
![]() ;
;
Доказательство:
Возьмем произвольную
точку
![]() из открытого шара: тогда
из открытого шара: тогда
![]()
![]() .
Возьмем
.
Возьмем
![]() ,
тогда
,
тогда
рассмотрим шар с
центром в точке
![]() и радиусом
и радиусом
![]()
![]() :
тогда
:
тогда
![]()
![]() ,
т.е. любая точка, принадлежащая маленькому
шару, принадлежит и большому шару.
,
т.е. любая точка, принадлежащая маленькому
шару, принадлежит и большому шару.
Пояснение:
т.к.
![]() ,
,
![]() .
А мы брали
.
А мы брали
![]() ,
поэтому
,
поэтому
![]() , а значит и
, а значит и
![]()
 .
.
4)
![]()
Действительно,
если мы возьмем точку
![]() такую, что
такую, что
![]() ,
то
,
то
![]()
Определение:
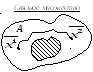 Множество
Множество
![]() называется связным, если
называется связным, если
![]() найдется непрерывная кривая, лежащая
в
найдется непрерывная кривая, лежащая
в
![]() ,
соединяющая точки
,
соединяющая точки
![]() .
.
Т.е. найдется n
функций
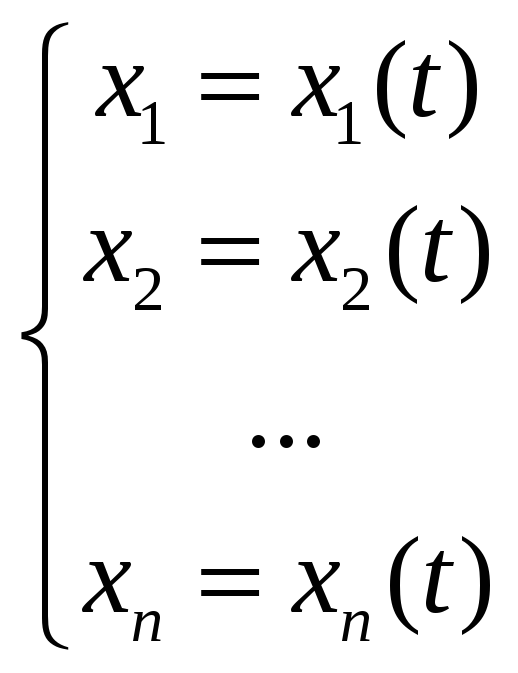 такие, что кривая
такие, что кривая
![]() задается уравнением:
задается уравнением:
![]()
![]() ,
,
![]() и
эти функции непрерывны на
и
эти функции непрерывны на
![]() .
.
Определение:
Множество
![]() называется односвязным, если мы возьмем
любую замкнутую кривую в этом множестве,
будем стягивать ее в точку и все равно
при этом оставаться в этом множестве
(множество, приведенное для примера
связного множества, не является
односвязным).
называется односвязным, если мы возьмем
любую замкнутую кривую в этом множестве,
будем стягивать ее в точку и все равно
при этом оставаться в этом множестве
(множество, приведенное для примера
связного множества, не является
односвязным).
Определение:
Отрезком, соединяющим точки
![]() ,
называются такое множество точек
,
называются такое множество точек
![]()
Определение:
Множество называется выпуклым, если
![]() .
.
Пример:
Промежуток на
![]() - это отрезок, интервал, полуинтервал,
луч, открытый луч, вся числовая прямая.
Можно сказать, что промежутком на
- это отрезок, интервал, полуинтервал,
луч, открытый луч, вся числовая прямая.
Можно сказать, что промежутком на
![]() называют всякое выпуклое множество,
или что промежутком на
называют всякое выпуклое множество,
или что промежутком на
![]() называют всякое связное множество.
называют всякое связное множество.
Предел последовательности.
Определение1:
Последовательность точек
![]() ,
если
,
если
![]() .
.
Определение2:
Последовательность точек
![]() ,
если
,
если
![]() .
.
Утверждение: Определения 1 и 2 эквивалентны.
Доказательство:
![]() Возьмем по
определению1
Возьмем по
определению1
![]() ,
это означает, что
,
это означает, что
![]() ,
,
тогда
![]() ,
т.е. выполняется определение2.
,
т.е. выполняется определение2.
Доказано.
![]() Пусть по определению2
Пусть по определению2
![]() ,
т.е.
,
т.е.
![]() ,
тогда
,
тогда
![]() ,
тогда возьмем
,
тогда возьмем
![]() ,
и тогда
,
и тогда
![]() ,
т.е. точка
,
т.е. точка
![]() ,
т.е. для точки
,
т.е. для точки
![]() выполняется неравенство:
выполняется неравенство:
![]() ,
что соответствует определению1.
,
что соответствует определению1.
Утверждение доказано.
Тот факт, что
определение 1 эквивалентно определению
2 можно выразить еще так: последовательность
точек
![]() стремится к точке
стремится к точке
![]() ,
когда есть покоординатная сходимость.
,
когда есть покоординатная сходимость.
Определение3:
Последовательность точек
![]() называется ограниченной, если она
содержится в некотором кубе (шаре),
замкнутом или открытом. Причем можно
считать, что она содержится в шаре или
кубе с центром в начале координат.
называется ограниченной, если она
содержится в некотором кубе (шаре),
замкнутом или открытом. Причем можно
считать, что она содержится в шаре или
кубе с центром в начале координат.
Действительно,
если
![]() то
она содержится и в
то
она содержится и в
![]() :
:
![]()
Теорема Больцано-Вейерштрасса:
Из всякой ограниченной последовательности можно извлечь сходящуюся подпоследовательность.
Доказательство:
Пусть последовательность
![]() ограничена:
ограничена:![]() ,
тогда
,
тогда
![]() тоже
ограничена, потому что
тоже
ограничена, потому что
![]() .
.
Сначала извлекаем
сходящуюся последовательность из
последовательности
![]() :
она ограничена, поэтому из нее можно
извлечь сходящуюся подпоследовательность:
:
она ограничена, поэтому из нее можно
извлечь сходящуюся подпоследовательность:![]() .
Теперь рассмотрим подпоследовательность
второй координаты
.
Теперь рассмотрим подпоследовательность
второй координаты
![]() :
она тоже является ограниченной, значит
из нее можно извлечь сходящуюся
подпоследовательность
:
она тоже является ограниченной, значит
из нее можно извлечь сходящуюся
подпоследовательность
![]() ,
при этом последовательность
,
при этом последовательность
![]() осталась сходящейся, потому что
осталась сходящейся, потому что
![]() - подпоследовательность
- подпоследовательность
![]() ,
и т.д. Т.е. когда мы получили
подпоследовательность
,
и т.д. Т.е. когда мы получили
подпоследовательность
![]() ,
то она будет сходящейся, и все остальные
последовательности координат тоже при
этом остаются сходящимися. Значит, и
,
то она будет сходящейся, и все остальные
последовательности координат тоже при
этом остаются сходящимися. Значит, и
![]() - тоже сходится, т.к. есть покоординатная
сходимость.
- тоже сходится, т.к. есть покоординатная
сходимость.
Теорема доказана.
Определение4:
![]() – предельная точка множества
– предельная точка множества
![]() ,
если существует последовательность
,
если существует последовательность
![]() точек из множества А,
сходящаяся
к точке
точек из множества А,
сходящаяся
к точке
![]() и
и
![]() ,
т.е. если
,
т.е. если
![]() .
.
Предельная точка может принадлежать множеству А, а может и не принадлежать.
Пример: У открытого шара множество предельных точек – замкнутый шар, у замкнутого шара – тоже замкнутый шар.
Определение5: Объединение множества и его предельных точек называется замыканием.
Пример:
Замыкание
открытого шара
![]() - замкнутый шар
- замкнутый шар
![]() - ставим черточку сверху при замыкании.
- ставим черточку сверху при замыкании.
![]()
Определение6:
Множество
![]() называется замкнутым, если оно совпадает
со своим замыканием, т.е. все его предельные
точки ему принадлежат.
называется замкнутым, если оно совпадает
со своим замыканием, т.е. все его предельные
точки ему принадлежат.
Примеры:
![]() (из того, что точка принадлежит множеству
следует, что должна существовать
последовательность точек множества,
сходящаяся к ней, а этому множеству
ничего не принадлежит);
(из того, что точка принадлежит множеству
следует, что должна существовать
последовательность точек множества,
сходящаяся к ней, а этому множеству
ничего не принадлежит);
![]() ;
;
Теорема (связь между открытыми и замкнутыми множествами):
Если А
– замкнутое,
то
![]() - открытое
- открытое
![]() .
.
Если А
– открытое,
то
![]() - замкнутое.
- замкнутое.
Доказательство:
Доказывать только один пункт не достаточно, потому что существуют множества, не являющиеся ни открытыми, ни замкнутыми.
1. Пусть А – замкнутое, тогда
предположим, что
![]() не является открытым, построим отрицание
к определению открытого множества:
не является открытым, построим отрицание
к определению открытого множества:

![]()
Если точка не
принадлежит
![]() ,
то она принадлежит А,
но это есть определение предельной
точки: само
,
то она принадлежит А,
но это есть определение предельной
точки: само
![]() не принадлежит множеству А,
но в любой его окрестности найдутся
точки из А:
не принадлежит множеству А,
но в любой его окрестности найдутся
точки из А:
![]() предельная
точка для множества
предельная
точка для множества
![]() ,
а
,
а
![]() - замкнутое, значит
- замкнутое, значит
![]() .
Пришли к противоречию, которое получилось
из предположения, что множество А
не является открытым.
.
Пришли к противоречию, которое получилось
из предположения, что множество А
не является открытым.
Первый пункт доказан.
2. Пусть А – открытое, тогда
рассмотрим множество
![]() :
возьмем произвольную точку
:
возьмем произвольную точку
![]() .
Мы хотим доказать, что это множество
является замкнутым, т.е. содержит все
свои предельные точки. Предположим
обратное: пусть множество A
содержит в себе не все свои предельные
точки. Тогда пусть
.
Мы хотим доказать, что это множество
является замкнутым, т.е. содержит все
свои предельные точки. Предположим
обратное: пусть множество A
содержит в себе не все свои предельные
точки. Тогда пусть
![]() не является замкнутым, это означает,
что
не является замкнутым, это означает,
что
![]() предельная
точка для
предельная
точка для
![]() ,
но
,
но
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() ,
а A
– открытое
множество, значит
,
а A
– открытое
множество, значит
![]() принадлежит А
вместе с некоторой окрестностью, т.е.
принадлежит А
вместе с некоторой окрестностью, т.е.
![]() .
Но тогда мы не можем приблизиться к
точке
.
Но тогда мы не можем приблизиться к
точке
![]() по точкам множества
по точкам множества
![]() ,
потому что, т.к. эта точка предельная,
существует последовательность
,
потому что, т.к. эта точка предельная,
существует последовательность
![]() ,
такая что
,
такая что
![]() ,
т.е. мы получили, что в любой окрестности
точки
,
т.е. мы получили, что в любой окрестности
точки
![]() есть элементы множества
есть элементы множества
![]() .
А ранее было доказано, что найдется
окрестность, в которой нет элементов
.
А ранее было доказано, что найдется
окрестность, в которой нет элементов
![]() .
Пришли к противоречию.
.
Пришли к противоречию.
Теорема доказана.
