Лекция 15 . Несобственные интегралы. Понятие о несобственных интегралах.

Пусть задана функция интегрируема на. Тогда еслии он конечен, то говорим, чтосходится и равен пределу. Обычный интеграл Римана называется собственным интегралом, а пределназывается несобственным интегралом. Мы вводим это новое понятие, поскольку в смысле Римана не существует интеграла на бесконечном отрезке, однако может существовать несобственный интеграл, равный. Аналогично определяется .

Пример:

Р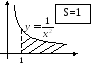ассмотрим интеграл:

Мы получили, что площадь бесконечной фигуры = 1, где площадь мы не

можем определить через вписанные и описанные фигуры, но зато площадь вписанных фигур стремится к 1. Если первообразнаянаи, то допустима запись. Т.е. это интеграл с особенностью на бесконечности.

Рассмотрим на конечномпустьфункция интегрируема на отрезкеи неограниченна в левой окрестности точкиb. Тогда в обычном смысле Римана интеграл не существует (по теореме об ограниченности интегрируемой функции). Однако может . И если этот предел существует, то говорим, что несобственный интеграл сходится, и. Аналогично, если все точно так же, но слева (на). Если эти пределы в обоих случаях не существуют или, то несобственный интеграл называется расходящимся.

Пример:

Рассмотрим интеграл :функция интегрируема на отрезке, и сама функция неограниченна в окрестности нуля. Тогда можно говорить о несобственном интеграле.

, т.е. интеграл расходится.

Дадим определение особенности. Пусть f(x) задана на полуинтервале [a,b), где b – или конечное, или бесконечное. Будем говорить, что интеграл имеет единственную особенность в точке b, если интегрируема на, причем

• если 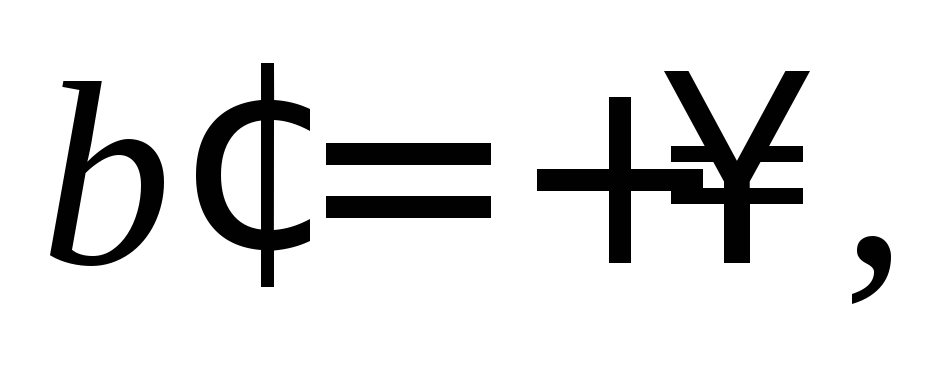то больше ничего не требуется;

• если 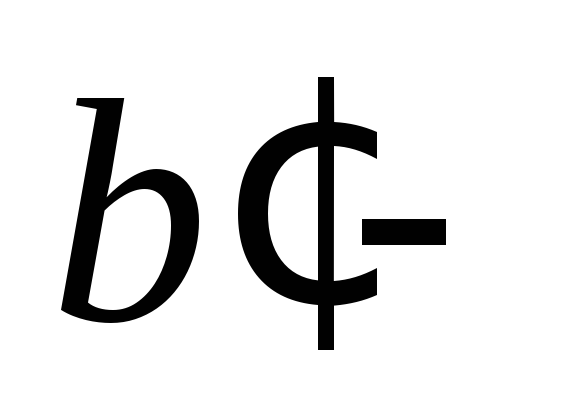конечно, тоf – неограниченна в левой окрестности точки b.

Аналогично определяется единственная особенность в точке a.

Дадим определение интеграла с несколькими особенностями:

Рассмотрим функцию f, заданную на отрезке , a,b – конечны.

Будем говорить, что интеграл функции f имеет особенности в точках , еслиинтегралыимеют единственную особенность. Можно еще это определение переформулировать следующим образом. Зададимf на интервале : тогда еслиимеют единственную особенность, первый – в точкеa, второй – в точке b, и оба являются сходящимися, то считаем, что сходится, и его значение:

Нужно доказать, что это равенство выполняется для любого c (провести доказательство корректности).

Доказательство:

Пусть - сходящиеся. Тогда рассмотрим сумму:

Корректность доказана. Какую бы точку мы не взяли из интервала, сумма интегралов будет одна и та же. Таким образом, мы определили интеграл с особенностями на обоих концах. Тогда можно по-другому определить сходимость интеграла с особенностью в нескольких точках:

Пусть f задана на , а точкитаковы, чтоимеют не более двух особенностей, причем на концах. Тогдаимеет несколько особенностей и называется сходящимся, если сходится каждый из тех интегралов, и

Пример:

, последний интеграл расходится, значит и первоначальный интеграл тоже расходится.

Свойства несобственных интегралов.

Теорема 1 (Условие Коши)

с единственной особенностью в точке b (конечной или бесконечной) сходится тогда и только тогда, когда:

Мы имеем право писать последний интеграл как раз потому, что он имеет особенность только в точке b, а в точках все в порядке.

Доказательство:

Рассмотрим функцию:

Т.е. из того, что интеграл сходится, следует, что существует предел функции F(x), а из этого следует, что для этой функции выполняется условие Коши.

Теорема доказана.

Теорема 2 (Аддитивное свойство несобственных интегралов):

Пусть имеет единственную особенность в точкеb и сходится, тогда

тоже имеет единственную особенность в точке b и тоже сходится, при этом

Доказательство:

Условие Коши для интегралов ивыглядит одинаково, поэтому интегралсходится.

Проверка равенства:

Таким образом, получили аддитивное свойство и для несобственных интегралов:

. Это равенство выполняется независимо от того, собственный он или несобственный, важно только, чтобы он был сходящимся.

Теорема доказана.

Теорема 3 (Однородное свойство для несобственных интегралов):

Пусть имеет единственную особенность в точкеb и сходится, также имеет единственную особенность в точкеb и сходится. Тогда и имеет единственную особенность в точкеb, сходится и равен .

Доказательство:

Теорема доказана.

Важные примеры (их результат нужно запомнить):

1. 

а) - интеграл расходится

б)

Значит,

2. 

а) - интеграл расходится

б)

Значит,