2 семестр МПиТК / 2-й семестр / Коллоквиум 2 поток / Коллоквиум

Конспект лекций для подготовки к коллоквиуму (МП-16,17,17а,18,19)

Несобственные интегралы.

Интеграл Римана был введен для ограниченных на отрезке функций. Естественно распространить понятие интеграла на случай бесконечного промежутка, а также на случай, когда подынтегральная функция является неограниченной.

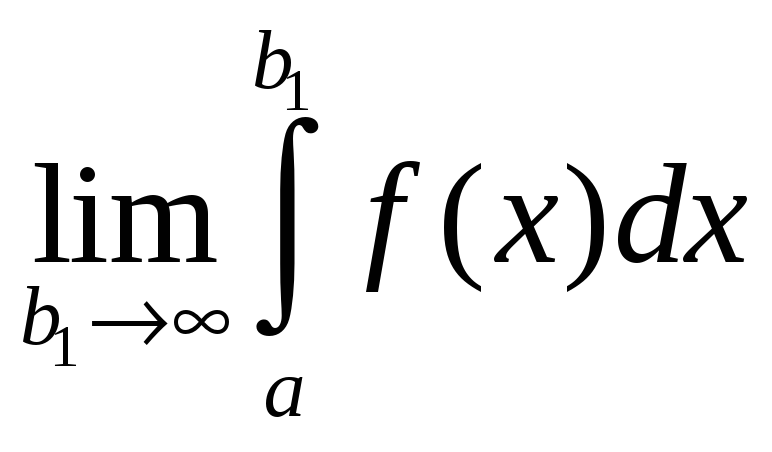Опр. Пусть задана на луче и интегрируема на любом конечном отрезке . Если существует предел , то он называется несобственным интегралом первого рода и обозначается .

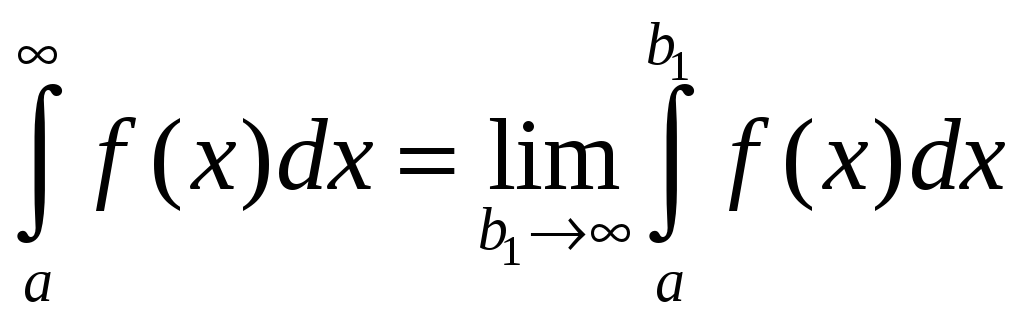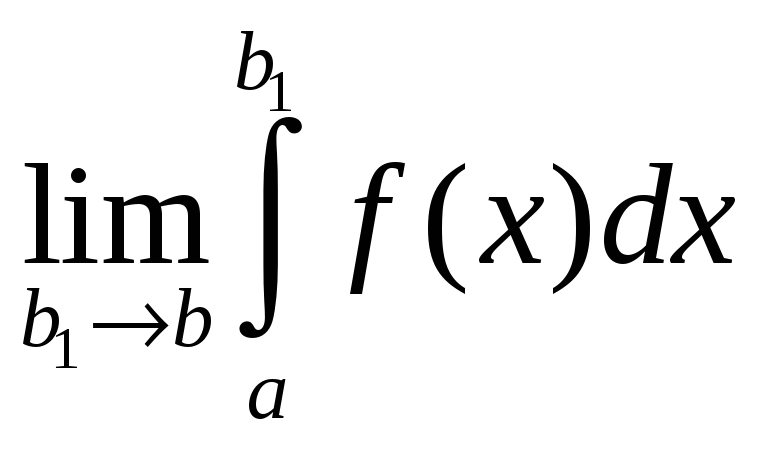Опр. Пусть задана на полуинтервале , интегрируема на любом конечном отрезке , и неограниченна в окрестности точки . Если существует предел , то он называется несобственным интегралом второго рода и обозначается .

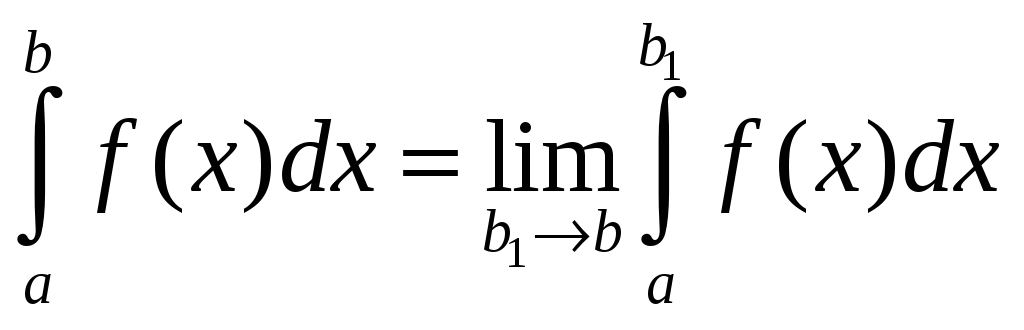Если указанные пределы конечные, то интегралы называются сходящимися, если бесконечные, то расходящимися, если пределы не существуют, то, говорят, что несобственные интегралы не существуют.

Замечание. Определение несобственного интеграла на полуинтервале является содержательным лишь при неограниченности функции в окрестности точки . Действительно, если определена и ограничена на , то доопределив в точке , получим интегрируемую на функцию. При этом интеграл не зависит от значения функции в одной точке .

Теор. (Критерий Коши сходимости несобственных интегралов) Пусть задан интеграл с единственной особенностью в точке ( неограниченна в точке или ). Для его сходимости необходимо и достаточно выполнения условия Коши: .

Док. Рассмотрим функцию Тогда сходимость интеграла означает существование конечного предела функции при , а этот конечный предел, согласно Критерию Коши для функции , существует в том и только том случае, когда удовлетворяет условию: . Но . Теорема доказана.

Свойства несобственных интегралов.

1. и , особенность в точке - сходятся и расходятся одновременно. (Критерий Коши формулируется одинаково).

2. =+.

(Является следствием равенства =+).

3. Если - сходится, то сходится , причем .

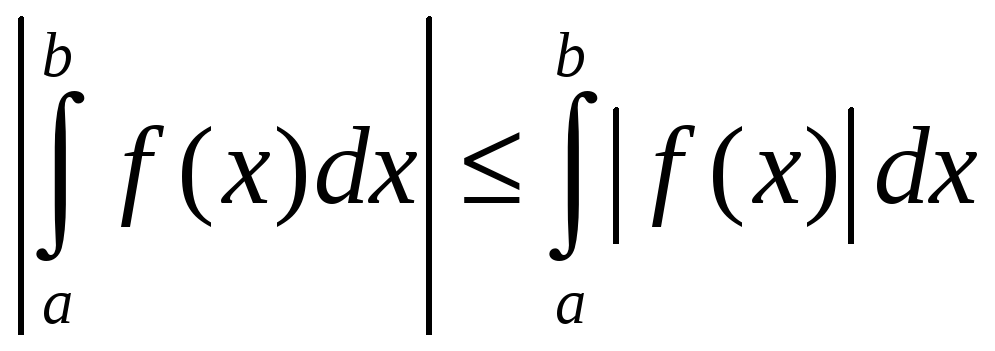( Из условия Коши сходимости интеграла следует условие Коши для интеграла , т.к. справедливо неравенство 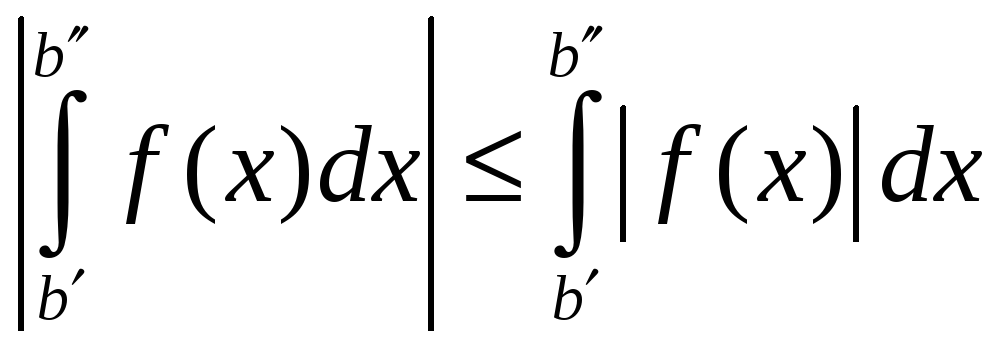. Воспользуемся неравенством 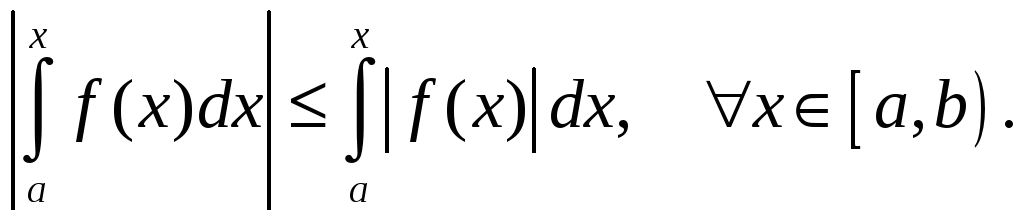В силу сходимости интегралов существуют пределы от левой и правой частей. Переходя к пределам, получаем неравенство .)

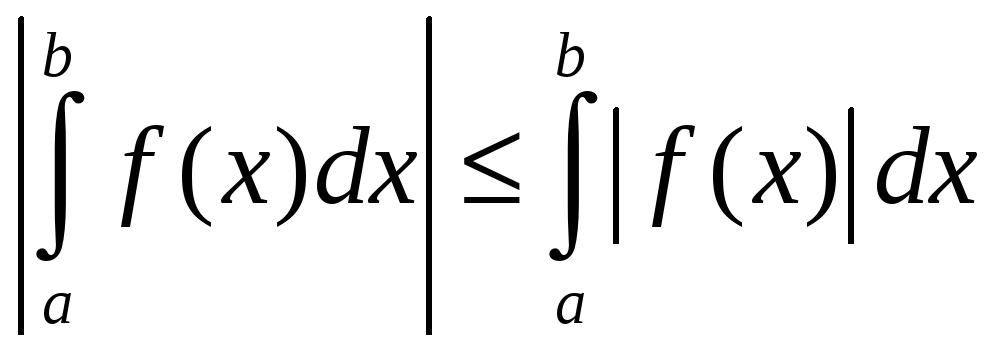Несобственные интегралы от неотрицательных функций.

Теор. Если , то для сходимости необходимо и достаточно, чтобы функция бала ограничена сверху, т.е. .

Док. Так как возрастающая функция, то из сходимости интеграла следует Обратно, если возрастающая функция и ограничена сверху, то она имеет конечный предел. Теорема доказана.

Теор. (Признак сравнения). Если выполняется условие , тогда:

а). Из сходимости следует сходимость ;

б). Из расходимости следует расходимость .

Док. а). Имеем Так как , то по предыдущей теореме сходится.

б). Из расходимости следует расходимость . Предположим обратное, что сходится, тогда по пункту а) тоже сходится. Противоречие. Теорема доказана.

Теор. (Предельный признак сравнения). Пусть функции и положительны и , тогда несобственные интегралы и сходятся и расходятся одновременно.

Док. . Раскрывая последнее неравенство и используя признак сравнения, получим, что интегралы и сходятся и расходятся одновременно. Теорема доказана.

Интегрирование по частям несобственных интегралов.

Пример. Показать, что сходится.

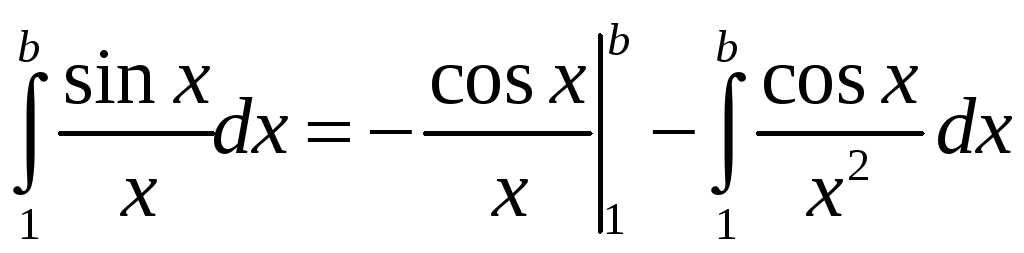. Переходим к пределу . Последний интеграл сходится абсолютно, т.к. сходится интеграл от модуля функции .

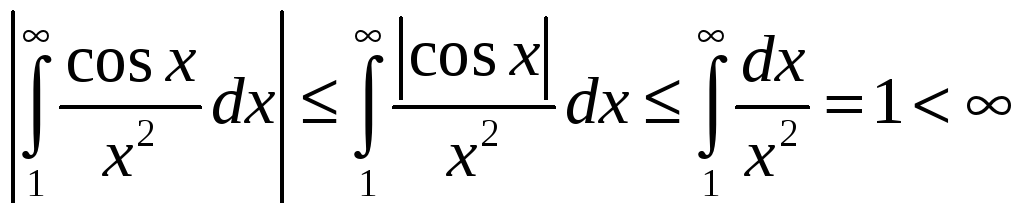Аналогично показывают, что тоже сходится.

Пример. Показать, что сходится не абсолютно (условно).

. Первый из последних двух интегралов расходится, второй – сходится, значит, их разность расходится.

Функции многих переменных.

Опр. Точкой мерного пространства называется упорядоченная совокупность вещественных чисел . Число называется той координатой точки .

Опр. Пространством называется совокупность точек мерного пространства, расстояние между которыми определяется равенством .

Расстояние обладает свойствами:

1. ;

2. ;

3. .

Опр. окрестностью точки называется совокупность точек , удовлетворяющих неравенству . Обозначается .

Опр. Прямоугольной окрестностью точки называется совокупность точек , удовлетворяющих неравенствам . .

Утверждение. Какова бы ни была , существует , такая, что , и, наоборот, какова бы ни была , существует, такая, что .

Опр. Говорят, что на множестве задана последовательность , если каждому натуральному поставлена в соответствие точка .(Не обязательно разные точки для разных ).

Опр. Точка называется пределом последовательности , если .

Утверждение. Для того чтобы сходилась к точке , необходимо и достаточно, чтобы .

Открытое множество.

Пусть - некоторое множество точек в пространстве .

Опр. Точка называется внутренней точкой, если существует окрестность точки , содержащаяся в множестве .

Опр. Множество называется открытым, если все его точки внутренние.

Опр. Точка называется граничной точкой множества, если в любой окрестности этой точки существуют точки, как принадлежащие множеству, так и не принадлежащие множеству.

Опр. Множество называется ограниченным, если существует мерный шар с центром в начале координат, такой, что .

Опр. Множество называется связным, если любые две его точки можно соединить непрерывной прямой, принадлежащей этому множеству.

Опр. Областью называется открытое связное множество.

Предел и непрерывность функции.

Говорят, что на множестве задана функция , если каждой точке поставлено в соответствие действительное число .

Опр. , если определена в некоторой окрестности точки , за исключением быть может самой этой точки, и если .

Опр. (По Гейне) , если .

Опр. Функция непрерывна в точке , если она определена в некоторой окрестности точки и в самой этой точке, и если , то есть .

Частные производные.

.

Этот предел, если он существует, называется частной производной функции .

Дифференцируемость функции многих переменных.

Опр. Функция называется дифференцируемой в точке , если ее приращение можно представить в виде ,

где: - не зависит от ; при ; ; .

Теор. (Необходимое условие дифференцируемости). Если функция дифференцируема в точке , тогда она имеет в этой точке все частные производные.

Док. Пусть дифференцируема в точке , то есть . Пусть . Тогда , . Следовательно существует предел . Аналогично доказывается для .

Теор. (Достаточное условие дифференцируемости). Если все частные производные определены в окрестности точки и непрерывны в ней, тогда дифференцируема в точке .

Док. Рассмотрим приращение функции двух переменных. .

Используя два раза теорему Лагранжа о среднем и непрерывность частных производных, последнее выражение представим в виде .

Здесь: при .

Раскрывая скобки и группируя слагаемые, имеем .

при .

Таким образом, приращение функции представлено в виде , где - являются частными производными и не зависят от и . Теорема доказана.

Замечание. Непрерывность частных производных не является необходимым условием дифференцируемости. Рассмотрим функцию двух переменных

.

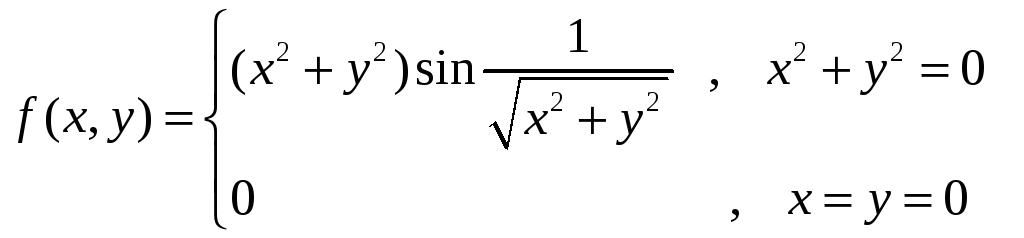Функция дифференцируема в точке , так как .

Частная производная не имеет предела при и, следовательно, не является непрерывной в точке .

Теор. (Необходимое и достаточное условие дифференцируемости). Функция дифференцируема в точке тогда и только тогда, когда в некоторой окрестности точки ее можно представить в виде: , где - некоторые непрерывные в точке функции.

Док. Из дифференцируемости имеем . Так как . Доопределив функцию в точке нулем, получим непрерывную функцию . Таким образом, имеем .

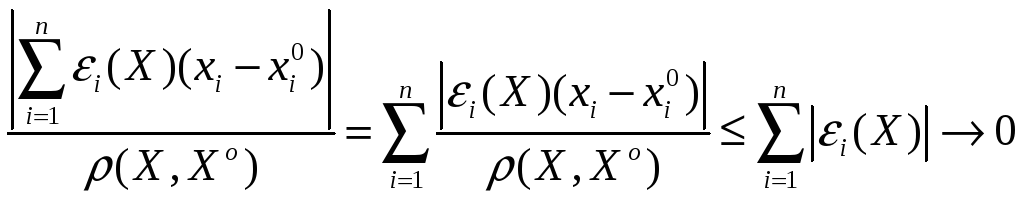Обратно, из равенства в формулировке теоремы, используя непрерывность функций в точке , т.е. , получаем . Действительно при . Теорема доказана.

Дифференцирование сложной функции.

Теор. Пусть дифференцированы в точке и функция дифференцируема в точке . Тогда сложная функция дифференцированы в точке , причем , где: ; .

Док. Имеем . Так как некие непрерывные функции, тогда тоже непрерывная функция, а значит дифференцируема. В силу равенств 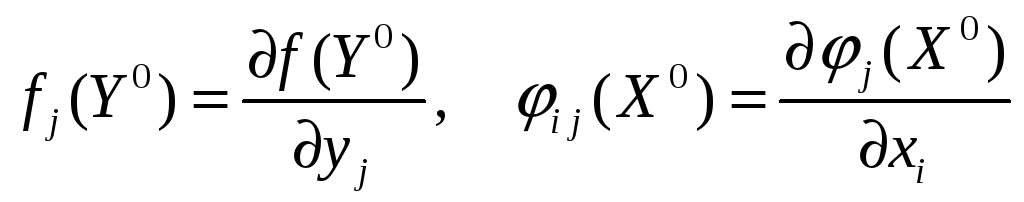частную производную можно записать в виде 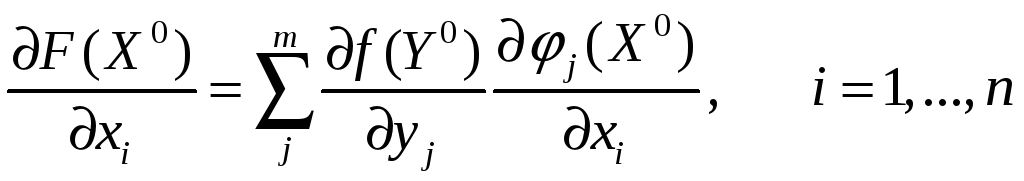. Теорема доказана.

Дифференциал. Инвариантность формы первого дифференциала.

Опр. Пусть дифференцируема в точке , тогда линейная относительно часть приращения этой функции называется дифференциалом .

Найдем дифференциал сложной функции .

.

Таким образом, форма записи первого дифференциала не зависит от того, зависимыми или независимыми являются переменные.

Геометрический смысл дифференциала. Касательная плоскость к графику функции двух переменных. Вектор нормали к ней.

- дифференциал.

- уравнение касательной плоскости.

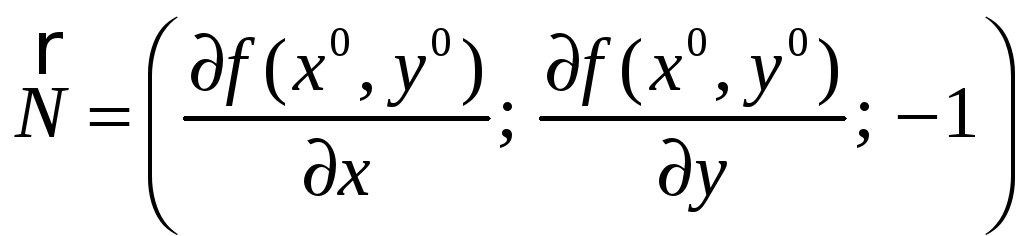- вектор нормали.

Частные производные и дифференциалы высших порядков.

Продифференцировав частные производные первого порядка по или по , получим производные второго порядка: ; ; ; .

Теор. (О смешанных производных). Пусть определена вместе со своими частными производными в некоторой окрестности точки , причем и непрерывны в этой точке, тогда .

Док. - приращение функции по переменной . Возьмем от приращения функции по приращение по . Последнее выражение можно рассматривать как приращение вспомогательной функции по переменной , поэтому, применяя к этому приращению теорему о среднем Лагранжа, получим . К выражению в квадратных скобках снова применим теорему Лагранжа как к приращению функции по переменной и получим . Аналогично . Приравниваем полученные выражения и переходим к пределу при . Учитывая непрерывность производных и , получим требуемое равенство . Теорема доказана.