1. Несобственные интегралы. Критерий Коши сходимости несобственных интегралов

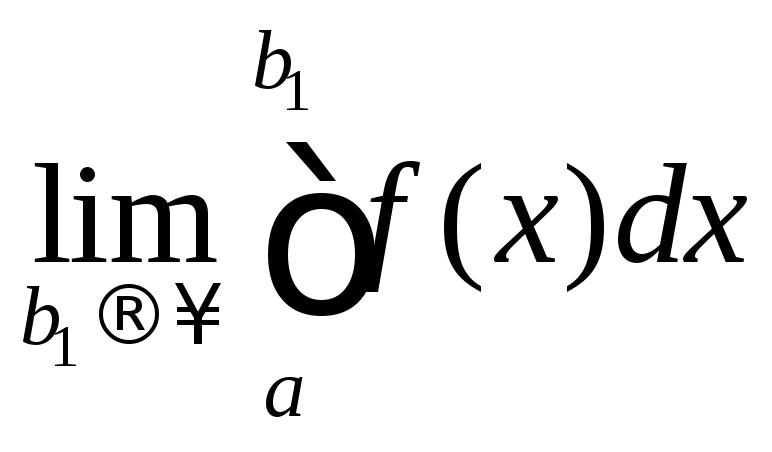Опр.Пустьзадана на лучеи интегрируема на любом конечном отрезке. Если существует предел, то он называется несобственным интегралом первого рода и обозначается.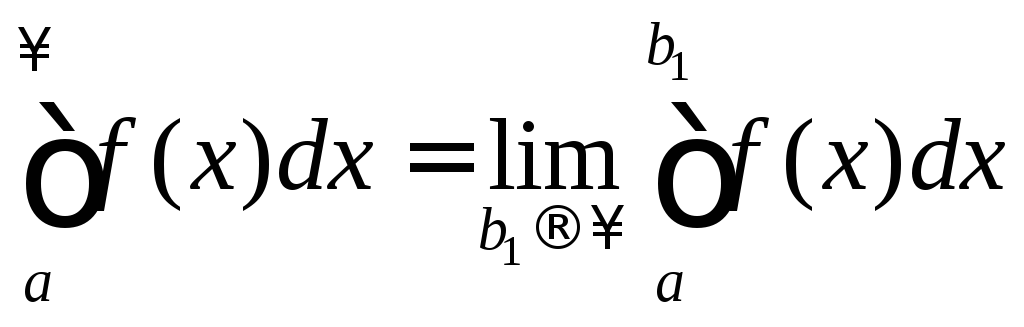

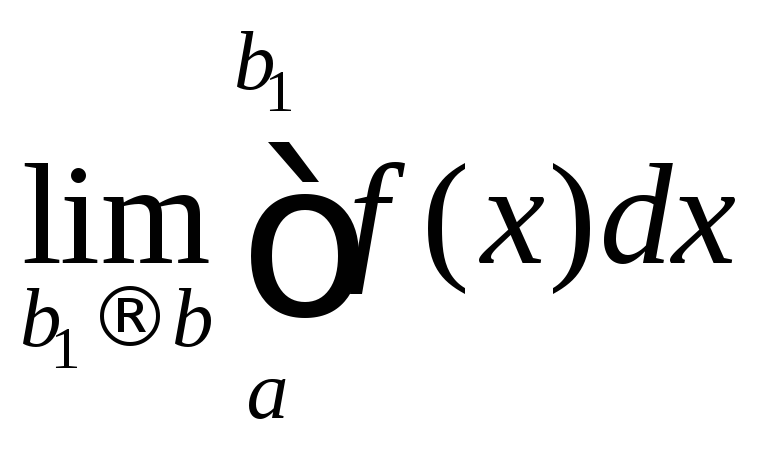Опр.Пустьзадана на полуинтервале, интегрируема на любом конечном отрезке,и неограниченна в окрестности точки. Если существует предел, то он называется несобственным интегралом второго рода и обозначается.

Теор.(Критерий Коши сходимости несобственных интегралов) Пусть задан интегралс единственной особенностью в точке(неограниченна в точкеили). Для его сходимости необходимо и достаточно выполнения условия Коши:.

Док.Рассмотрим функциюТогда сходимость интегралаозначает существование конечного предела функциипри, а этот конечный предел, согласно Критерию Коши для функции, существует в том и только том случае, когдаудовлетворяет условию:. Но. Теорема доказана.

2. Несобственные интегралы. Их свойства

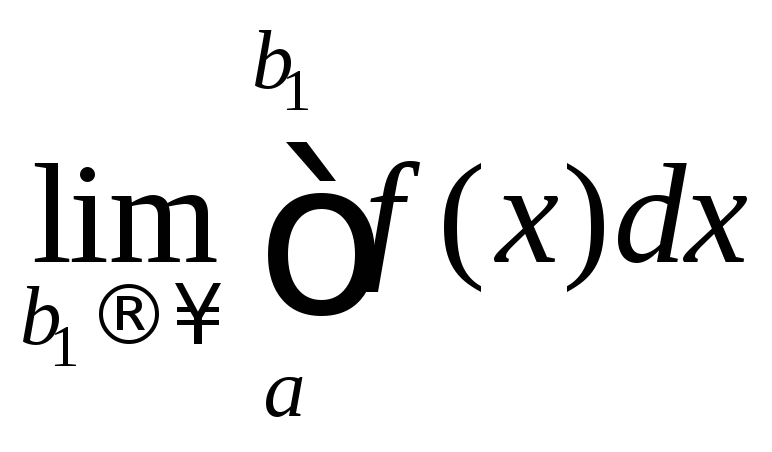Опр.Пустьзадана на лучеи интегрируема на любом конечном отрезке. Если существует предел, то он называется несобственным интегралом первого рода и обозначается.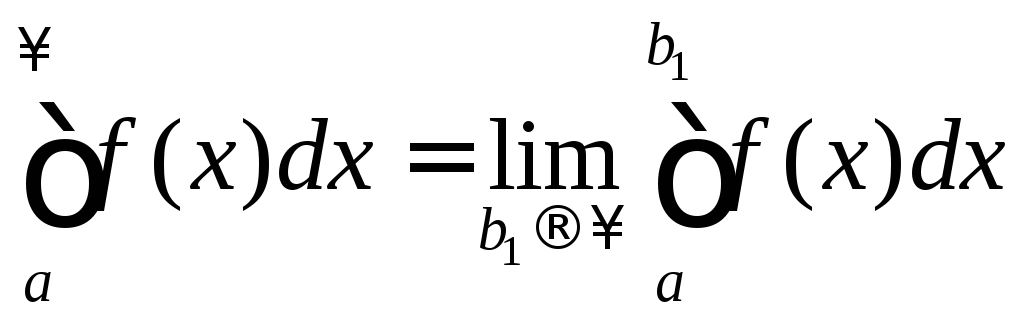

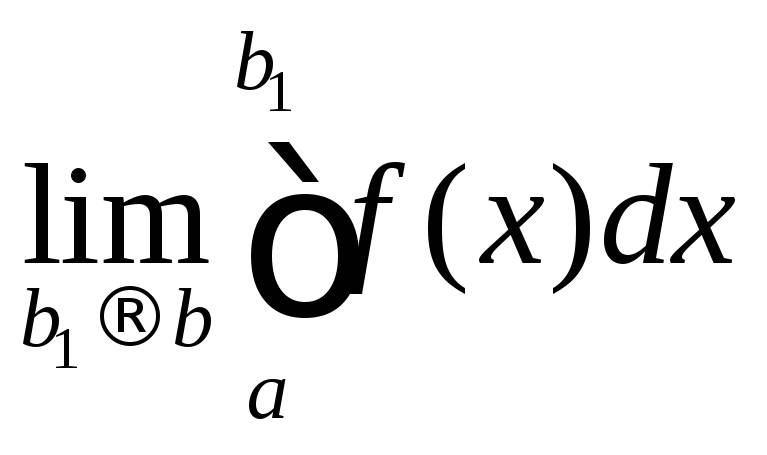Опр.Пустьзадана на полуинтервале, интегрируема на любом конечном отрезке,и неограниченна в окрестности точки. Если существует предел, то он называется несобственным интегралом второго рода и обозначается.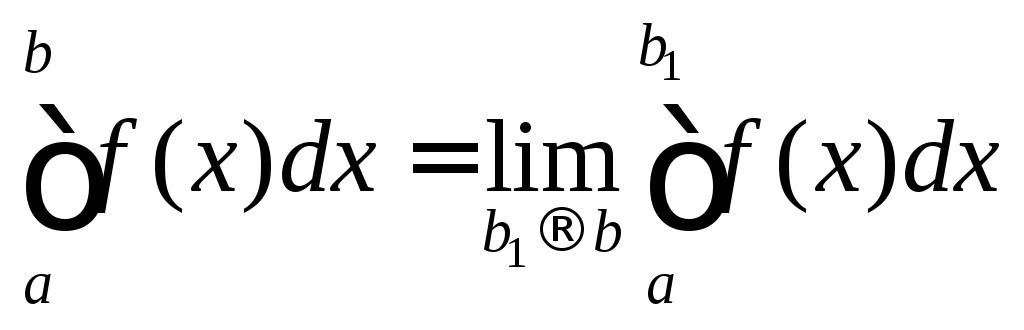

Свойства несобственных интегралов

1. и, особенность в точке- сходятся и расходятся одновременно. (Критерий Коши формулируется одинаково).

2. =+.

(Является следствием равенства =+).

3. Если - сходится, то сходится, причем.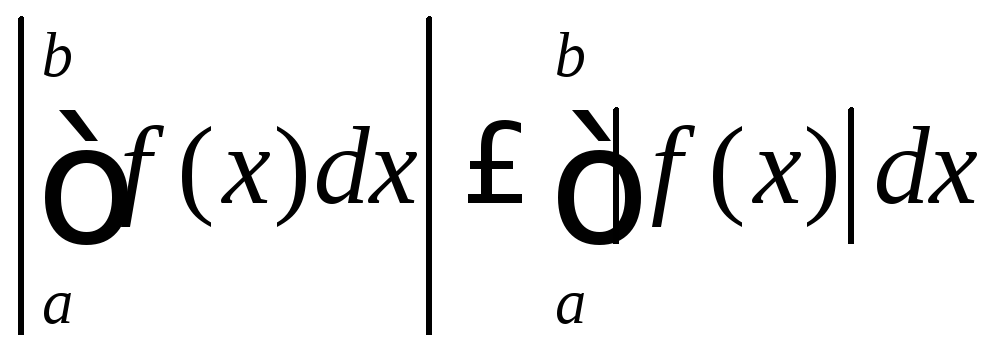

( Из условия Коши сходимости интеграла следует условие Коши для интеграла, т.к. справедливо неравенство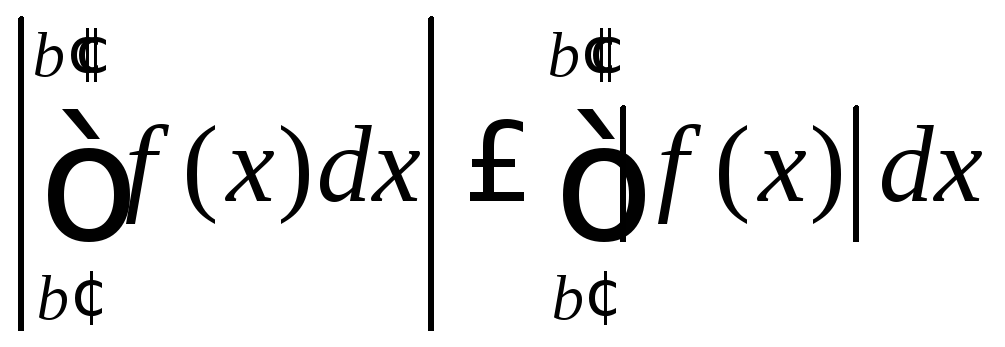. Воспользуемся неравенствомВ силу сходимости интегралов существуют пределы от левой и правой частей. Переходя к пределам, получаем неравенство.)

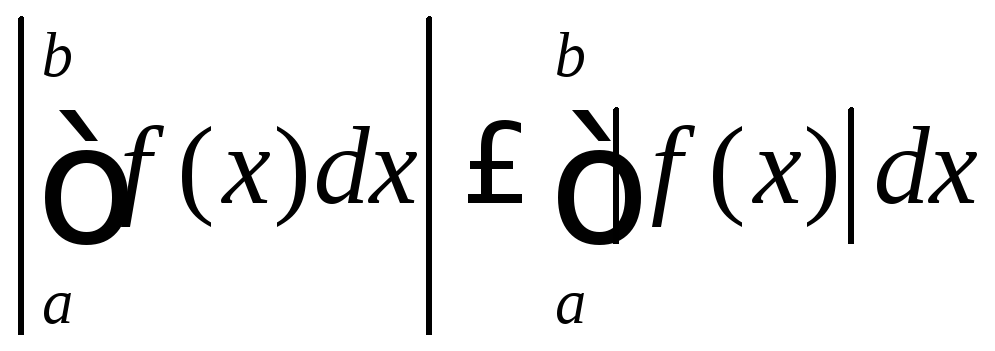3. Необходимое и достаточное условие сходимости несобственных интегралов от неотрицательных функций

Теор.Если, то для сходимостинеобходимо и достаточно, чтобы функциябала ограничена сверху, т.е..

Док.Так каквозрастающая функция, то из сходимости интеграла следуетОбратно, есливозрастающая функция и ограничена сверху, то она имеет конечный предел. Теорема доказана.

4. Признак сравнения

Теор.(Признак сравнения). Есливыполняется условие, тогда:

а). Из сходимости следует сходимость;

б). Из расходимости следует расходимость.

Док.а). ИмеемТак как, то по предыдущей теоремесходится.

б). Из расходимости следует расходимость. Предположим обратное, чтосходится, тогда по пункту а)тоже сходится. Противоречие. Теорема доказана.

5. Предельный признак сравнения

Теор.(Предельный признак сравнения). Пусть функциииположительны и, тогда несобственные интегралыисходятся и расходятся одновременно.

Док.. Раскрывая последнее неравенствои используя признак сравнения, получим, что интегралыисходятся и расходятся одновременно. Теорема доказана.

6. Открытые, замкнутые, ограниченные, связные множества

Пусть - некоторое множество точек в пространстве.

Опр.Точканазывается внутренней точкой, если существуетокрестность точки, содержащаяся в множестве.

Опр.Множество называется открытым, если все его точки внутренние.

Опр.Точканазывается граничной точкой множества, если в любойокрестности этой точки существуют точки, как принадлежащие множеству, так и не принадлежащие множеству.

Опр.Множество называется замкнутым, если ему принадлежат все граничные точки.

Опр.Множествоназывается ограниченным, если существуетмерный шар с центром в начале координат, такой, что.

Опр.Множество называется связным, если любые две его точки можно соединить непрерывной прямой, принадлежащей этому множеству.

Опр.Областью называется открытое связное множество.