Лекция №9

Тема: «Методы и модели нелинейного программирования для исследования операций СТС»

План:

1. Задачи и общие понятия нелинейного программирования. Почему нелинейное? Переход от линейного программирования к нелинейному. Точность линейного решения, решение первого приближения для нерешения.

2. Общая задача Н.П.

3. Геометрическая интерпретация задач Н. П.

4. Экономическая задача Н. П.

5. Четыре класса задач Н.П.

1.-2. Постановка задачи

В задаче нелинейного программирования требуется найти значение многомерной переменной х= (), минимизирующее целевую функцию f (x) при условиях, когда на переменную х наложены ограничения типа неравенств, i=1,2,…,m, а переменные, т.е. компоненты вектора х, неотрицательны:.

Иногда в формулировке задачи ограничения имеют противоположные знаки неравенств. Учитывая, однако, что если , то, всегда можно свести задачу к неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком равенства, например, то их можно представить в виде пары неравенств,, сохранив тем самым типовую формулировку задачи.

Метод неопределенных множителей Лагранжа

Условия экстремума функции, которые рассмотрены выше, позволяют найти, так называемый, безусловный экстремум. Однако, в большинстве практических задач принятия решения требуется принять решение - определить экстремум критерия оптимальности при условии, что на независимые переменные наложены ограничения, имеющие вид равенств. Типичными примерами подобных задач служат задачи, в которых требуется оптимальным образом распределить заданное количество ресурсов, чтобы принятая оценка эффективности процесса имела при этом максимальное или минимальное значение. Для решения таких задач в классическом анализе используется метод неопределенных множителей Лагранжа. Сами задачи получили название задач на условный экстремум.

Пусть требуется найти экстремум функции, например, минимум

Q (, при условии

,

Согласно методу Лагранжа для решения задач на условный экстремум функции составляется вспомогательная функция Лагранжа, которая определяется соотношением

,

где , = - неопределенные множители Лагранжа.

Таким образом, задача нахождения условного экстремума функции сводится к задаче нахождения безусловного экстремума функции, но число неизвестных в ней n + k (uι, ι = 1, n; λj, j = 1, k).

Как известно из п.1.2 необходимым условием безусловного экстремума функции является равенство нулю частных производных, которые для данного конкретного случая записываются в виде

.

и дает n уравнений для определения неизвестных. Эта система уравнений дополняется к уравнениям и, следовательно, получается (n + k) неизвестных и (n + k) уравнений.

Метод множителей Лагранжа дает лишь необходимые условия существования условного экстремума для непрерывных функций, имеющих также непрерывные производные, поэтому найденные значения переменных могут и не давать экстремума функции Q (u1,., un), их надо проверить с использованием достаточных условий экстремума функции многих переменных.

В окончательном решении задачи фактически множители Лагранжа не известны, поэтому задача совместного решения системы, иногда ставится как задача исключения "k" неизвестных переменных uι с последующим решением остающейся системы n уравнений с n неизвестными.

Задача Лагранжа имеет "n - k" степеней свободы.

2. Геометрическая интерпретация метода множителей Лагранжа

Интерес представляют геометрический смысл множителей Лагранжа. Для такой интерпретации лучше рассмотреть задачу с двумя неизвестными и одним ограничением.

Пусть требуется найти минимум функции при условии. Если минимум существует, то в пространстве функцияQ должна иметь вид воронки, а условие связи - это некоторая поверхность.

На рис.4, б изображены на плоскости переменных u1, u2 линии уровня функции Q (u1, u2) и ограничение φ (u1, u2) = 0, представляющее собой линию. Составляется вспомогательная функция Q (u1, u2) = Q (u1, u2) + λφ (u1, u2). Необходимое условие экстремума дает:

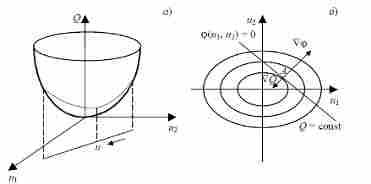
Рисунок 1.4 - Геометрический смысл множителей Лагранжа:

а - пространственное изображение;

б - изображение проекции на плоскость u2 - u1

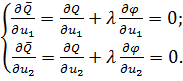
или

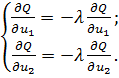
В точке А - точке касания линии с линией равного уровня функциииимеют общую касательную и необходимое условие минимума представляет собой условие пропорциональности двух векторов: вектора - градиента функции и вектора- градиента функции

Два вектора пропорциональны друг другу лишь в том случае, если они коллинеарные. Так как градиент функции перпендикулярен касательной к линии уровня, то в точке А выполняется условие, и множитель является коэффициентом пропорциональности между векторами и

Рассмотрим задачу нелинейного программирования, содержащую только две переменные, записанную в виде

,…………….

(x) <, x = ().

Как уже отмечалось, функция f (x) называется целевой функцией, а неравенства , i= 1,.,m называются ограничениями задачи. Множество точек, удовлетворяющих ограничениям задачи, называется допустимым множеством задачи.

Решить задачу нелинейного программирования графически - значит найти такую точку из допустимого множества, через которую проходит линия уровня f (,) = С, имеющая максимальное значение величины С из всех линий уровня, проходящих через допустимые точки задачи.

Как и в случае задач линейного программирования, для задач нелинейного программирования, содержащих только две переменные, возможна графическая интерпретация.

Наиболее существенное отличие задачи нелинейного программирования от линейных задач заключается в том, что оптимальное решение может находиться как на границе допустимого множества, так и являться его внутренней точкой.

Этапы графического решения задач нелинейного программирования можно сформулировать следующим образом.

Этап 1. На плоскости наносятся геометрические места точек, соответствующих каждому уравнению из ограничений задачи (x) =, i= 1,.,m. Строится допустимое множество задачи. Если допустимое множество задачи пусто, то задача не имеет решения.

Этап 2. Строятся линии уровня целевой функции f (,) = С при различных значениях параметра С.

Этап 3. Определяется направление возрастания (для задачи максимизации) или убывания (для задачи минимизации) линий уровня целевой функции.

Этап 4. Определяется точка допустимого множества, через которую проходит линия уровня с максимальным (для задачи максимизации) или минимальным (для задачи минимизации) значением параметра С. Если целевая функция не ограничена сверху (для задачи максимизации) или не ограничена снизу (для задачи минимизации) на допустимом множестве, то задача не имеет решения.

Этап 5. Для найденной точки определяют ее координаты = (,)и значение целевой функции в данной точке f= (,)

Решим следующую задачу нелинейного программирования, используя геометрическую интерпретацию

,

.

Построим линии, соответствующие ограничениям задачи и вычислим область определения функции (рис.3.1).

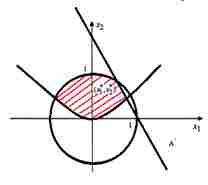
Рисунок 3.1 - Область определения функции

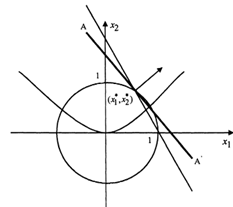
Рисунок 3.2 - Линия уровня функции

Линия уровня, соответствующая максимальному параметру С и проходящая через какую-либо точку допустимого множества, изображена на рисунке 3.2 АА’. Координаты оптимальной точки находятся из системы уравненийоткуда.