Лекция №10

Тема: «Численные методы поиска оптимального значения нелинейной целевой функции»

План:

1. Задачи численных методов в поиске оптимального значения целевой функции (скорость нахождения min Фопт).

2. Классификация методов, избыточность алгоритма поиска, точность.

3. Анализ и необходимость условия для использования конкретных чис. Методов.

4. Общие методы поиска «minФ»

5. Градиентные методы.

6. Специальные методы.

1. Все известные численные методы отыскания экстремума нелинейных функций в зависимости от используемой информации для получения следующей точки можно разделить на три основные группы.

Прямые методы, использующие только текущие значения оптимизируемой функции.

Методы первого порядка, использующие дополнительно  и значения первой производной функции.

Методы второго порядка, требующие знания и второй производной оптимизируемой функции.

Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом).^[2]

Методы оптимизации классифицируют в соответствии с задачами оптимизации:

• Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.

• Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.

Существующие в настоящее время методы поиска можно разбить на три большие группы:

1. детерминированные;

2. случайные (стохастические);

3. комбинированные.

По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.

По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:

• Задачи оптимизации, в которых целевая функция 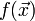 и ограничения  являются линейными функциями, разрешаются так называемыми методами линейного программирования.

• В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:

  • есл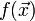и  и  — выпуклые функции, то такую задачу называют задачей выпуклого программирования;

  • если 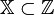, то имеют дело с задачей целочисленного (дискретного) программирования.

По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:

• прямые методы, требующие только вычислений целевой функции в точках приближений;

• методы первого порядка: требуют вычисления первых частных производных функции;

• методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.

Помимо того, оптимизационные методы делятся на следующие группы:

• аналитические методы (например, метод множителей Лагранжа и условия Каруша-Куна-Таккера);

• численные методы;

• графические методы.

В зависимости от природы множества X задачи математического программирования классифицируются как:

• задачи дискретного программирования (или комбинаторной оптимизации) — если X конечно или счётно;

• задачи целочисленного программирования — если X является подмножеством множества целых чисел;

• задачей нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерноговекторного пространства.

• Если же все ограничения и целевая функция содержат лишь линейные функции, то это — задача линейного программирования.

Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование.

Математическое программирование используется при решении оптимизационных задач исследования операций.

Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:

• Определение границ системы оптимизации

  • Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается

• Выбор управляемых переменных

  • «Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)

• Определение ограничений на управляемые переменные

  • … (равенства и/или неравенства)

• Выбор числового критерия оптимизации (например, показателя эффективности)

  • Создаём целевую функцию

Численные методы безусловной оптимизации нулевого порядка

Решение многих теоретических и практических задач сводится к отысканию экстремума (наибольшего или наименьшего значения) скалярной функции f(х) n-мерного векторного аргументах. В дальнейшем под x будем понимать вектор-столбец (точку в n-мерном пространстве):

Вектор-строка получается путем применения операции транспонирования:

.

Оптимизируемую функцию f(x) называют целевой функцией или критерием оптимальности.

В дальнейшем без ограничения общности будем говорить о поиске минимального значения функции f(x) записывать эту задачу следующим образом:

f(x ) --> min.

Вектор х*, определяющий минимум целевой функции, называют оптимальным.

Отметим, что задачу максимизации f(x) можно заменить эквивалентной ей задачей минимизации или наоборот. Рассмотрим это на примере функции одной переменной (Рис. 2.1). Если х* - точка минимума функции y = f(x), то для функции y =- f(x) она является точкой максимума, так как графики функций f(x) и - f(x), симметричны относительно оси абсцисс. Итак, минимум функции f(x) и максимум функции - f(x) достигаются при одном и том же значении переменной. Минимальное же значение функции f(x), равно максимальному значению функции - f(x), взятому с противоположным знаком, т.е. min f(x) =-max(f(x)).

Рассуждая аналогично, этот вывод нетрудно распространить на случай функции многих переменных. Если требуется заменить задачу минимизации функции f(x₁, …, x_n) задачей максимизации, то достаточно вместо отыскания минимума этой функции найти максимум функции f(x₁, …, x_n). Экстремальные значения этих функций достигаются при одних и тех же значениях переменных. Минимальное значение функции f(x₁, …, x_n) равно максимальному значению функции - f(x₁, …, x_n), взятому с обратным знаком, т.е. min f(x₁, …, x_n) =max f(x₁, …, x_n). Отмеченный факт позволяет в д Рис. 2.1. Экстремум

В реальных условиях на переменные x_j, i=1, …. n, и некоторые функции g_i (х), h_i(х), характеризующие качественные свойства объекта, системы, процесса, могут быть наложены ограничения (условия) вида:

g_i (х) = 0, i=1, …. n,

h_i (х) <= 0, i=1, …. n,

a <= x <= b,

где

 ; 

Такую задачу называют задачей условной оптимизации. При отсутствии ограничений имеет место задача безусловной оптимизации.

Каждая точка х в n-мерном пространстве переменных х₁, …, х_n, в которой выполняются ограничения, называется допустимой точкой задачи. Множество всех допустимых точек называют допустимой областью G. Решением задачи (оптимальной точкой)называют допустимую точку х*, в которой целевая функция f(х) достигает своего минимального значения.

Точка х* определяет глобальный минимум функции одной переменной f(x), заданной на числовой прямой Х , если x ^* X иf(x^*) < f(x) для всех x^*  X (Рис. 2.2, а). Точка х* называется точкой строгого глобального минимума, если это неравенство выполняется как строгое. Если же в выражении f(х*) <= f(x) равенство возможно при х, не равных  х*, то реализуетсянестрогий минимум, а под решением в этом случае понимают множество х* = [x^*  X: f(x) = f(x^*)] (Рис. 2.2, б).

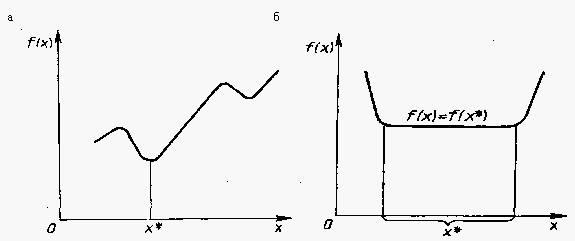
В дальнейшем говорить только о задаче минимизации.

Рис. 2.2. Глобальный минимум. а - строгий, б - нестрогий

Точка х*  Х определяет локальный минимум функции f(x) на множестве Х , если при некотором достаточно малом e > 0 для всех х, не равных  х*, x  X, удовлетворяющих условию ¦х - х*¦<= e, выполняется неравенство f(х*) < f(х). Если неравенство строгое, то х* является точкой строгого локального минимума. Все определения для максимума функции получаются заменой знаков предыдущих неравенств на обратные. На Рис. 2.3 показаны экстремумы функции одной переменной f(х) на отрезке [a, b] . Здесь х₁, х₃, х₆ - точки локального максимума, а х₂, х₄ - локального минимума. В точке х₆реализуется глобальный максимум, а в точке х₂ - глобальный минимум.

Рис. 2.3. Экстремумы функции