Математические методы / Лекции / Лекция №12

Лекция №12 Тема «Специальные численные методы для определения экстремального значения целевой функции»

План

1. Особенности целевых функций и необходимость разработки специальных численных методов.

2. Численный метод параллельных касательных (метод Пауэлла).

3. Метод «Штрафных функций».

4. Метод «Тяжелого шарика».

5. Метод «Золотого сечения».

1. Особенности целевых функций и необходимость разработки специальных численных методов.

В широком смысле целевая функция есть математическое выражение некоторого критерия качества одного объекта (решения, процесса и т.д.) в сравнении с другим. Примером критерия в теории статистических решений является среднеквадратический критерий точности аппроксимации. Цель – найти такие оценки, при которых целевая функция достигает минимума.

Важно, что критерий всегда привносится извне, и только после этого ищется правило решения, минимизирующее или максимизирующее целевую функцию.

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ^*, который доставляет минимальное значение f(χ^*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:

Допустимое множество — множество ;

Целевую функцию — отображение ;

Критерий поиска (max или min).

Тогда решить задачу  означает одно из:

Показать, что .

Показать, что целевая функция  не ограничена снизу.

Найти .

Если , то найти .

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек  таких, что всюду в некоторой их окрестности  для минимума и  для максимума.

Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

2. Метод параллельных касательных (метод Пауэлла) Этот метод использует свойство квадратичной функции, заключающееся в том, что любая прямая, которая проходит через точку минимума функции х*, пересекает под равными углами касательные к поверхностям равного уровня функции в точках пересечения (Рис. 2.7). Этот метод использует свойство квадратичной функции, заключающееся в том, что любая прямая, которая проходит через точку минимума функции х*, пересекает под равными углами касательные к поверхностям равного уровня функции в точках пересечения (Рис. 2.7). 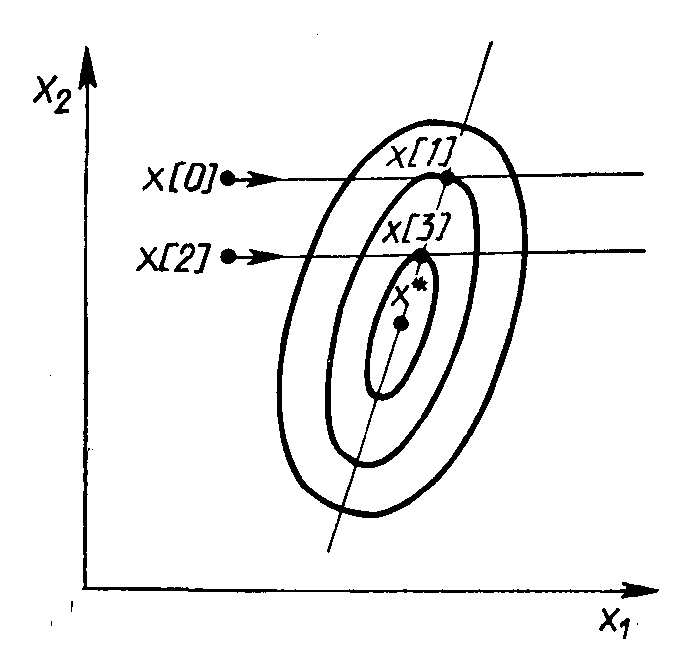Рис. 2.7. Геометрическая интерпретация метода Пауэлла Суть метода такова. Выбирается некоторая начальная точка х[0] и выполняется одномерный поиск вдоль произвольного направления, приводящий в точку х[1] . Затем выбирается точка х[2], не лежащая на прямой х[0] - х[1], и осуществляется одномерный поиск вдоль прямой, параллельной х[0] - х[1],. Полученная в результате точка х[3] вместе с точкой х[1] определяет направление x[1] - х[3] одномерного поиска, дающее точку минимума х^*. В случае квадратичной функции n переменных оптимальное значение находится за п итераций. Поиск минимума при этом в конечном счете осуществляется во взаимно сопряженных направлениях. В случае неквадратичной целевой функции направления поиска оказываются сопряженными относительно матрицы Гессе. Алгоритм метода параллельных касательных состоит в следующем. 1. Задаются начальной точкой x[0]. За начальные направления поиска р[1], ..., р[0] принимают направления осей координат, т. е. р [i] = е[i], i = 1, ..., n (здесь e[i]= (0, ..., 0, 1, 0, … 0)^T). 2. Выполняют n одномерных поисков вдоль ортогональных направлений р[i] , i = 1, ..., п. При этом каждый следующий поиск производится из точки минимума, полученной на предыдущем шаге. Величина шага а_k находится из условия f(x[k] + а_kр[k]) = f(x[k] + ар[k]). Полученный шаг определяет точку х[k+1] = х[k] + а_kр[k] . 3. Выбирают новое направление p =-x[n] - х[0] и заменяют направления р[1], ..., р[n] на р[2], ..., р [n], р. Последним присваивают обозначения р[1], ..., р[n] 4. Осуществляют одномерный поиск вдоль направления р = р[n] = х[n] - х[0]. Заменяют х[0] на х[n+1] = х[n] + а_nр[п] и принимают эту точку за начальную точку х[0] для следующей итерации. Переходят к п. 1. Таким образом, в результате выполнения рассмотренной процедуры осуществляется поочередная замена принятых вначале направлений поиска. В итоге после n шагов они окажутся взаимно сопряженными.

3. Метод штрафных функций

Изложение метода

Основная задача метода штрафных функций состоит в преобразовании задачи минимизации функции

с соответствующими ограничениями, наложенными на х, в задачу поиска минимума без ограничений функции

Функция  является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию Z, т.е. увеличивала её значение.В этом случае минимум функции Z будет находиться внутри области ограничений. Функция , удовлетворяющая этому условию, может быть не единственной. Задачу минимизации можно сформулировать следующим образом:

минимизировать функцию 

при ограничениях .

Функцию  удобно записать следующим образом:

где r – положительная величина.

Тогда функция  принимает вид

.

Если х принимает допустимые значения, т.е. значения, для которых , то Z принимает значения, которые больше соответствующих значений  (истинной целевой функции данной задачи), и разность можно уменьшить за счет того, что r может быть очень малой величиной. Но если х принимает значения, которые хотя и являются допустимыми, но близки к границе области ограничений, и по крайней мере одна из функций  близка к нулю, тогда значения функции , и следовательно значения функции Z станут очень велики. Таким образом, влияние функции  состоит в создании «гребня с крутыми краями» вдоль каждой границы области ограничений. Следовательно, если поиск начнется из допустимой точки и осуществляется поиск минимума функции  без ограничений, то минимум, конечно, будет достигаться внутри допустимой области для задачи с ограничениями. Полагая r достаточно малой величиной, для того чтобы влияние  было малым в точке минимума, мы можем сделать точку минимума функции без ограничений совпадающей с точкой минимума задачи с ограничениями.

Алгоритм метода штрафных функций

Пусть имеется следующая задача: Минимизировать  при ограничениях ,.

Начальный этап Выбрать  в качестве константы остановки, начальную допустимую точку ∈, для которой , , скаляр  и . Положить k=1 и перейти к основному этапу.

Основной этап. k-я итерация.

Первый шаг. При исходной точке  решить следующую задачу безусловной оптимизации:

 минимизировать, где

 - параметр, значения которого убывают с каждой итерации  при ;  - положительные весовые коэффициенты.

Примерами штрафных функций являются:

1) обратная функция 

2) логарифмическая функция 

Положить  равным оптимальному решению задачи минимизации и перейти ко второму шагу.

Минимизация штрафной функцию может быть выполнена любым методом безусловной оптимизации, например, градиентным.

Второй шаг

Если , то остановиться. Решение является искомым.

В противном случае положить . Изменить  и перейти к первому шагу (k+1)-й итерации.

4. Метод тяжелого шарика

Метод базируется на аналогии с движением тяжелого материального шарика по наклонной поверхности. Скорость шарика при движении вниз будет возрастать, и он будет стремиться занять нижнее положение, т.е. точку минимума.

X_i+1 = X_i - (X_i –X_i-1) – h gradF(X_i)

При  = 0 – метод превращается в обычный градиентный. При 0 <  < 1 можно получать различную эффективность метода, которая будет зависеть и от h. Вдали от оптимума поиск будет ускоряться, а вблизи возможны колебания около минимума.

 - определяет память алгоритма, т.е учитывает влияние предыдущей точки, поэтому увеличение этого параметра вблизи минимума может привести к более быстрому затуханию, если градиент функции мал. Предпочтителен, когда глобальный минимум ярко выражен.

5.Метод золотого сечения — метод поиска значений действительно-значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации

Пусть задана функция . Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки  и  такие, что:

Иллюстрация выбора промежуточных точек метода золотого сечения.

, где  — пропорция золотого сечения.

Таким образом:

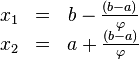
То есть точка  делит отрезок  в отношении золотого сечения. Аналогично  делит отрезок  в той же пропорции. Это свойство и используется для построения итеративного процесса.

Алгоритм 

1) На первой итерации заданный отрезок делится двумя симметричными относительно его центра точками и рассчитываются значения в этих точках.

2) После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поискаминимума), отбрасывают.

3) На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку.

4) Процедура продолжается до тех пор, пока не будет достигнута заданная точность.

Формализация 

Шаг 1. Задаются начальные границы отрезка  и точность .

Шаг 2. Рассчитывают начальные точки деления:  и значения в них целевой функции: .

Если  (для поиска max изменить неравенство на ), то 

Иначе .

Шаг 3.

Если , то  и останов.

Иначе возврат к шагу 2.