Kursovik_Terver_25

Задача 1.При перевозке 100+α=125деталей, из которых 1+α=26 были забракованы, утеряна 1 стандартная деталь. Найти вероятность того, что наудачу извлеченная деталь (из оставшихся) окажется стандартной.

n1 =125 − общее количество деталей

n2 = n1 -1 = 124 - общее количество деталей после потери одной стандартной детали

m1 = n1 - 26 = 99 - количество стандратных деталей

m2 = m1 -1 = 98 - количество стандартных деталей после потери одной стандартной детали

А- событие {наудачу извлеченная деталь (из оставшихся) окажется стандартной}

Найти : P( А)

Решение

После того, как одна стандартная деталь была утеряна, осталось 124детали, из которых 98 стандартных. Вероятность появления из этой совокупности стандартной детали найдем по классической формуле теории вероятностей:

P( A) = m2 = 98 = 49 n2 124 62

Ответ : P( A) = 49 62

Задача 2. На один ряд, состоящий из 4+α=29мест, случайно садятся 4+α=29учеников. Найти вероятность того, что 3 определенных ученика окажутся рядом.

a = 29 − количество мест

b = 29 − количество учеников

А− событие {три определенных ученика окажутся рядом}

Найти : P( А)

Решение

Случайный эксперимент – рассаживание 29 учеников в один ряд. Элементарный

конкретных ученика (например, те, которые имеют номера 1,2 и 3) окажутся рядом. Мысленно объединим 3-х учеников в одного, тогда общее количество учеников

урны во вторую перекладывают один шар. Какова вероятность после этого вынуть: а) белый шар из I урны

б) белый шар из II урны.

a1 = 30 − количество белых шаров в 1 − ой урне b1 = 35 − количество черных шаров в 1 − ой урне a2 =15 − количество белых шаров во 2 − ой урне b2 = 32 − количество черных шаров во 2 − ой урне А− событие {из 1 − ой урны извлекли белый шар}

B − событие {из 2 − ой урны извлекли белый шар}

Найти : а)P( А), б)P(B)

Решение

а) Рассмотрим следующие возможные гипотезы:

H1 - гипотеза {из 1- ой урны во 2 - ую переложили белый шар}

H2 - гипотеза {из 1- ой урны во 2 - ую переложили черный шар}

Т.к. в первой урне всего 30+35=65 шаров, из которых 30 белых и 35 черных шаров, то вероятности гипотез равны:

При выполнении гипотезыН1 в первой урне останется29 белых и 35 черных шаров,

при выполнении гипотезыН2 – 30 белых и 34 черных шаров, поэтому условные вероятности наступления событияА при выполнении этих гипотез равны:

Применим формулу полной вероятности:

При выполнении гипотезы Н1 во второй урне станет 16 белых и 32 черных шаров,

при выполнении гипотезы Н2 – 15 белых и 33 черных шара, поэтому условные вероятности наступления события B при выполнении гипотез равны:

По формуле полной вероятности имеем:

Ответ: P(A) = 6 , P(B) = 201 13 624

Задача 5.На I складе имеется 10+α=35изделий, из которых 3 бракованных; на II складе находятся 15+α=40 изделий, из которых 5 бракованных. Из каждого склада выбирается по одному изделию случайным образом. После чего из этой пары отбирается одно изделие, которое оказалось небракованным. Какова вероятность, что это изделие из I склада?

n1 = 35 − общее количество изделий на 1 складе

a1 = 3 − количество бракованных изделий на 1 складе b1 = 32 − количество стандартных изделий на 1 складе n2 = 40 − общее количество изделий на 2 складе

a2 = 5 − количество бракованных изделий на 2 складе b2 = 35 − количество стандартных изделий на 2 складе

А− событие {из пары изделий извлечено стандартное изделие}

Найти : P(Н1 A)

Решение

Рассмотрим следующие возможные гипотезы:

H1 - гипотеза {из пары изделий отобрано изделие с 1- го склада}

H2 - гипотеза {из пары изделий отобрано изделие со 2 - го склада}

Вероятности этих гипотез:

F(х) = F(2) = P(X < 2) = 100 / 126 + 25 / 126 = 125 / 126 ;

4) если х > 2 , то X может принять любое значение 0; 1; 2 поэтому

F (х) = P( X < x) = 100 / 126 + 25 / 126 +1 / 126 = 1 .

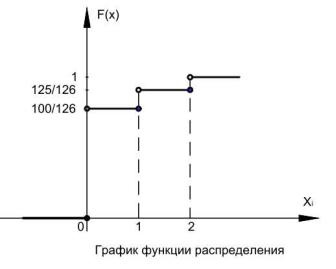
Построим график функции распределения F (x)

Задача 7.Даны независимые случайные величины X и Y заданы своими рядами распределений:

Составить закон распределения их суммы - случайной величины Z=X+Y и проверить выполнение свойства математического ожидания:

М(X+Y)=M(X) + M(Y)

Решение

Найдем возможные значения zij = xi + y j

z1 = 2 -1 =1 z2 = 2 + 0 = 2

z3 = 2 + 26 = 28 z4 = 4 -1 = 3 z5 = 4 + 0 = 4

z6 = 4 + 26 = 30

Находим вероятности этих значений:

p1 = P(Z =1) = P(X = 2)× P(Y = -1) = 0,7 ×0, 4 = 0, 28 p2 = P(Z = 2) = P(X = 2)× P(Y = 0) = 0,7 ×0,1 = 0,07 p3 = P(Z = 28) = P(X = 2)× P(Y = 26)= 0,7 ×0,5 = 0,35 p4 = P(Z = 3) = P(X = 4)× P(Y = -1)= 0,3×0, 4 = 0,12 p5 = P(Z = 4) = P(X = 4)× P(Y = 0) = 0,3×0,1 = 0,03 p6 = P(Z = 30) = P(X = 4)× P(Y = 26)= 0,3×0,5 = 0,15

Упорядочив значенияZв порядке возрастания,получим закон распределения:

Проверим выполнение свойства математического ожидания

n

M ( X ) = ∑xi × pi = 2 × 0, 7 + 4 × 0, 3 = 2, 6

i =1

t

M (Y ) = ∑y j × p j = -1× 0, 4 + 0 × 0,1 + 26 × 0, 5 = 12, 6

j =1

Для нахождения дисперсии случайной величины Х воспользуемся формулой

Задача 9.Производится телефонный опрос потребителей некоторой продукции. Каждый потребитель независимо от других может дать положительный отзыв о продукции с вероятностью α / 40 = 25 / 40 = 0, 625 . Составить закон распределения случайной величины Х - числа положительных отзывов среди 3-х опрошенных потребителей. Найти математическое ожидание и дисперсию числа положительных отзывов среди 3-х опрошенных.

p = 0, 625

X − случайная величина числа положительных отзывов среди

3 − х опрошенных потребителей

Найти : закон распределения случайной величины X , M ( X ), D( X )

Решение

Случайная величина Xраспределена по биномиальному закону распределения. В

данной задаче она может принимать значения 0, 1, 2, 3. Соответствующие

вероятности, будут определяться по формуле: