ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ 2

1 Общая теория уравнивания по методу наименьших квадратов 4

2 МАТРИЧНАЯ ФОРМА ПОЛУЧЕНИЯ УРАВНЕНИЙ ПОПРАВОК 6

3 МАТРИЧНАЯ ФОРМА ПОЛУЧЕНИЯ НОРМАЛЬНЫХ УРАВНЕНИЙ 8

4 РЕШЕНИЕ ЗАДАЧИ УРАВНИВАНИЯ ПРИ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЯХ 9

5 ИЗМЕРЯЕМЫЕ ФУНКЦИИ В ТРИАНГУЛЯЦИИ ВТОРОГО КЛАССА 11

6 ФОРМУЛЫ ДЛЯ КОЭФФИЦИЕНТОВ УРАВНЕНИЙ ПОПРАВОК 12

7 ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ СВОБОДНЫХ ЧЛЕНОВ УРАВНЕНИЙ ПОПРАВОК 14

8 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ТРЕУГОЛЬНИКОВ 15

9 ВЫЧИСЛЕНИЕ ПРИБЛИЖЕННЫХ КООРДИНАТ 17

10 ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ УРАВНЕНИЙ ПОПРАВОК 17

11 СОСТАВЛЕНИЕ УРАВНЕНИЙ ПОПРАВОК 18

ВВЕДЕНИЕ

Общая теория уравнивания по методу наименьших квадратов параметрическим способом хорошо дается в [1], а и матричной форме – в [3,4,5]. Параметрический способ под старым названием «Посредственные, или косвенные, измерения» также представлен в классической литературе [9] и отличается простым и очень понятным изложением и пояснениями. Теория уравнивания триангуляции параметрическим способом дается в [2] и [7]. Практические указания и подробное описание всех действий при составлении уравнений поправок в ходе уравнивания триангуляции даны в [8]. В настоящем учебном пособии излагается одновременно и общая теория уравнивания, как в обычной, гак и в матричной форме, и теория уравнивания триангуляции параметрическим способом, а также приводится подробное описание практических действий при уравнивании конкретной сети триангуляции. В таком виде пособие в максимальной степени соответствует лабораторным занятиям по уравниванию триангуляции студентов четвертого курса астрономо-геодезической специальности физического факультета Уральского государственного университета.

Результаты измерений в астрономии и геодезии можно рассматривать как один из объектов изучения методами математической статистики. В математической статистике имеют дело с большой совокупностью предметов, которая называется генеральной совокупностью. Из генеральной совокупности наудачу выбирают определенное количество предметов, которое называют случайной выборкой из генеральной совокупности. В применении к астрономии и геодезии генеральной совокупностью следует считать весь обычно бесконечный набор возможных результатов наблюдений, а случайной выборкой - ряд значений полученных результатов. Число результатов наблюдений называется объемом выборки.

Пусть произведено n наблюдений, результаты которых образуют случайную выборку {q₁, q₂, ..., q_n}. Поскольку астрономические и геодезические измерения протекают в условиях быстро меняющейся метеорологической обстановки, изменяющегося состояния приборов и самого наблюдателя, каждое из множества {q_i, i = 1, 2, ..., n} наблюдений, строго говоря, нельзя считать элементом выборки из одной и той же генеральной совокупности. Другими словами, каждый результат наблюдений q_i следует считать значением случайной величины, распределенной по иному закону, чем остальные в данной выборке. Но обычно считается, что при получении данного ряда наблюдений условия наблюдений менялись незначительно и поэтому результаты наблюдении соответствуют одной и той же генеральной совокупности.

В еще большей мере вышеприведенное замечание относится к рядам наблюдений, произведенных в разные дни, разными наблюдателями и разными приборами. Но и в этих случаях, часто считают, что эти наблюдения имеют один и тот же закон распределения вероятностей.

Хотя мы исходим из того, что читатель знаком с основными понятиями теории вероятностей и математической статистики, напомним, что среднее из всех значений случайной величины, составляющих генеральную совокупность, называется математическим ожиданием этой случайной величины. Для непрерывной случайной величины оно равно

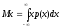
где Мх - математическое ожидание случайной величины х, р(х) – плотность вероятности случайной величины x, определяемая формулой

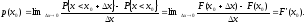
Функция F(x₀)=P{x<x₀} называется функцией распределения вероятности.

В настоящем пособии мы считаем, что математическое ожилание результатов измерений совпадает с истинным значением измеряемой величины, т.е. если истинное значение измеряемой величины x*, то

Mx= x*

Мы называем в этом случае ошибки измерений случайными.Если обозначить случайную ошибку i-го измерения через _i, то

MΔ_i=0

Если M_i = c 0, то это означает, что ошибки _i содержат в себе систематическую ошибку, равную с.

Задачей измерений является определение истинного значения измеряемой величины. Если бы была известна вся генеральная совокупность результатов измерений, то дело свелось бы к простому вычислению среднего арифметического, а в случае непрерывной случайной величины - к вычислению интеграла (1). Но в результате измерений получается только случайная выборка из генеральной совокупности, и необходимо по случайной выборке определять истинное значение измеряемой величины, т. е. математическое ожидание случайной величины, представляющей собой все возможные результаты измерений. Вычисленное значение математического ожидания по случайной выборке называется его оценкой. Формула, по которой производится это вычисление, тоже называется оценкой является среднее арифметическое из результатов измерений, если измерения равноточные. (Если измерения неравноточные, то - среднее весовое.)

Математическая обработка астрономо-геодезических измерений производится по методу наименьших квадратов. Целью такой обработки является получение оценок нужных нам величин, оценка точности полученных оценок и точности функций оцениваемых величин.

Конкретной задачей настоящего пособия является теоретическое обоснование и подробное описание составления уравнений поправок при уравнивании триангуляции второго класса параметрическим способом. (Параметрический способ уравнивания - это уравнивание по методу наименьших квадратов, когда ищется решение, удовлетворяющие не условному, а прямому минимуму функции Ф=[р²], где _i(i=1,2,…,n) – поправки в результаты наблюдений, р_i(i=1,2,…,n) - веса наблюдений, а квадратные скобки - гауссово обозначение суммы:

[pv²]=p₁v₁+p₂v₂+…+p_nv_n

Триангуляция второго класса в системе построения государственной геодезической сети представляет собой так называемую заполняющую сеть внутри полигонов первого класса астрономо-геодезической сети. В натуре это совокупность точек, координаты которых должны быть получены из триангуляционных работ. Сеть точек связана направлениями, представляющими собой сеть треугольников, углы в которых должны быть измерены. Точность измерения углов на пунктах сети второго класса не должна быть меньше 1,00", вычисленной по невязкам треугольников. Длины сторон треугольников колеблются от 7 до 20 км. Базисные стороны, т.е. стороны триангуляции, длины которых должны быть известны или из непосредственных измерении или по вычислениям базисной сети, располагаются равномерно и не реже, чем через 25 треугольников, при этом одна базисная сторона должна быть расположена примерно в середине полигона.

Относительная ошибка базисных сторон должна быть не более 1:300000. В сети второго класса пункты Лапласа определяют на концах базисной стороны или стороны полигонометрического хода, находящейся в середине полигона. Пункты Лапласа - это пункты триангуляции, на которых производятся астрометрические определения широты, долготы и азимута. Точность их определения 0,30" для астрономической широты, 0,03 секунды времени для астрономической долготы и 0,50" для астрономического азимута.

Согласно государственному стандарту [6] сеть триангуляции второго класса подлежит уравниванию, т.е. математической обработке по методу наименьших квадратов. Важнейшей частью такой обработки является составление уравнений поправок.