Н.Б. Лесных
Математическая обработка геодезических измерений. Метод наименьших квадратов. Практикум
Содержание
1. Действия с матрицами
1.1. Общие сведения
1.2. Сложение матриц
1.3. Умножение матриц
1.4. Транспонирование матриц
1.5. Обратная матрица
1.6. Запись систем линейных уравнений в матричном виде
1.7. Дифференцирование матричных выражений
2. Коррелатный способ уравнивания
2.1. Условные уравнения
2.2. Весовая функция
2.3. Нормальные уравнения коррелат
2.4. Составление нормальных уравнений коррелат
2.5. Решение нормальных уравнений по алгоритму Гаусса
2.6. Оценка точности по материалам уравнивания
2.7. Блок-схема коррелатного способа уравнивания
2.8. Уравнивание нивелирной сети коррелатным способом
2.9. Уравнивание геодезического четырехугольника коррелатным способом
3. Параметрический способ уравнивания
3.1. Параметрические уравнения
3.2. Нормальные уравнения
3.3. Составление нормальных уравнений
3.4. Весовая функция
3.5. Решение нормальных уравнений способом обращения
3.6. Оценка точности по материалам уравнивания
3.7. Блок-схема параметрического способа уравнивания
3.8. Уравнивание нивелирной сети параметрическим способом
3.9. Уравнивание углов на станции параметрическим способом
Список литературы
1. Действия с матрицами
Общие сведения
Таблица чисел, содержащая m строки n столбцов, называется матрицей размера m · n
Числа aij - элементы матрицы; i - номер строки (i = 1, 2, ..., m); j - номер столбца (j = 1, 2, ..., n).
Если m ≠ n - матрица прямоугольная.
Матрица, в которой число строк равно числу столбцов (m = n), называется квадратной.
Матрица размера 1 · n - вектор-строка; размера m · 1 - вектор-столбец.
Матрица, все элементы которой равны нулю (aij = 0), называется нулевой.
Элементы aii квадратной матрицы образуют ее главную диагональ. Если aij = aji (i ≠ j), квадратная матрица симметрична.
Если в квадратной матрице aij = 0 (i ≠ j), матрица называется диагональной.
Диагональная матрица с элементами aii = 1 называется единичной:
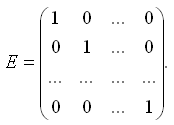
Следом квадратной матрицы называется сумма ее диагональных элементов:
Сложение матриц
Матрицы одинакового размера можно складывать.
Сmn = Аmn + Вmn ; сij = аij + вij.
Свойства суммы: А + В = В + А;
А + В + С = (А + В) + С = А + (В + С).
Задание № 1. Найдите алгебраическую сумму матриц:
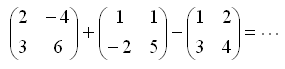
Умножение матриц
Матрицы можно умножить, если число столбцов первой матрицы равно числу строк второй.
Cmk = Аmn · Bnk; cij = ai1 · b1j + ai2 · b2j +...+ ain · bnj; (i = 1, 2, ..., m), (j = 1, 2, ..., k).
Пример. С23 = А22 В23 = ?
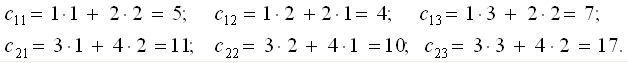
Свойства произведения:
А · В· С = (А · В) · С = А · (В · С);
А · В · В · А;
А(В + С) = АВ + АС - умножение слева;
(В + С)А = ВА + СА - умножение справа;
0А = А0 = 0; ЕА = АЕ = А;
Задание № 2. Выполните умножение матриц, укажите размер результата.
1.
2.
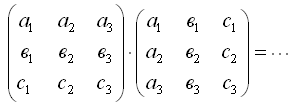
Обозначить: а1а1 + а2а2 + а3а3 = [аа], а1в1 + а2в2 + а3в3 = [ав] и т.д.
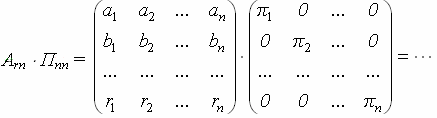
3.
Транспонирование матриц
Если в матрице Аmn поменять местами строки и столбцы, получим транспонированную матрицу Anmт.
Пример.
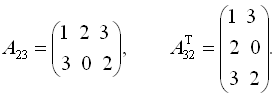
Свойства транспонирования:
(Ат)т = А; (А + В)т = Ат + Вт; (А В С)т = СтВтАт - транспонированное произведение матриц равно произведению транспонированных матриц, записанных в обратной последовательности. Если А = Ат, матрица симметрична.
1.5. Обратная матрица
Квадратная матрица называется неособенной, если ее определитель не равен нулю. Всякая неособенная матрица имеет обратную. Это такая матрица А-1, которая, будучи умножена на исходную А слева или справа, дает единичную
А-1А = АА-1 = Е.
Свойства обратной матрицы:
(А-1)-1 = А; (А В С)-1 = С-1В-1А-1 - обратная матрица произведения равна произведению обратных матриц, взятых в обратной последовательности;
(А-1)т = (Ат)-1.
Пример. (А В С)-1 (СтВтАт)т = С-1В-1А-1А В С = С-1В-1ЕВС = С-1ЕС = Е.
Задание № 3. Выполните преобразования матричных выражений.
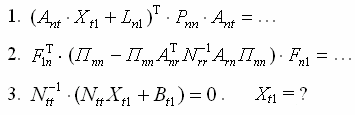
1.6. Запись систем линейных уравнений в матричном виде
-
система линейных уравнений.
Обозначим:
-
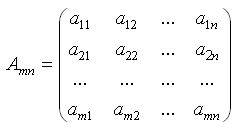матрица коэффициентов,
-
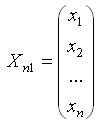вектор неизвестных,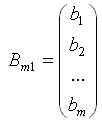
- вектор свободных членов.
AmnXn1 + Bm1 = 0 - матричная запись системы уравнений.
Задание № 4. Запишите системы линейных уравнений в матричном виде.
