Билеты по матану

Билет№1 матрицы,основные определения

Опр1. Прямоугольной матрицей А размера m x n называется произвольная система элементов({а}) совместимости k=m*n расположенная в виде таблицы, содержащей «m» строк и «n» столбцов

Опр 2.квадратной матрицей А порядка «n»называется матрица размера n х n ( число строк= число столбцов)

Опр 3. Верхняя треугольная матрица- матрица вида

К_mn-трапецевидная матрица

Опр 4. Матрица А_1n- называется матрицей строкой.опр 5. Матрица А_1m-называется матрицей столбцом. опр 6. Транспонированной матрицей называется матрица А^t_nm, которая получена из основной матрицы А_mn путем замены;строк на стоблцы

Билет № 2 действия над матрицами

Матрицы Аmn и Вmn называются равными если порядки матриц A и B одинаковы и aij=bij (i=1,2,...,m; j=1,2,...,n)

Опр1. Суммой двух матриц одинакового размера Аmn и Вmn называется матрица того же размера Cmn= Amk+Bmn, cij = aij + bij

Опр 2. Произведением матрицы Аmn на число альфа называется матрица Cmn того же размера,для которого cij = aij * альфа.

Опр 3. Разность двух матриц одинакового размера определяется равенством. А-В=A+(-1)B,тоесть C=A-B

Свойства операций сложения и умножения на число:

A+B=B+A -- свойство коммутативности;

A+(B+C)=(A+B)+C -- свойство ассоциативности;

A+0=A ;наличие нейтрального элемента

A+(-A)=0 наличие противоположного элемента

альфа(A+B)={ alpha}A+{\alpha} -- свойство дистрибутивности;

({\alpha}+{\beta})A={\alpha}A+{\beta}A ;

{\alpha}*({\beta}*A)=( {\alpha} *{\beta})*A ;

1* A=A

Умножение матрицы на матрицу

Опр. Amp x Bpn называется матрица С размера mn (строка х столбец). Змечание. Операция умножения применима только тогда,когда число строк матрицы В=числу строк матрицы А.

А*В=В*А-перестановочные матрицы

Свойства операции умножения:

A(BC)=(AB)C-ассоциативность

A(B+C)=AB+AC, (A+B)C=AC+BC –дистрибутивность

Аmn*En=Em*Amn-наличие единичного элемента

Билет №3Определитель.вычисление.

К каждой квадратной матрицы поставим соответствующие чило,которое будет учитывать все ее элементы,это число назовем определителем и назовем detA

Вычисление определителей. Опр 1. Порядком определиеля det квадратной матрицы,для которой считается этот определитель 1) detA₁=/а₁₁/=а11 определитель первого порядка 2) detA2=

a11 a12

a21 a22= a11a22 − a12 a21 3) detA3- определитель матрицы,где 3 строки и 3 столбца

Билет №4 теорема разложения

Дополнительным методом Mij квадратной матрицы Аn назвается определитель матрицы n−1–го порядка, полученной из исходной вычеркиванием i–ой строки и j–го столбца, на пересечении которых стоит данный элемент. Опр. Определитель матрицы n-го порядка det элемента, detАn=Д=∑aijAij

Билет №5 свойства определителей

Опр. Транспонированным определителем det определитель транспонированной матрицы.величина транспонированного определителя совпадает с величиной исходного определителя . Методом матричной индукции можно распростронить это свойство на определители любого порядка. Следствий1. Строки и столбцы определителя равноправны. Свойство 1. Определитель меняет знак при перестроении двух его строк(столбцов).

Следствие 2.определитель с 2мя одинаковыми строками(столбцами) равен 0. Свойство 2. Если все элементы строки(столбцы) определителя содержат обычный множитель, то его можно вынести за знак определителя.следствие 3.определитель с 2мя пропорциональными строками(столбцами) равен 0. Свойство 3. Если все элементы строки(столбца) являются суммами из одинакового числа слагаемых,то определитель равен сумме определителей, в которых элементами строки служат отдельные слагаемые. Следствие 4. Определитель не изменяется если по всем элементам какой-либо строки(столбца) прибавить элементы 2строки,уможение на оно и то же число. Свойство 4. Если все элемены какой-либо строки матрицы раввен 0, то определитель этой матрицы равен 0.

Билет №6 обращение матриц

Опр. Обратной матрицей к данной квадратной матрице Аndet квадратная матрица ,если

An*A^-1n= A^-1n*An=En

Опр. Квадратная матрица называется вырожденной,если ее определитель равен 0 и не вырожденной если detА не равен 0.

Теорема об обратной матрице. Для существования обратной матрицы необходимо и достаточно,чтобы detА не равен 0,т.е матрица была невырожденной,при этом ,где А^с={Аij}

Свойства обращения матриц:

1. Если матрицу дважды обратить,получится матрица

2. 

3. 

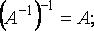
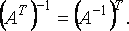
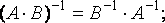
Билет №7 элементарные преобразования матриц

1. Перестановка 2х строк

2. умножение строки или столбца матрицы на ненулевое число

3. прибавление к некоторой строке матрицы другой ее строки, предварительно умноженной на произвольный коэффициент

4. транспонирование матриц

опр. Эквивалентными называются матрицы, полученные одна из другой с помощью конечного числа элементарных преобразований.

Билет №7 ранг матрицы

Опр1. Минором К-го порядка матрицы Amn det определитель,составленный из элементов этой матрицы, находящихся на пересечении строк с номерами i1,i2…ik и столбцов j1, j2…jk ,причем 1<i1<i2…<ik<m, 1<j1<j2<…<jk<n

Опр 2. Рангом матрицы A det число r(A) ,если:

1)у матрицы А существует ненулевой минор порядка r(A). 2)любой минор матрицы А,иммеющий порядок r(A)+1 и выше равен 0

Рангом нулевой матрицы назовем число 0. Вычисление ранга матрицы методом элементарных преобразований.

Билет №9 вычисление ранга матрицы методом элементарного преобразования

Теорема 1. Ранги эквивалентных матриц одинаковы. Можно показать,что посредством серии элементарных преобразований любая матрица Amn может быть приведена к трапецивидной Мmn. Ранг трапецевидной матрицы равен числу ее ненулевых строк,т.е тех строк, в которых есть хотя бы одно нулевое число.

Билет №10 СЛУ,основные определения

Решением слу называется любая совокупность чисел,которая будучи подставленной в уравнении системы,обращает их в тождестве.

Билет № 11 классификация слу

Опр. Совместной называется СЛУ,если она имеет хотя бы одно решение:система не имеющая решения называется несовметной. Опр. Определенной называется система,если она имеет ровно одно решение и неопределенной если имеет более одного решения.

Билет№12 исследование слу

1)теорема Кронекера–Капелли1(условия несовместимости). Для того что бы СЛУ1 была совершена,необходима и достаточно, чтобы ранг основной матрицы системы.r(A)=r(A^p)

2) теорема Кронекера–Капелли2(условие определенности). Совместное СЛУ является определенной, если r(A)= числу неизвестных r(A)=n

Зам.если r(A)не равен «n» следует r(A)<n и система содержит r(A)независимых уравнений остальные явления их линейной комбинацией и их можно отбросить .зам. если число уравнений совпадает числу неизвестных,т.е матрица- квадрат, условием определенности является невырождена этой матрицы.

Билет №13 матричный метод решения определенной СЛУ

Т.к слу определена => detA не равно 0=>r(A)=n => существует обратная матрица Помножив матричное уравнение на матрицу слева

Зам.этот метод очень трудоемкий,однако он станоится эффективным в случае если надо решить несколько систем, с одинаковыми явными частями и различными столбцами свободных челенов.

Билет №14 метод крамера

Опр.1. главным определителем системы называется определитель основной матрицы сиситемы A=detA. Опр.2определители называются XK det определитель,полученный из главного заменой К-го столбца столбцом свободных челенов.

Теорема крамера. Если главный определитель системы , то система имеет единственное решение, определяемое по формуле . Зам. Этот метод эффективно применяется в случае если число уравнений не превосходит 3.

Билет №17 однордные слу

Опр1. Однородные слу det система у которой все свободные челены=0. Опр2.Правильным det решение системы,состоит из одних 0.

Теорема1. Для того что бы однородное слу число нетривиальное решение,необходимо и дастаточно,что бы ранг очновной матрицы системы был меньше числа неизвестных. Теорема 2. Для того что бы однородное слу число неизвестных n, который = числу уравнений m,имело нетривиальное решение,необходимо и достаточно что бы det=0,матрица ….

Билет №18 Линейный пространства, основные определения

Множество L называется линейным или векторным пространством, если:

1.Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y

1. x + y = y + x − сложение коммутативно;

2. x + (y + z) = (x + y) + z − сложение ассоциативно;

3. x + 0 = x − существует единственный нулевой элемент 0 ( x + 0 = x для любого x из L);

4. x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x ( x + (−x) = 0 для любого x из L).

2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x, причём:

1. α·(β·x) = (α·β)·x − умножнение на число ассоциативно: ;

2. 1·x = x − для любого элемента x из L.

3. Операции сложения и умножения на число связаны соотношениями:

4. α·(x + y) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;

5. (α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.

Элементы линейного пространства называются векторасм и обозначаются мал.лат.буквами a,b,c,d… числа β,альфа,гамма.

Билет №19 линейное преобразование векторов

V³ x1={x11,x12,x13}, x2{x21,x22,x23}

X1+x2={x11+-x21, x12+-x22, x13+-x23}

Альфа(α)*x1={ α*x11, α*x12, α*x13}

По аналогии можно определить операцию сложения,выч., и умножения на число в линейном пространстве любой природы

Билет №20 скалярное произведение векторов

Опр1. Скалярным произведением двух элементов линейного пространства называется отображение элемента на число удовлетворяющий следующим оксиомам.

1. Коммуникативность (z1,z2)=(z2,z1)

2. Однородность (z1, альфа Z2)= альфа(z1,z2)

3. Ассоцитивность (z1,z2+z3)=(z1,z2)+(z1,z3)

4. Неотрицательностьь скалярного квадрата(z1,z1)>=0 и (z1,z1)=0<=> z1=0

Опр2. Нормой вектора линейного пространства с веденным в нем скалярным произведением называется отображение вектра на число удоалетворяющего следующим ее 3ем оксиомам

1. ||Z1||>=0, ||Z1||=0 =>0- неотрицательность

2. Абсолютная однородность ||альфа*Z1||=|альфа |*||Z1||

3. ||Z1+z2||=<||z1||+||z2||- неравенство треугольника

Теорема4. В линейном пространстве с введенным в нем сколярным произведением норма вектора равно норме квадратному из скалярного квадрата||Z1||=кореньZ1*Z1 =кореньZ1²

Билет №21условия параллельности и перпендикулярности векторов

Z1=(z11,z12…,Z1n), z2=(z21,z22…,z2n)

Z1||z2z11/z21=z12/z22=….z1n/z2n

Z1перпендикулярно z2(z1,z2)=0 (z11*z21+z21*z22….+z1n*z2n=0)

Билет№22 векторное произведение векторов

Опр3.векторным произведением z1 z2в пространстве R³ взятых в даной последоватеьности называется вектор Z3 в пространстве R³

Z3=[z1,z2]=z1*z2и удовлетворяет следующим аксиомам

1. При перестоновки 2х множителей знак меняется. Антикоммутативность [z1,z2]=-[z2,z1]

2. Дистрабутивность- [z1,z2+z3]=[z1,z2]+[z1,z3]

3. Ассоциативность умноженное на число[z1, альфа z2]=альфа [z1,z2]

4. [I,j]=k

Свойство векторного произведдения

1)векторное произведние двух векторов равно нулевому вектору

2) векторное произведение 2х коллиниальных векторов равна нулевом вектору

3) векторное произведение оригинально каждому из своих

4) норма векторного произведения численно равна площади параллелограмма построенного на этих векторах S=||[a,b]||

Билет №23 смешанное произведение векторов

Если 2 вектора умножить векторно,а затм полученный вектор умножить на 3й,то получится смешанное произведение. Опр1. Смешанным произведением трех векторов х1,х2,х3 взятых в данной последоватльности называются (z1,z2,z3),удовлетворяющим следующим аксиомам.

1)антикоммутативность (z1,z2,z3)=-(z1,z2,z3)

2)диструбутивность[z1,z2+z3,z4)=(z1,z2,z4]+[z1,z3,z4)

3)ассоциативность относительно умножения на число

Свойства смешанного произведения

1)смешанноые произведения компланарных векторов равно нулю.зам.копланарные-вектора лежащие на одной плоскости.

2)если среди векторов со множиетлями имеются положиетльные вектора

Теорема. смешенные произведения векторов заданные координатами в базе ijk равно определителю каждая строка которого составлена из координат соотетствующего сомножителя.

(Хз надо или нет)Абсолютная велечина смешенного произведения трех вектооров а,в,с численно равна модулю объема параллелепипеда построенного на векторах сомножителя

Билет №54 схема исследования функции

1)найти ООФ

2)исследовать поведение функции в окрестностях точек разрыва

3)исследовать на четность и нечетноть

4)точки с пересечениями с осями координат. OY;x=0=>y0=f(0). OX:y=o=>x1,x2-корни f(x)=0

5)асимптоты а)верникальная б)наклонная (у=кх+в) в)горизонтальная (если к=0)

6)исследование фукнкии на монотонность экстремума

7)исследование на выпуклость/вогнутость и перегиб

8) построить график функции

Билет №53 асимтоты функции

Опр1.асимптотой кривой у= f(x) имеющие бесконечную ветвь называется прямая L, ткая что расстояние от точки функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Асимптоты;вертикальная(х=х0), наклонная(у=кх+в),горизтнальная( у=в,т.к к=0 )

Теорема 1.для того что бы пямая у=кх+в была наклонной асимптотой кривой у= f(x) необходимо и достаточно чтобы к= (написать в одну формулу+-бескон),

Билет№36 теорема о б/м

Теорема 1. , -б/м при хx0

1)+- б/м при xx0 2)* б/м при хx0

Теорема2.произведение ограниченной функуии на бесконечно малую есть б/м функуия.если f(x)ограниченная функция. - б/м при хx0 => f(x)*0

Теорема 3. Пусть f(x) определена в U(x0) тогда (вместо бескон, написать а) f(x)-а-б/м при хx0

Теоема 4.

Билет №37теоремы о пределах

Теорема1. Если у функции существует предел,то этот предел единственныйй.

Теорема2. Предел алгеброический суммы конечного числа функции равен алгеброической суммы их пределов при условии того что последнее существует и конечное

Теорема3. Предел произведения конечного числа функции равен произведению пределов со множителями,если эти пределы существуют и конечны. Следствие.при нахождении предела произведения постоянный множитель можно вынести за знак предела .lim[k*f(x)]=k*lim*f(x),k-const.

Теорема4.предел частного двух функций имеющий конечный предел равен частному пределов при условии того что предел знаменателя не равен 0.

Теорема 5.limf(x)=a, limg(x)=b,=>lim [f(x)]=a (везде лим стремиться к х0)

Теорема 6. Если в окрестности точки альфа выполняется условие и при этом функции и стремятся к одному и тому же пределу А , то и функция также стремится к тому же пределу, т.е.

Теорема 7. Если фукнция f(x) не отрицательна в некоторой окрестности х0 и существует limf(x)=a,то а больше либо равно 0.

Теорема 8. Если limf(x)=a, limg(x)=b тогда, 1)f(x)=g(X), для каждого x пренодлежит U(x0)=>a=b. 2)f(x)=<g(x)для каждого x пренодлежит U(x0)=>a=<d

Билет №38сравнение б/м

Альфа(х),бэта (х)-б/м при х->х0

Опр1.если limальфа(х)/бэта(х) не существует,то альфа и бэта-несравнимые б/м

Опр 2. если ,то то альфа и бэта-б/м одного порядка малости при х->х0

Опр3. Если (вместо 0-1),то альфа и бэта-эквивадентными б/м при х->х0

Опр4. Если то - б.м.более низшего порядка малости чем .

Опр5. Если то - б.м. более высокоо порядка малости чем .

Опр6.если ,то -б/м, к-го порядка малости относительно

Билет№39 теория об эквивалентных б/м

Теорема1. Предел отношений б/м не измениться если любую из них заменить на эквивалентную.

Теорема2.сумма ограниченного числа б/м,разных порядков эквивалентно тому слогаемому порядок которого ниже.

Билет №40 непрерывность функции

Опр1.функцияf(x) -непрерывна в точне х0,если:1)U(x0)-определена в некоторой окрестности точки х0 2)существует limf(x) 3)limf(x)=f(x0) (все стремиться к х0)

Опр2. Функция называется непрерывной в области если она непрерына в каждой точне этой области.

Опр3. Функция называется непрерывной в точке х пренадлеж.(а,в),если бесконечно малому прирощению аргумента в Δх,соответствует б/м Δу

limΔy=0(стремиться Δх к 0)

билет №42 Дифференциальное исчисление функции 1 переменной. основные определения

опр1. Приращение функции у=f(x) в точке х=х0 называется Δf(x0)=f(x0+Δx)-f(x0)

опр2. Производной функции у=f(x) называется предел отношений прирощения функции к прирощению аргумента при стремлении последнего к нулю произвольным образом Δx->Δf/Δx

зам.1) для того что бы функция была дифференцируема-необходимо,чтобы она была непрерывна в этой точке 2)производная функции в точке может быть =+-∞

Билет №51 монотонность функции

Опр1. Функция называется возрастающей на промежутке [а,в] для любого x1<x2 €[a,b]=>f(x1)≤f(x2) [f(x1)≥f(x2)]

Опр2. Промежутки возраст. И убывающ. Функции называются промежутки монотонностями

Теорема1.(достаточное условие моното.)для того что бы дифференцируемая функция f(x) была монотонно убыв(возр) на промежутке [а,в] достаточно что бы f’(x)>[f’(x)<0]

Опр3. Точка х0 называетс я точной локального max(min) для функуии у=f(x) если сущ. Хотя бы одна окрестность этой точки U(xo):x€U(x0)=>f(x0)>f(x)[f(x0)<f(x)]

Опр4. Точной локального экстремума называется точкой локатьного max(min). Теорема 2.необходимое условие экстремума. Если фукнуия f(x) имеет в точке х0 производную и достигает в ней локального экстремума,то f’(x0)=0

Опр5. В точке в котторой первая производная =0,называется критическими точками первого рода или неопределенными. Теорема3.(достаточное условие экстремума) Если непрерывная

функция у = f(x) дифференцируема в некоторой б-окрестности критической точки х0 и при переходе через нее (слева направо) производная f’(х) .меяется знак с плюса на минус, то Х0 есть точка максимума;с минуса на плюс, то ха - точка минимума.

теорема 4 Если в точке хо первая производная функции f(x)равна нулю и f'(хо) = О). а вторая производная в точке хо существуети отлична от нуля (f’’(xo) не равно О). то при f”(xo) < О В точке хо функция имеет максимум и минимум - при f”(xo) > О.