Лекции по Матанализу ч2

Добавил:

neus500 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский авиационный институт (национальный исследовательский университет)

Предмет:

Высшая математика

Файл:

Замечание. Необходимым и достаточным условием существования производной

функции f x

в точке x является равенство односторонних производных, т.е.

.pdf

Скачиваний:

147

Добавлен:

24.07.2017

Размер:

1.2 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

К У Р С

МАТЕМАТИЧЕСКОГО АНАЛИЗА

Часть 2

2011

Оглавление
Оглавление.......................................................................................................................................................................	2
Дифференциальное исчисление функции одной переменной ................................................................................	3
Производная функции, ее геометрический и физический смысл.........................................................................	3
Односторонние производные функции в точке......................................................................................................	5
Основные правила дифференцирования...................................................................................................................	6
Дифференциал функции. ..........................................................................................................................................	11
Теоремы о среднем. ....................................................................................................................................................	12
Производные и дифференциалы высших порядков. .............................................................................................	15
Формула Тейлора. ......................................................................................................................................................	15
Представление некоторых элементарных функций...........................................................................................	18
по формуле Тейлора...................................................................................................................................................	18
Раскрытие неопределенностей. Правило Лопиталя. .........................................................................................	22
Исследование функций с помощью производной. .................................................................................................	24
Возрастание и убывание функций. Точки экстремума..................................................................................	24
Исследование функции на экстремум с помощью производных высших порядков. ..............................	27
Выпуклость и вогнутость кривой. Точки перегиба. ......................................................................................	27
Схема исследования функций ............................................................................................................................	28
Уравнения некоторых типов кривых в параметрической .................................................................................	34
форме. ..........................................................................................................................................................................	34
Окружность. ...........................................................................................................................................................	34
Эллипс. ....................................................................................................................................................................	34
Циклоида. ...............................................................................................................................................................	35
Астроида. ................................................................................................................................................................	35
Производная функции, заданной параметрически. .............................................................................................	36
Исследование функций, заданных параметрически. ...........................................................................................	36

Дифференциальное исчисление функции одной переменной

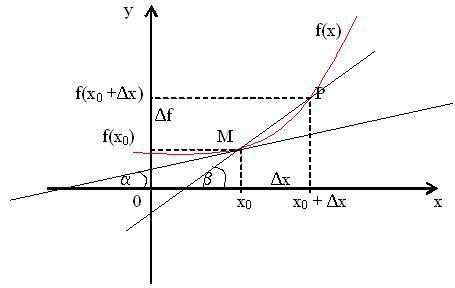
Производная функции, ее геометрический и физический смысл.

Определение. Производной функции f x в точке x x0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

	f (x) lim	f (x x) f (x)
	f (x) lim	x
	x 0	x

Пусть f x определена на некотором промежутке	a,b . Тогда	tg	f	тангенс
			x

угла наклона секущей МР к графику функции.

lim tg lim		f	f (x0 ) tg ,
x 0	x 0	x		f x в точке x0 , f x0 .
где - угол наклона касательной к графику функции
Угол между кривыми может быть определен как угол между касательными,
проведенными к этим кривым в какойлибо точке.
Уравнение касательной к кривой:	y y0		f (x0 )(x x0 )
Доказательство. Известно, что уравнение прямой имеет вид
		y kx b .
Но так как эта прямая является касательной к графику функции					y f x	в точке
x0 , f x0 , то ее угловой коэффициент	k	должен быть равен f x0 . Чтобы найти b ,
воспользуемся тем, что касательная проходит через точку x0 , f x0 . Значит
b f x0 kx0 f x0 f x0 x0
Подставляя в уравнение прямой	y kx b найденные значения				k и b ,	получим
уравнение касательной к графику функции		f x в точке x0 , f x0 :
y y0 f (x0 )(x x0 )
Уравнение нормали к кривой: y y0			1	(x x0 ) .

			f (x0 )

Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

Физический смысл производной.

Пусть функция f t - закон движения (изменения координат) материальной точки, t

– время. Тогда

f t lim	f	- мгновенная скорость движения материальной точки в момент
t 0	t
времени t

Соответственно, вторая производная функции – скорость изменения скорости, т.е. ускорение.

Производные основных элементарных функций.

1) С 0,

C const ;

cos x

9) sin x

2) x

;

10)

cos x sin x

11)

tgx

cos 2 x

12)

ctgx

x 2

sin 2 x

5) e

13)

arcsin x

1 x2

6) a

ln a

14)

arccos x

1 x2

7) ln x

15)

arctgx

1 x2

log a

16)

arcctgx

x ln a

Пример. Найти угловые коэффициенты касательных к параболе y 2x2

точках, абсциссы которых соответственно равны x1 1,

x2 2 .

Решение. Вычислим производные функции

f x

в точках x1 1,

x2 2 .

Так как

y 4x , то y 1 4, y 2 8. Значит, искомые угловые коэффициенты соответствующих

касательных будут равны

k 1 4, k 2 8.

Пример. Написать уравнение касательных к параболе

y x2 1

в точках

1, 2

0, 1 .

Решение. Находим угловые коэффициенты касательных в соответствующих точках

k1 y 1 2, k2 y 0 0 .

Тогда имеем

уравнения

касательных

y 2 2 x 1

y 1 0 .

Определение. Функция

y f x

называется дифференцируемой в точке x ,

если

приращение y функции

f x

в точке

x x0 , отвечающее приращению аргумента

x ,

может быть представлено в виде

f x0 A x x x

x - бесконечно

где A - постоянное число

(для точки

x x0 ),

не зависящее от

x ;

малая функция x , т.е. lim

x 0

› 0

f x0

f x0 A x o x

Иначе говоря, приращение

имеет вид

Далее покажем дифференцируемость некоторых функций.

1. y x2 2 .

Решение. y x x 2 2 x2

2 2x x x 2 ,

A 2x, x x .

2. y ln x .

Решение. y ln x x ln x ln 1

o x , A

3. y sin x
Решение.
y sin x x sin x 2 sin	x cos x	x	2 x		o x cos x	x

	2	2		2		2

o x

cos x cos

cos x

sin

x o x cos x 2 sin

cos x x o x

cos x x 2o x sin x

sin

f x

Теорема. Для того чтобы функция

была дифференцируемой в точке

x x0 ,

необходимо и достаточно чтобы f x имела в этой точке производную.

Доказательство.

y f x в т. x

1. Необходимость. Пусть

дифференцируема, тогда

y f x0 A x o x

Разделим y на

x и вычислим предел частного

y при х 0:

o x

lim

A .

x 0

С другой стороны

lim

f x0 . Значит,

f x0 существует и равна А.

x 0

y f x

2. Достаточность. Пусть функция

имеет производную, т.е.

lim

f x0 ,

x 0

Тогда разность функции

и предела

f x0 есть величина бесконечно малая при

x 0 ,

т.е. y f x0 x ;

x 0

при x 0 ,

Следовательно y f x0 f x0 x x x .

Положим f x0 A

для точки

x x0 , тогда y f x0 A x x x .

Теорема доказана.

y f x

Теорема. Дифференцируемая в точке

x x0

функция

непрерывна в этой

точке.

y f x0 A x x x

Доказательство.

Так

как

условие

дифференцируемости,

то

при

x 0

получаем

y 0 . Последнее

означает

непрерывность функции

f x

в точке

x x0 .

y f x имеет в точке

Замечание. Дифференцируемая в точке

x x0

функция

(х0; f(x0)) касательную прямую.

Односторонние производные функции в точке.

Определение. Правой (левой) производной функции

f x в точке

x x0 называется

правое (левое) значение предела отношения

при условии, что это отношение существует.

) lim

)

lim

x 0

x 0 x

Если функция f x имеет производную в некоторой точке x x0 , то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во-первых функция может иметь разрыв в точке x0 , а во-вторых, даже если функция непрерывна в точке x0 , она может быть в ней не дифференцируема.

Пример: f x x - имеет в точке x 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.

В этом случае левая и правая касательные совпадают.

Основные правила дифференцирования.

Cy ,

C const

1) Cy

Доказательство. Рассмотрим функцию u x Cy x . Так как приращение функции u

имеет вид

u Cy x x Cy x C y ,

то

C y

и после перехода к пределу при x 0 ,

получим u c Cy x .

Обозначим далее u f x , v g x - функции, дифференцируемые в точке х.

2) u v

u v

Доказательство. Для суммы w u v имеем w u v , тогда

и после перехода к пределу при x 0 , получим

u v u v .

Аналогично доказывается утверждение для разности функций.

3) uv u v uv

Доказательство. Обозначим w uv . Тогда

w u x x v x x u x v x u x x v x u x x v x

u x x v x x v x v x u x x u x u x x v v x v

Откуда

w u x x v

v x u

и после перехода к пределу при x 0 получим

u v uv .

w uv

u v v u

, если v 0

Доказательство. Приращение функции w x

u(x)

равно

v(x)

u x x

u x

u x x v x v x x u x

v x x

v x

v x x v x


u x x v x u x v x u x v x v x x u x		v x u x x u x u x v x x v x
	v x x v x	v x x v x
	v x x v x	v x x v x
v x u v x u
v x x v x
v x x v x

Тогда после деления последнего равенства на

и перехода в нем к пределу при

x 0 , получим

u x

u (x)v(x) u(x)v (x)

v x

v2 (x)

Производная сложной функции.

Теорема.

Пусть

y f x ; u g y ,

причем область значений функции y входит в

область определения функции u .

Тогда

u x g (u) f x

Доказательство.

lim

x 0

y 0

x 0

( с учетом того, что если x 0 , то y 0 ,

т.к. y f x – непрерывная функция)

Тогда u x g (u) f x .

Теорема доказана.

Пример.

Найти производную функции y x cos x sin x

cos 2

x .

Сначала преобразуем данную функцию: y 12 sin 2x 12 cos 2 x

sin 2x

x2 cos 2x

2 cos x( sin x)

sin 2x x cos 2x sin x cos x x cos 2x.

Пример.

Найти производную функции y

x2 e x2

x2 1

(2xe x2 x

2 2xe x2 )(x 2 1) (2x)x 2 e x2

2x3e x2 2x5 e x2 2xe x2 2x3e x2

2x3e x2

(x2 1)2

(x 2 1)2

2xe x2 (x 4 1 x 2 )

2 1)2

Пример. Найти производную функции y ln tg

sin x

sin x x cos x

2 x

sin 2 x

cos

2sin

cos

sin x sin x x cos x

x cos x

sin 2 x

Пример. Найти производную функции y arctg

2x4

1 x8

8x3 (1 x8 ) ( 8x7 )2x4

(1 x8 )2 (8x3 8x11 16x11)

4x8

(1 x8 )2

(1 x8 )2 (1 x8 )2

(1 x

)

8x3 8x11

8x3 (1 x8 )

8x3

(1 x8 )2

1 x8

Пример. Найти производную функции y x2 ex2 ln x

y x2 e x

ln x x2 e x

2xe x

x2 e x

2x ln x xe x

2xe x

(1 x2 ) ln x xe x

xe x2 (1 2 ln x 2x2 ln x)

Логарифмическое дифференцирование.

Рассмотрим функцию y ln

ln x, при

x 0

ln( x), при

x 0

( x)

Тогда (ln x )=

, т.к. ln x

; (ln( x))


				f (x)
Учитывая полученный результат, можно записать ln			f (x)		.
Учитывая полученный результат, можно записать ln			f (x)	f (x)
	f (x)			f (x)
Отношение	f (x)	называется логарифмической производной функции f(x).
Отношение	f (x)	называется логарифмической производной функции f(x).
	f (x)

Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле

f (x) (ln f (x) ) f (x)

Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных или дробно-рациональных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.

Определение. Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет

показательно – степенной.
Пусть u f x и v g	x – функции, имеющие производные в точке x ,							f x 0 .
Найдем производную функции y uv . Логарифмируя, получим:
			ln y v ln u
		y	v ln u v				u
			v ln u v
		y					u
				v	u
	y u			v		v ln u
	y u			v		v ln u
					u


uv vuv 1u u v v ln u
Пример. Найти производную функции	f (x) (x2 3x) x cos x .
По полученной выше формуле получаем: u x2 3x;		v x cos x;
Производные этих функций: u 2x 3;	v cos x x sin x;

Окончательно:

f (x) x cos x (x2 3x) x cos x 1 (2x 3) (x2 3x) x cos x (cos x x sin x) ln(x2 3x)

Производная обратной функции.

Пусть требуется найти производную функции y f x при условии, что обратная ей

функция x f 1 y g y имеет производную, отличную от нуля в соответствующей точке. Для решения этой задачи воспользуемся равенством

y 1x x

Переходя к пределу при y 0 . Так как обратная функция дифференцируема, то изy 0 следует, что x 0 . Следовательно,

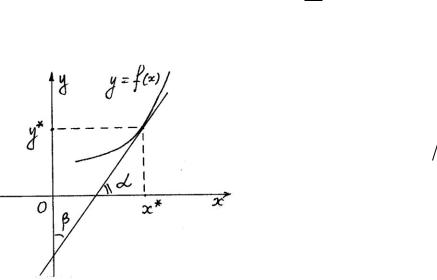
y 1

x xy

т.е. производная обратной функции обратна по величине производной данной функции. Выясним геометрический смысл производной обратной функции.

Так как			tg		f x0 , имеем
	x y	1		1		1
	x y			tg		tg 2

		yx
1		tg

	ctg
	ctg

Пример. Найти формулу для производной функции arctg x .

Функция

arctg x

является функцией,

обратной к функции tg x , т.е.

ее производная

может быть найдена следующим образом:

tgx;

x arctgy;

Известно, что y

(tgx)

cos 2 x ;

По приведенной выше формуле получаем:

d (arctgy)

d (arctgy) / dx

;

1/ cos 2 x

Т.к.

1 tg 2 x 1 y 2 ;

то

можно

записать

окончательную

формулу для

cos 2

производной арктангенса:

(arctgy)

y 2 ;

Таким образом, получены все формулы для производных арксинуса, арккосинуса и других обратных функций, приведенных в таблице производных.

Производная функции, заданной параметрически.

Если функция y f x задана параметрически, т.е.

x (t)

t ,

y (t)

(здесь функции

полагаем

дифференцируемыми), то ее производную

вычисляем по определению производной:

lim

(если он существует).

Т.к.

x t t 2 t t тогда

y t t 1 t t,

lim

t t 1 t t

t 0

t t 1 t t

t 0

Итак

(t)

при

x t .

(t)

Производная функции, заданной неявно

Пусть значения двух переменных x и y связаны между собой уравнением вида

F x, y 0 .
Пример: x2 y2 1 0 , x2	ln y 0 .
Определение. Если функция y f x , определенная на некотором интервале		a, b
такова, что уравнение F x, y 0	при подстановке в него y f x обращается в тождество

относительно x , то функция y f x называется неявно заданной уравнением F x, y 0 .

Определение.

Если

существует

предел

lim

F (x x, y) F (x, y)

то

он

называется частной производной по переменному х

функции

z F x, y

в точке

x, y

обозначается символами

или F x, y .

Определение. Если существует предел

lim

F (x, y y) F (x, y)

то он называется

y 0

частной производной

по

переменному у

функции

z F x, y

точке

x, y

обозначается символами

или F x, y .

Пусть имеем функцию двух переменных

z F x, y , где y f x

дифференцируемая

функция. Тогда F x, y

является функцией

переменного

как

сложная

функция

z F x, f x

Если переменная

получает приращение

x , то переменная

y f x также

принимает приращение y

в силу непрерывности

f x .

Откуда получим:

F F x x, y y F x, y F x x, y y F x, y y F x, y y F x, yFx x, y y Fy x, y

Тогда после деления равенства на x и перехода к пределу при x 0 получим:

lim

x F (x, y y)

lim

y F (x, y)

x 0

lim

F (x, y y)

lim

y F (x, y)

F (x, y) F

(x, y) y

x 0

y 0

Следовательно,

для того чтобы вычислить производную функции

y f x , заданной

неявно уравнением

F x, y 0 ,

нужно приравнять нулю производную левой части как

производную сложной функции, считая

функцией

x , т.е.

y f x . При этом получим

равенство

F F y 0

или

F 0 .

Здесь

частные производные

F x, y

по переменным x и y

соответственно.

Примеры

2x 2y y

0 ,

1. x y a 0 .

y , y

0 .

2. sin x yx 0 .

0 ,

cos x y y x

sin x

cos x

y cos x

sin x

x cos x

, x 0 .

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
24.07.201785.64 Кб18Вопросы для студентов вечернего отделения от кафедры 311.pdf
#
24.07.20171.19 Mб143Лекции по Матанализу ч.3.pdf
#
24.07.20171.89 Mб395Лекции по Матанализу ч1.pdf
#
24.07.20171.2 Mб147Лекции по Матанализу ч2.pdf
#
24.07.2017166.23 Кб106Матанализ Вопросы 1 курс 1 семестр.pdf
#
24.07.2017129.01 Кб41Некоторые задачи для вечернего отделения третьего факультета от каф 311.pdf