Лабораторная работа №3
Упражнение 1.
Создать M-функцию, которая
строит в одной системе координат график
последовательности членов ряда и график
последовательности частичных сумм
ряда. При построении этой пары графиков
использовать разные цвета и маркеры. В
качестве входных параметров M-функции
использовать формулу
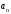общего члена последовательности и число
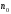рассматриваемых членов. В качестве
выходных параметров вывести значения
.
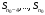Применить созданную М-функцию для
исследования следующих рядов:
1)
;
2)
;
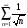3)
.
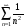function [ s1, s2, s3, s4, s5 ] = sumsPlot( f, n0 )
clf; grid on; hold on; axis equal;
% Задаём границы отрисовки
xmin = -0.5; xmax = n0;
ymin = -0.5; ymax = n0/2;
% Рисуем искиз функции
set(ezplot(f,[xmin xmax, ymin ymax]), 'Color', 'blue');
% Преобразуем строки f функции
f=str2func(strcat('@(n)',f));
% N = 0.01:0.1:n0;
% set(plot(N,subs(f,N)), 'LineWidth', 2);
s = 0;
for n=1:1:n0
s = s + f(n);
plot(n,s,'.r');
if (n == n0-4), s5 = s; end;
if (n == n0-3), s4 = s; end;
if (n == n0-2), s3 = s; end;
if (n == n0-1), s2 = s; end;
if (n == n0-0), s1 = s; end;
end;
% Рисуем оси координат
XY(xmin, xmax, ymin, ymax);
% Устанавливаем границы отображения
axis([xmin, xmax, ymin, ymax]);
end
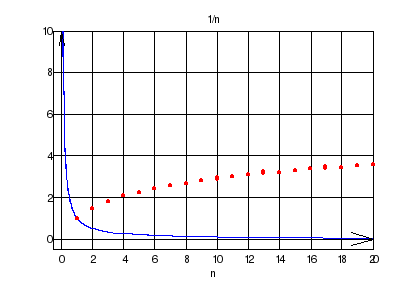
>> sumsPlot('1/n',10)
ans = 2.9290
>> sumsPlot('1/n',20)
ans = 3.5977
>> sumsPlot('1/n',30)
ans = 3.9950
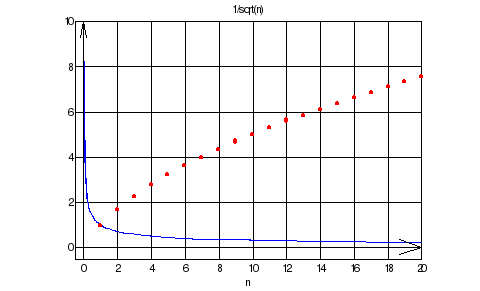
>> sumsPlot('1/sqrt(n)',10)
ans = 5.0210
>> sumsPlot('1/sqrt(n)',20)
ans = 7.5953
>> sumsPlot('1/sqrt(n)',30)
ans = 9.5851
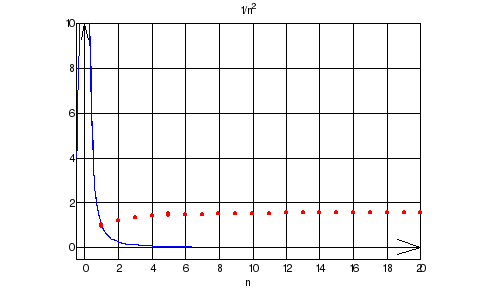
>> sumsPlot('1/sqrt(n)',10)
ans = 5.0210
>> sumsPlot('1/sqrt(n)',20)
ans = 7.5953
>> sumsPlot('1/sqrt(n)',30)
ans = 9.5851
Упражнение 2.
Установить, расходимость каких из следующих рядов можно доказать, используя необходимый признак сходимости (по Вашему желанию: «вручную» или используя MATLAB):
а)
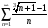б)
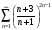
>> syms n
>> limit('((n+1)^(1/3)-1)/n', n, Inf)
ans = 0
Вывод: ряд может как сходится так и расходится
>> syms n
>> limit('((n+3)/(n+1))^(2*n-1)', n, Inf)
ans = exp(4)
Вывод: ряд расходится
Упражнение 3.
Приведите два примера расходящихся числовых рядов (отличные от рассмотренных в упр. 3), общий член которых стремится к нулю. Используя M-функцию из упр. 1, проиллюстрируйте примеры графически.
>> syms n
>> limit('1/n', n, Inf)
ans = 0
>> sumsPlot('1/n', 20)
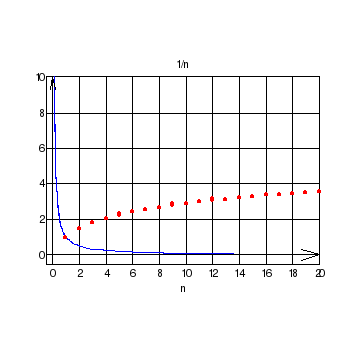
Упражнение 4.
а) Пусть ряд
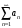сходится,
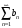расходится. Что можно сказать о сходимости
ряда
?
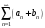Проиллюстрируйте Ваше предположение
на примере, используя М-файл из упр. 1.
>> sumsPlot('1/n + 1/n^2', 20)
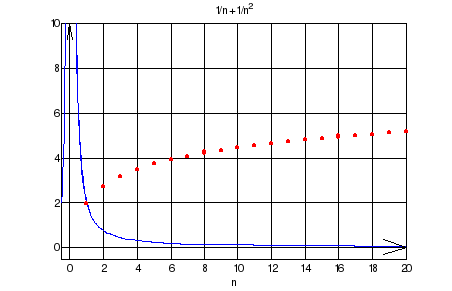
б) Пусть ряды
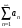и
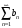расходятся. Что можно сказать о сходимости
ряда
?
Проиллюстрируйте Ваши предположения
на примерах, используя М-файл из упр. 1.
>> sumsPlot('1/sqrt(n) + 1/n', 20)
Упражнение 5.
Опираясь на признаки сходимости, доказать:
а) ряд
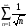расходится; б) ряд
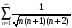сходится;
в) ряд
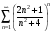расходится; г) ряд
сходится.
а) по интегральному признаку:
>> int(1/sqrt(x), 1, inf)
ans = Inf
Вывод: ряд расходится, т.к. интеграл не существует
б) ограничим ряд сверху рядом 1/n^(3/2), который сходится,
следовательно и исходный ряд сходится
в) по радикальному признаку Коши:
>> limit((((2*n^2+1)/(n^2+4))^n)^(1/n))
ans = 1/4
Вывод: т.к. 1/4 < 1, то ряд расходится
г) по интегральному признаку:
>> int(1/x*log(x)^2)
ans = log(x)^3/3
Вывод: ряд сходится
Упражнение 6.
Пусть к ряду
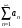применимо утверждение об оценке ряда.
Создайте M-функцию, которая
оценивает число членов, достаточное
для вычисления суммы ряда с заданной
точностью
,
и вычисляет сумму ряда с заданной
точностью. В качестве входных параметров
M-функции используйте
формулу общего члена последовательности
и точность
.
Применить созданную М-функцию для
вычисления с точностью до 0,001 суммы
ряда:
а)
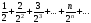б)
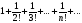
function [Sn, n] = u_6(f, epsilon)
Sn = 0;
n = 0;
while (f(n + 1) / f(n) >= 1)
n = n + 1;
Sn = Sn + f(n);
end
q = f(n + 1) / f(n);
Rn = f(n + 1) / (1 - q);
while (Rn > epsilon)
n = n + 1;
Sn = Sn + f(n);
q = f(n + 1) / f(n);
Rn = f(n + 1) / (1 - q);
end
end
>> f = @(n)(n / 2^n);
>> [Sn, n] = u_6(f, 0.001)
Sn = 1.9990
n = 14
>> f = @(n)(1 / factorial(n));
>> [Sn, n] = zad6(f, 0.001)
Sn = 1.7181
n = 6
Упражнение 7.
Создать M-функцию, которая
оценивает число членов знакочередующихся
рядов, достаточное для вычисления суммы
ряда с заданной точностью
,
и вычисляет сумму ряда с заданной
точностью. В качестве входных параметров
M-функции использовать
формулу общего члена последовательности
и точность
.
Для следующих рядов доказать сходимость и применить созданную М-функцию для вычисления с точностью до 0,001 суммы ряда:
а)
б)
.
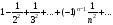function [Sn, n] = u_7(f, epsilon)
Sn = 0;
n = 0;
while (abs(f(n + 1)) > epsilon)
n = n + 1;
Sn = Sn + f(n);
end
end
>> f = @(n)((-1)^(n - 1) / n);
>> [Sn, n] = u_7(f, 0.001)
Sn = 0.6936
n = 999
>> f = @(n)((-1)^(n - 1) / n^2);
>> [Sn, n] = u_7(f, 0.001)
Sn = 0.8230
n = 31
Защита лабораторной работы
Найти сумму и определить сходимость или расходимость
-
(2n+1)/(4n^2+5)
По предельному признаку: (1/n - расходится)
>> limit(((2*n+1)/(4*n^2+5))/(1/n), n, inf)
ans = 1/2
Предел равен константе, значит ряды сходятся или расходятся одновременно, в нашем случаее расходятся
-
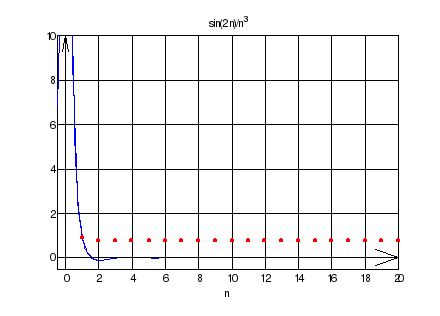
sin(2n)/n^3
Ограничиваем сверху рядом 1/n^3, который сходится, следовательно и исходный ряд сходится. Т.к. sin(2n) <= 1, то sin(2n)/n^3 <= 1/n^3
>> sumsPlot('sin(2*n)/n^3', 20)
ans = 0.8150
-
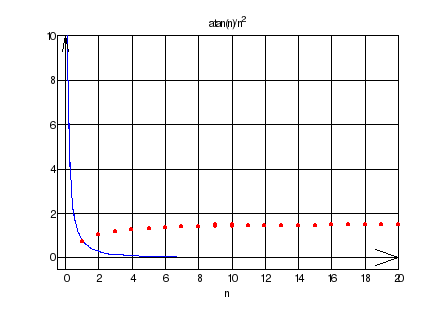
atan(n)/n^2
При n->Inf atan(n)->Pi/2, значит мы можем ограничить исходный ряд сверху 2*(1/n^2), который сходится (умножения ряда на константу не меняет его сходимость/расходимость)
atan(n)/n^2 <= 2/n^2
>> limit((atan(n)/n^2)/(1/n^2), n, inf)
ans = pi/2
>> sumsPlot('atan(n)/n^2',20)
ans = 1.5319
-