complan_problems

ÊИˆВСЬКИЙ ÍАЦIОНАЛЬНИЙ УНIВЕРСИТЕТ IМЕНI ÒАРАСА ØЕВЧЕНКА

™. Д. Бiлоколос, Д. Д. Шека

Збiрник задач з комплексного аналiзу

Навчальний посiбник

для студентiв природничих факультетiв

Êè¨â

2004

ÓÄÊ 530.145

ÁÁÊ 22.331 âåðñiÿ 2.2 (27.02.04)

™. Д. Бiлоколос, Д. Д. Шека

Збiрник задач з комплексного аналiзу: Навчальний посiбник для студентiв природничих факультетiв. К., 2004.-57 с.

Збiрник мiстить 842 задач з курсу комплексного аналiза, який автори читають на радiофiзичному факультетi Ки¨вського нацiонального унiверситета iменi Тараса Шевченка. Збiрник може бути рекомендовано студентам, аспiрантам i викладачам фiзичних та фiзико математичних спецiальностей вищих навчальних закладiв. Збiрник може бути користним також i для самопiдготовки.

°c ™. Д. Бiлоколос, Д. Д. Шека, 2003 2004

Çìiñò

Глава 1. Основнi поняття комплексного аналiзу		4
Ÿ 1.1.	Операцi¨ над комплексними числами . . . . . . . . . . .	4
Ÿ 1.2.	Способи зображення комплексних чисел . . . . . . . . .	6
Ÿ 1.3.	Добування кореня з комплексного числа . . . . . . . . .	9
Ÿ 1.4.	Функцi¨. Геометричнi i топологiчнi поняття . . . . . . .	10
Ÿ 1.5.	Елементарнi трансцендентнi функцi¨ . . . . . . . . . . .	12
Глава 2.	Аналiтичнi функцi¨	15
Ÿ 2.1.	Умови Кошi Рiмана . . . . . . . . . . . . . . . . . . . . .	15

Ÿ2.2. Геометрiчна iнтерпретацiя аналiтично¨ функцi¨ . . . . . 16

Ÿ2.3. Гармонiчнi функцi¨ . . . . . . . . . . . . . . . . . . . . . . 19

Ÿ2.4. Iнтеграл вiд функцi¨ комплексно¨ змiнно¨ . . . . . . . . . 22

Ÿ2.5. Iнтегральна теорема Кошi. Iнтегральна формула Кошi . 25

Ÿ2.6. Ряд Тейлора . . . . . . . . . . . . . . . . . . . . . . . . . 29

Ÿ2.7. Ряд Лорана, особливi точки . . . . . . . . . . . . . . . . 30

Ÿ2.8. Обчислення лишкiв . . . . . . . . . . . . . . . . . . . . . 33

Глава 3.

Застосування теорi¨ аналiтичних функцiй

36

Ÿ 3.1.

Обчислення iнтегралiв по замкнених контурах за допо-

36

могою лишкiв . . . . . . . . . . . . . . . . . . . . . . . . . .

Ÿ 3.2. Обчислення простiших визначених iнтегралiв за допомо-

38

ãîþ òåîði¨ ëèøêiâ . . . . . . . . . . . . . . . . . . . . . . .

Ÿ 3.2.2.

Iнтеграли вигляду I =

RR f(x)dx . . . . . . . . . .

40

Ÿ 3.2.1.

Iнтеграли вигляду I =

R

02¼

R(cos '; sin ')d' . . . .

38

Ÿ 3.2.3.

Iнтеграли вигляду I =

f(x)ei®xdx . . . . . . . .

42

R

R

Ÿ 3.3. Обчислення визначених iнтегралiв вiд багатозначних фун-

43

êöié . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Ÿ 3.3.2.

Iнтеграли типа I =

a

Rb

¡x

f(x)dx . . . . . . . .

44

Ÿ 3.3.1. Iнтеграли вигляду I =

R+ x®¡1f(x)dx . . . . . . .

44

Ÿ 3.4. Задача Дiрiхле. Фунцiя

R

b

¡

x

a

¢

®

¡

Ÿ 3.5.

Ãðiíà . . . . . . . . . . . . . . .

45

Конформнi вiдображення . . . . . . . . . . . . . . . . . .

47

Ÿ3.5.1. Дробово лiнiйнi функцi¨ . . . . . . . . . . . . . . 47

Ÿ3.5.2. Вiдображення елементарними функцiями . . . . . 48

Ÿ3.5.3. Вiдображення Шварца Христоффеля . . . . . . . 49

Ÿ3.6. Перетворення Лапласа. Операцiйне числення . . . . . . 51

Рекомендована лiтература	55
Абетковий покажчик	56

3

Argz =

в II та III квадрантах

в I та IV квадрантах

комплексно спряженим

рiвнi одне одному,

+ iy2

x + iy, äå x òà y дiйодиницею, тобто число,

Глава 1

Основнi поняття комплексного аналiзу

Ÿ1.1. Операцi¨ над комплексними числами

Комплексним числом називають вираз z =

снi числа, i це символ, що називають уявною квадрат якого дорiвню¹ -1, i2 = ¡1.

Два комплекснi числа z1 = x1 + iy1 i z2 = x2 ÿêùî x1 = x2 òà y1 = y2.

Комплексне число z2 = x2 + iy2 називають

äî z1 = x1 + iy1, ÿêùî x2 = x1 i y2 = ¡y1. Комплексно спряжене до числа z позначають як z. Таким чином, x + iy = x ¡ iy:

Комплексне число z можна подати також у тригонометричнiй формi z = x + iy = ½ (cos ' + i sin ') òà ó показниковiй формi z = ½ei'.

Полярний радiус ½ називають модулем комплексного числа та познача-

þòü jzj, а полярний кут ' éîãî аргументом та позначають як Argz.
значений однозначно, аргумент	jzj = p					¸ 0;
		x		+ y
На вiдмiну вiд модуля комплексного числа			2		2		ùî âè-

½arctg (y=x) + 2k¼ arctg (y=x) + (2k + 1)¼

визначений з точнiстю до будь-якого цiлого k 2 Z.

Основнi операцi¨ на множинi комплексних чисел здiйснюються таким же чином, як операцi¨ над полiномами вiдносно i:

² Сумою z1 + z2 комплексних чисел z1 = x1 + iy1 i z2 = x2 + iy2 називають комплексне число

z= z1 + z2 = (x1 + x2) + i(y1 + y2):

²Рiзницею z1 ¡ z2 комплексних чисел z1 = x1 + iy1 i z2 = x2 + iy2 називають комплексне число

z= z1 ¡ z2 = (x1 ¡ x2) + i(y1 ¡ y2):

²Добутком z1z2 комплексних чисел z1 = x1 + iy1 i z2 = x2 + iy2 називають комплексне число

z = z1z2 = (x1x2 ¡ y1y2) + i(x1y2 + y1x2):

4

1.1. Операцi¨ над комплексними числами

5

² Часткою z1=z2 вiд дiлення комплексного числа z1 = x1 + iy1 íà комплексне число z2 = x2 + iy2 6= 0 називають комплексне число

	z = z1=z2	=	x1x2 + y1y2	+ i	y1x2 ¡ x1y2	:
			x22 + y22		x22 + y22

Операцiя дiлення ма¹ змiст тiльки за умови z2 =6 0.

В прикладах 1 12 знайти дiйсну та уявну частину комплексних чисел

1 + i

z = (2 + ip

(4i + 1)5

1.

z =

5.

5)4.

p

10.

z =

:

2

¡

3i.

5.

6.

3

z = ( 7 + 3i)¡

(2 + 3i)

2.

(2 + i)2

p

p

8

11.

(2i31 + 1)3

z = i

(3 + i)2 .

7.

z = ¡ i13

2p2 3¢

.

z =

(2i + 5)2 :

+ i

3

3.

z =

i

.

(5¡+¡i)3(2

¢+ 1)2:

(1 + i)(4 ¡ 3i)3

z =

i

(3 + 4i)17

8.

12.

z =

:

(1 + i)3

i13 + 1

2

1 ¡ i

4. z =

.

9. z = µ

¶

:

(1 ¡ i)5

7i + 1

13 27 знайти модуль та аргумент комплексних чисел

В прикладахp

слiд розумiти його арифметичне значення).

(пiд коренем

¢ ¢ ¢

13.

14.

15.

16.

17.

18.

R.

19.

z = 7i:

z = ¡3:p

z = 1 + 3i:

z= ¡2 + 3i: z = 7 ¡ 3i:

z= a+ib; äå a; b 2

(p3 + ip6)6.

20.		(1 + i)8			5 :
	z¡	p
21.		= 1 +¢ cos ® +
	1 ¡ i		3
i sin ®:
22.	z	=	¡ cos ® +
i sin ®:
23.	z = sin ® + i cos ®:

24.	(5 + 2i)5.
	2 + i73p												¢	4.
										12
25.	¡	(4		¡			3i)4
26.												:
			¡		ip				3
		1						3
	¡p							p¢							¢	7
27.																	:
	¡			1	¡ ip3
			11 + i								14

В прикладахp		28 39 записати комплекснi числа у показниковiй формi
			слiд розумiти його арифметичне значення).
(пiд коренем	¢ ¢ ¢

28. z = (17 + 34i)2

29. z = (6 + i)¡3. 30. z = ¡ip5 + 4¢¡7.

31. z = ¡ip7 + p14¢3.

32. z = ¡¡p3 + i¢¡5.

33.	z =	(3 ¡ 4i)4
		(2 + 5i)3 .
		p				+ ip					7
				2				23
34.	z =	¡¡ (1 ¡ 3i)4								¢	.
35.	z =		(11i ¡ 3)8
		¡p			¡ ip				¢12 .
			15				10

можна довести нерiвнiсть

¡3 ¡ 4i

6

i + p15

36. z = ¡¡p14 + ip2¢11 .

37. z = i¡5 + ip11¢9

.

Глава 1. Основнi поняття комплексного аналiзу

¡7i7 + p15¢8

38. z = (1 + ip3)5 ¡¡p7 ¡ 3i¢3 . ¡12 + 5i3¢4

39. z = (3 ¡ 4i)7 ¡¡2 ¡ ip21¢3 .

40.Доведiть формулу Муавра (cos ' + i sin ')n = cos n' + i sin n':

Âприкладах 41 46, використовуючи формулу Муавра, записати зазначенi вирази через степенi cos ' òà sin '.

41. cos 4'.	43.		cos 7'.					45.	sin 3':		47. sin 5':
42. cos 5'.	44.		cos 9'.					46.	sin 4':		48. sin 8':
49. Довести, що µ		1 + i tg ®		¶	n		1 + i tg n®
						=				:
		1 ¡ i tg ®					1 ¡ i tg n®

50. Довести, що при будь-яких z 2 C справедлива формула jpz2 ¡ 1 +

zj + jpz2 ¡ 1 ¡ zj = jz ¡ 1j + jz + 1j:

Ÿ1.2. Способи зображення комплексних чисел

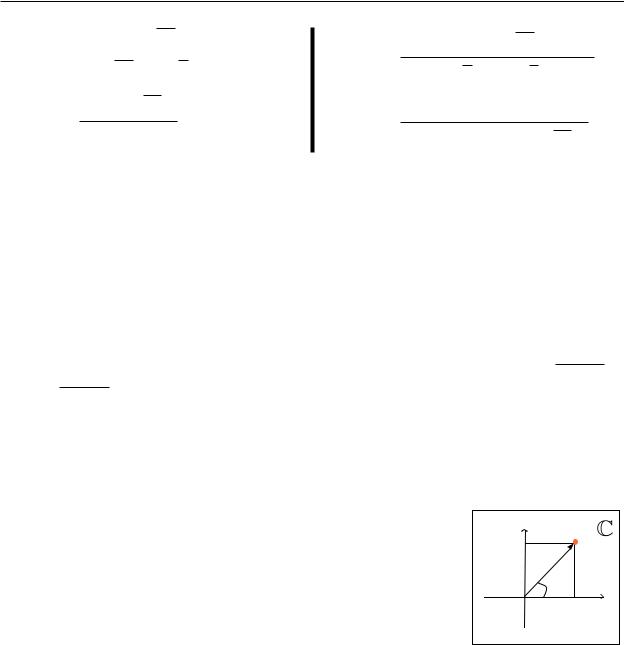
Äëÿ геометрично¨ iнтерпретацi¨ комплексне число z = x + iy зображають точкою з координата-

ìè (x; y) декартово¨ площини xOy (саму площину при цьому називають комплексною). Âiñü x будемо називати дiйсною вiссю, вiсь iy уявною. Вiд-

повiднiсть мiж множиною C та комплексною пло-

щиною ¹ вза¹мно однозначною; тому далi ми не будемо розрiзнювати термiни комплексного числа та точки комплексно¨ площини. Виходячи з тригонометрично¨ форму запису комплексного числа z,

iy	z
ρ
i	ϕ
1	x

Ðèñ. 1.1.

бачимо, що геометрично модуль ½ та аргумента ' ¹

полярними координатами радiус-вектора точки z (äèâ. ðèñ. 1.1).

Геометрiчний змiст операцiй додавання та вiднiмання поляга¹ в тому, що комплекснi числа додаються та вiднiмаються таким же чином, як i вектори (див. рис. 1.2). Виходячи з геометрично¨ iнтерпретацi¨, для будь-яких двох комплексних чисел z1 òà z2

трикутника

jjz1j ¡ jz2jj · jz1 + z2j · jz1j + jz2j:

Однак, слiд зазначити, що при операцiях множення та дiлення комплекснi числа виконують обов'язкi лiнiйних операторiв. Геометрично множення комплексного числа z на комплексне число z1 = ½1ei'1 зводиться

1.2. Способи зображення комплексних чисел						7
до повороту вектора z íà êóò '1 та змiни його довжини в ½1 разiв, тобто
z ми розгляда¹мо як вектор, а z1 як лiнiйний оператор, що дi¹ на цей
вектор (або навпаки).
У зв'язку з цим бува¹ корисною матричне зо-
zбраження= x + iy можекомплекснихбути ототожненочисел: комплекснез матрицеючислодру-				iy
				z +z
гого порядку, що ма¹ спецiальний вигляд				1	2
				z2
z = °¡y		x°:			z - z
					1	x
°	x	y	°		z1
°			°
°			°

При такому ототожненi алгебра¨чнi операцi¨ дода-

Ðèñ. 1.2.

вання, вiднiмання, множення та дiлення виконую-

ться за звичайними правилами матрично¨ алгебри.

В прикладах 51 77 зобразити на C-площинi множину точок M.

51.

M =

z

: z

a

= R

, äå a

64. M = ½z

z

¡

a

= 0¾, äå

C, R 2 R+f:

j

¡

j

g

2

: Im

z

¡ b

52. M = fz

: jz ¡ aj < Rg, äå a 2

a; b 2 C:

C, R 2 R+:

: jz ¡ ij > 4g.

65. M =

z1; z2; z3

:

z1

j

= z2

j

=

53. M = fz

.

jz3j = 1,

n

j

j

54. M =

f

z

: z + 1

¡

2i

< 3

g

z1 + z2 + z3 = 0 :

55.

j

j

,

M=fz : jz ¡ z1j + jz ¡ z2j = Rg

66. M =

z

Im

z = 0 :

äå z1; z2 2 C, R 2 R+:

67. M=

f

z

1

z

2i

g

f

z :

jj

¡

j ¡ j

¡

jj

=6 :

56. M = fz

: jz ¡ ij + jz + ij < 5g.

g

68.

M =

z

:

Re

z

¡

1

= 0

:

57.

M = fz.

: jz ¡ z1j = jz ¡ z2jg,

äå

½

z + 2i

¾

z1; z2 2 C

69. M =

f

z

: 2 z

j

< 1 + Im z

g

:

58.

M = fz

: ® < arg(z ¡ z0) < ¯g

,

70. M =

:

j

Re z

f

z

z

> 1

¡

g

:

äå z0

2 C

, ®; ¯

+:

j j

2 R z + i

¾

71.

M =

½z :

Re

z + 2i

= 1¾.

59. M =

z

: Im

= 0

:

z + 1

z + 7i

½

i ¡ z

72. M = ½z

: Im

z + 2

= 0¾.

60. M =

z

: 0 < arg

< ¼2

:

z + i

½

z

z

1

i + z

¾

73. M =

z

: Re

z ¡ a

= 0

61.

M = z

:

¯z

¡

¯

= a;

,

äå

½

z + a

¾,

äå

z1; z2

½

¡

z2

¾

a

2

R+.

2 C

, a

2 R

+¯

:

¯

z

:

z

a

z

b

= 1

;

¯

z

¯

74. M =

f

jj

¡

j ¡ j

¡

jj

g

¯

¯a

62. M = ½z : Re

¡

= 0¾,

äå

äå a; b 2 C.

z

b

z

a

a; b

2 C

:

¡

75. M =

z

: Im

¡

= 0

63.

Re

1=z < 1=2g :

a 2 N:

½

z + a

¾, äå

M = fz :

8				Глава 1. Основнi поняття комплексного аналiзу
	M = ©z :	2	< arg(z ¡ 2i)	< ¼ª. 77. M = ½z : Im		2		z¡+ i	= 0¾:
76.		¼	2				z	1 + i

78. Виходячи з геометрично¨ iнтерпретацi¨ комплексних чисел, довести нерiвнiсть jz1 + z2j · jz1j + jz2j: Довести зазначену нерiвнiсть також алгебра¨чним шляхом.

79. Виходячи з геометрично¨¯¯ iнтерпретацi¨¯¯ комплексних чисел, довести нерiвнiсть jz1 ¡ z2j · ¯jz1j ¡ jz2j¯: Довести зазначену нерiвнiсть також

алгебра¨чним шляхом.

80. Виходячи з геометрично¨ iнтерпретацi¨ комплексних чисел, довести
íåðiâíiñòü	¯jzzj		¡ 1¯	· j arg zj:
	¯		¯
	¯		¯

81.Виходячи з геометрично¨¯¯ ¯¯ iнтерпретацi¨ комплексних чисел, довести

íåðiâíiñòü jz ¡ 1j · ¯jzj ¡ 1¯ + jzjj arg zj:

82.Нехай z1 + z2 + z3 = 0 òà jz1j = jz2j = jz3j = R. Довести, що точки

z1; z2; z3 ¹ вершинами правильного трикутника, що вписаний в коло jzj =

R.

83.Нехай точки z1; z2; z3 знаходяться на колi з центром в точцi 0. Довести, що трикутник з вершинами в точках z1; z2; z3 ¹ правильним тодi i ëèøå òîäi, êîëè z1 + z2 + z3 = 0.

84.Довести, що комплекснi числа z1; z2; z3 знаходяться на однiй прямiй, якщо вони задовольняють умовам z2 ¡ z1 2 R:z ¡ z ;

3 1

	85. Довести, що комплекснi числа z1; z2; z3; z4 лежать на колi, якщо вони
	z2	¡ z1	:	z2 ¡ z4		:
	задовольняють умовам z3				2 R
		¡ z1		z3 ¡ z4;

86.Нехай z1 6= z2 6= z3. За яко¨ умови точки z1, z2, z3 знаходяться на îäíié ïðÿìié?

87.Нехай z1 6= z2 6= z3 6= z4. За яко¨ умови точки z1, z2, z3, z4 знаходяться на одному колi або прямiй?

88.З'ясувати змiст комплексного числа z як лiнiйного оператора.

89.Виходячи з матрично¨ iнтерпретацi¨ комплексних чисел, знайти матричне зображення операцi¨ комплексного спряження.

90.Виходячи з матрично¨ iнтерпретацi¨ комплексних чисел, знайти матричне зображення модуля комплексного числа.

91.Виходячи з матрично¨ iнтерпретацi¨ комплексних чисел, знайти матричне зображення комплексного числа 1=z.

92.Виходячи з матричного зображення комплексних чисел, з'ясувати змiст операцi¨ множення комплексних чисел. Обчислити, використовую-

1.3. Добування кореня з комплексного числа

9

чи матричне зображення, наступний добуток: (2 + 3i)(¡1 + ip3).

93. Виходячи з матричного зображення комплексних чисел, з'ясувати
змiст операцi¨ дiлення комплексних чисел. Обчислити, використовуючи
матричне зображення, наступну частку:				1 ¡ i
				1 + i.			°¡ sin ' cos '°
94. Довести, що для будь-яко¨ унiтарно¨ матрицi U =
							°	cos '		sin '	°
викону¹ться спiввiдношення Un	=		cos n'		sin n'		n°	2 N	.		°
		°¡ sin n'			cos n'°, äå		°				°
		°				°
		°				°
		°				°

Ÿ1.3. Добування кореня з комплексного числа

Показникова форма запису комплексного

операцiйчисла ¹ зручноюпiднесенняпри дорозгляданнiстепеня таалгебра¨чнихдобування

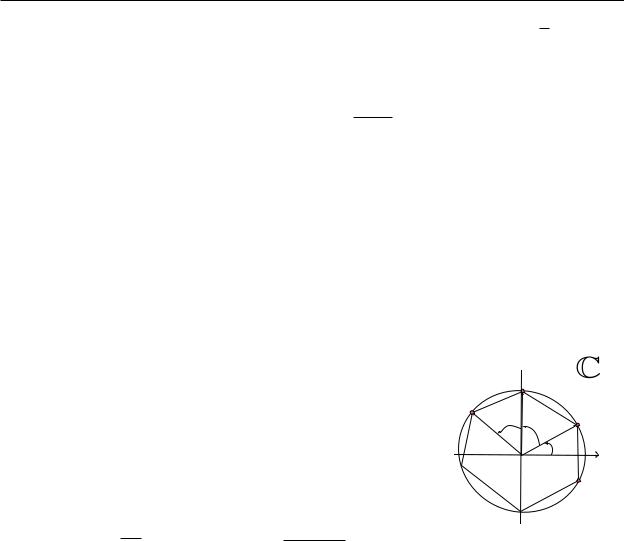
кореня. Так, якщо z = z1n, òî ½ = ½n1 , ' = n'1. Комплексне число z1 назива¹ться коренем n-го степеня комплексного числа z, ÿêùî z = z1n.

Алгебра¨чне рiвняння zn = a, äå a ´ jajei® 2

C, n 2 N ì๠ïðè a 6= 0 ðiâíî n рiзних коренiв, що визначаються за формулою

p

zk = n jajei(®+2¼k)=n; k = 0; n ¡ 1:

y

z

1

z

2

2π	2π		z
−				0
n
	−n
		α		x
		−
		n
			z
				n-1

Ðèñ. 1.3.

На комплекснiй площинi коренi рiвняння
zn = a зображуються точками, розташованими у вершинах правильно-
координат (див. рис. 1.3).	p
		j		j
ãî n-кутника, що ¹ вписаним у коло радiуса	n		a		з центром у початку

Для того, щоб вiдрiзняти дiйсне значення коренi n-то ступеня вiд

додатнього числа a òà n êîìïлекних значень, надалi позначатиме дiйснi (алгебра¨чнi) значення як pn a, комплекснi значення як z1=n.

В прикладах 95 104 обчислити усi значення кореня комплексного

числа z.

95.

z = i1=3.

z = (7 +

8i)

1=5.

102.

z = (2 ¡ 3i)

1=5.

99.

96.

z = (3i + 1)1=4.

1=3.

97. z = (3i

¡

4)2=3.

100. z = (11

¡ 4i)

1=4.

103.

z = (2 ¡ 3i)1=5.

98.

101. z = (¡2 + 3i)

104.

z = (

5

2i)1=7

.

z = (2i)1=4.

¡

¡

10 Глава 1. Основнi поняття комплексного аналiзу

105. Довести, що для будь-якого комплексного числа z = x+iy значення функцi¨ z1=2 дорiвнюють:

2s

+ isignys

3

(x + iy)1=2 = §

p

+ x

p

¡ x

:

x2

+2y2

x2 +2y2

4

5

В прикладах 106 136, використовуючи результат задачi 105, знайти усi значення виразiв:

106. (2i)1=2.

(11 ¡ 60i)1=2.

127.

(45 ¡ 28i)1=2.

117.

107. (1 ¡ i)1=2.

118. (20 + 48i)1=2.

128.

(16

¡

30i)1=2.

108. (3 ¡ 4i)1=2.

.

119. (27 ¡ 36i)1=2.

129.

(24

10i)1=2.

109. (¡40 + 42i)1=2

120. (

¡

9

¡

40i)1=2.

130. (32

¡

24i)1=2.

110.

(¡5 + 12i)

1=2.

¡

1=2.

121.

(35 ¡ 12i)1=2.

131.

(45

¡

28i)1=2.

111.

(¡48 ¡ 14i)

122.

(120 + 182i)1=2.

132.

(60

32i)1=2.

112. (¡11 ¡ 60i)1=2.

123. (24

¡

70i)1=2.

133.

¡

p

1=2.

(

3i)

113.

1=2.

1

4

¡ ¡p

(7 + 24i)

.

124. (1 + i2p2)1=2.

134.

1=2.

114.

(29

420i)1=2

1=2.

(4 ¡ 2

5i)

¡

125. (

12 + i4p7)

1=2.

¡

135.

p

1=2.

115.

(¡13 ¡ 84i)

126.

p

1=2.

(3 ¡ 2

10i)

.

116.

13)

( 9

40i)1=2.

(¡4 + i6

136. (21

¡

220i)1=2

¡ ¡

В прикладах 137 151, знайти всi розв'язки рiвнянь:

137. z3 = 1.				142.
138.	z2	= ¡63 + 16i.		143.
139.	z7	= 3 + 4i:		144.
140. z8 + 1 ¡ i = 0:				145.
141. 4z2 + 9(1 + i) = 0:				146.

z3	= ¡11 ¡ 2i:		147. (¡2+3i)z7 = ¡1:
z5 + 3 ¡ 4i = 0:			148.	(1¡4i)z3 = 2+3i:
z4	= ¡7 ¡ 24i:		149.	5(4 + 3i)2z8 = 1:
z5	= 41 ¡ 38i:		150.	jzj ¡ z = 3 + 4i.
z7	= 8 ¡ 8i:		151.	z¹ = zn, äå n 2 N.

152.	Знайти комплекснi числа z1; z2; ÿêùî z1 +z2 = 4+4i; z1z2 = 8+14i:
153.	Скiльки значень ма¹ вираз zn=m, äå z 2 C; n; m 2 N; m 6= 0?

Ÿ1.4. Функцi¨. Геометричнi i топологiчнi поняття

На множинi M точок площини C задано комплексну функцiю комплексно¨ змiнно¨ w = f(z), якщо задано закон, за яким кожнiй точцi z ç M ставиться у вiдповiднiсть задана точка w з множини N. При цьому множину M називають множиною визначення, а множину N множиною значень. Якщо кожному значенню z 2 M вiдповiда¹ одне значення