
Задачник / Глава 04 (81-99)
.pdf
Глава 4 Геометрические характеристики площади плоских фигур
4.1 Теоретическая и методическая информация. Примеры
4.1.1 Основные понятия
Геометрическими характеристиками сечения являются площадь сечения А, статические моменты площади относительно координатных осей Sx , S y , моменты инерции плоской фигуры – осевые I x , I y , центробеж-
ный I xy , полярный I p (рис. 4.1):
A dA;
A
Sx ydA;
A
S y xdA;
A
Ix y2dA;
A
I y x2dA;
A
Ixy xydA;
A
I p 2dA.
A
y
хdA
y
0 |
х |
Рис. 4.1
4.1.2 Определение положения центра плоской фигуры
Общий случай:
|
|
|
n |
|
|
|
n |
|
|
|
|
|
Ai yci |
|
|
|
Ai xci |
|
|
y |
|
|
i 1 |
; x |
|
|
i 1 |
, |
|
c |
n |
c |
n |
||||||
|
|
|
|
|
|||||
|
|
|
Ai |
|
|
|
Ai |
|
|
|
|
|
i 1 |
|
|
|
i 1 |
|
где n – число простых фигур, на которые разделено сечение;
Ai , xci , yci – площадь и координаты центров каждой из фигур; xc , yc – координаты центра всего сечения.
Частные случаи
1.Если сечение имеет две оси симметрии, то центр тяжести площади размещается в точке пересечения осей симметрии.
2.Если сечение имеет только одну ось симметрии, то центр тяжести фигу-
ры лежит на этой оси и определять надо только одну координату – y c или xc . 3. Если выделить две части сечения, то их общий центр тяжести будет
81
лежать на прямой, соединяющей центры тяжести этих двух частей, и будет делить эту прямую на отрезки, по длине обратно пропорциональные площадям составляющих фигур.
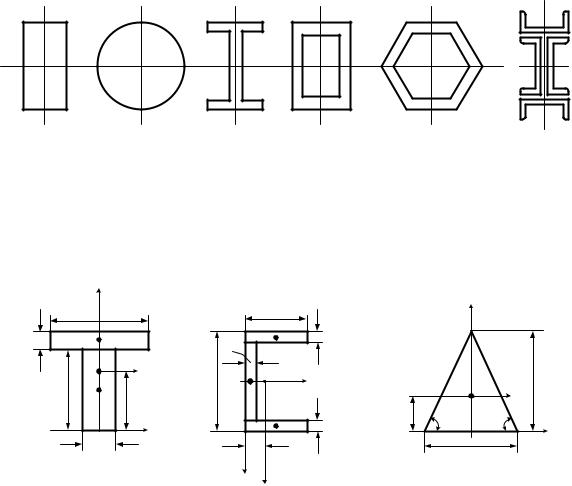
Пример 4.1.1. Найти центр тяжести заданных сечений (рис. 4.2).
Рис. 4.2
Решение. Все эти сечения имеют центр тяжести в точке пересечения осей симметрии.
Пример 4.1.2. Найти центр тяжести заданных сечений (рис. 4.3).
а) |
y0 |
|
|
|
|
12 см |
|
2 |
C1 |
|
|
10 |
C |
|
x0 |
C2 |
yc |
|
|
|
4 см |
х |
|
|
|
||
б) |
|
|
|
|
|
|
10 см |
|
|
|
|
|
|
2 |
см |
2 |
C1 |
|
|
|
|
x0 |
|
|
22 |
C2 |
C |
|
|
|
|
|||
|
|
C3 |
|
2 |
|
|
|
|
|
|
|
xC |
|
|
|
y |
у0 |
|
|
|
|
Рис. 4.3 |
|
|
|
в) |
y0 |
|
|
|
|
|
|
|
|
h |
|
|
C |
x0 |
уC |
|
|
|
|
|
||
|
|
b |
х |
Решение. Во всех сечениях одна ось симметрии, поэтому для определения положения центра тяжести фигуры в каждом случае необходимо вычислить только одну координату:
а) y |
|
|
A1 yc1 |
A2 yc2 |
|
24 11 40 5 |
7,25 см; |
c |
|
|
|
||||
|
|
A1 |
A2 |
|
24 40 |
||
|
|
|
|
||||
б) x |
A1xc1 A2 xc2 A3 xc3 |
|
|
20 5 36 1 20 5 |
3,10 см; |
|||
|
|
|
|
|||||
c |
A1 A2 A3 |
|
|
20 36 20 |
||||
|
|
|
||||||
в) из геометрии известно, что центр треугольника располагается на |
||||||||
расстоянии 1/3 высоты от основания |
y |
|
|
1 |
h . |
|||
c |
|
|||||||
|
|
|
|
3 |
|
|||
|
|
|
|
|
|
|||
82

Пример 4.1.3. Найти центр тяжести фигуры (рис. 4.4).
Решение. A1 300 см2;
A2 600 см2. Соединяем центры тяжести первой и второй фигур прямой C1C2 . С – общий центр тяжести.
30 см |
C1 |
|
|
|
C2 |
|
|
|
C |
15 |
|
|
|
||
|
10 |
40 см |
|
Рис. 4.4
CC1 |
|
A2 |
|
600 |
2; |
CC |
2 |
C C |
; CC |
|
1 |
C C |
. |
|
|
|
|
|
|||||||||
CC |
|
A |
|
300 |
|
1 |
3 1 2 |
2 |
3 1 2 |
|
|||
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Этот прием определения положения центра тяжести удобен не столько для точных расчетов, сколько для ориентировочной оценки места нахождения центра тяжести.
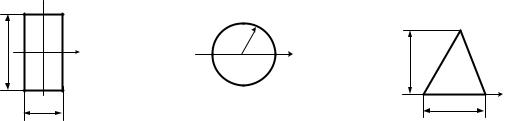
Пример 4.1.4. Найти центр тяжести фигуры (рис. 4.5).
Решение. 1. Делим фигуру на |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
три простые составные части A i – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
два прямоугольника и треугольник. |
|
|
|
|
xC |
у |
|
|
|
|
C |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2. Выбираем оси x и y и на- |
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ходим координаты центров тяжести |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|||||
10 |
|
|
|
|
|
|
yC |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
каждой |
из |
трех |
частей |
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
( xci , yci , |
i 1, 2, 3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
20 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||||||
3. |
Подсчитаем координаты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
центра |
тяжести |
всей |
фигуры |
|
|
|
|
|
|
|
Рис. 4.5 |
|
|
||||||||||||
( xc , yc ). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчеты сведены в таблицу 4.1.
15 |
|
см |
|
|
25 |
|
||
|
|
|
х
|
|
|
|
|
Т а б л и ц а 4.1 |
|
|
|
|
|
|
|
|
i |
A i, |
xci, |
yci, |
Aixci, |
Aiyci, |
|
|
см2 |
см |
см |
см3 |
см3 |
|
1 |
200 |
10 |
5 |
2000 |
1000 |
|
2 |
125 |
22,5 |
12,5 |
2812,5 |
1562,5 |
|
3 |
75 |
28,3 |
20 |
2122,5 |
1500 |
|
|
3 |
|
|
S y 6935 |
|
|
|
Ai 400 |
|
|
Sx 4062,5 |
|
|
|
1 |
|
|
|
|
|
83
y |
|
|
Sx |
|
Ai yci |
|
4062,5 |
10,16 см; |
|||||
c |
|
|
|
|
|
||||||||
|
|
|
A |
|
Ai |
400 |
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
x |
|
|
S y |
Ai xci |
6935 |
17,34 см. |
||||||
|
|
|
|
||||||||||
|
c |
|
|
A |
|
Ai |
400 |
|
|
||||
|
|
|
|
|
|
|
|
||||||
Проверка. Известно, что статические моменты площади относительно осей, проходящих через центр тяжести фигуры, равны нулю.
3
Sx0 Ai yci yc 200 (5 10,16) 125 (12,5 10,16)
1
75 (20 10,16) 1,5 см3;
3 |
|
|
|
|
|
S y0 Ai xci xc 200 |
(10 |
17,34) |
125 (22,5 |
17,34) |
|
1 |
|
|
|
|
|
75 (28,3 17,34) 1 см3. |
|
|
|||
Если учесть, что слагаемыми при вычислении Sx0 и S y 0 были трех-,
четырехзначные числа, то можно считать, что полученные суммы – статические моменты площади заданной фигуры относительно осей x0 и y0 –
практически близки к нулю. Следовательно, оси x0 и y0 действительно проходят через центр тяжести фигуры.
4.1.3 Моменты инерции плоских фигур. Расчетные формулы
Моменты инерции простейших фигур (рис. 4.6–4.8)
y
h |
х |
r |
|
|
|
||
|
х |
h |
|
|
|
b |
b |
х |
I |
|
|
bh3 |
; I |
|
|
hb3 |
I |
|
|
r4 |
; I |
|
|
r4 |
I |
|
|
bh3 |
|
x |
12 |
y |
12 |
x |
4 |
p |
2 |
x |
12 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Рис. 4.6 |
|
|
|
|
|
Рис. 4.7 |
|
|
|
Рис. 4.8 |
|||||||
Заметим, что для треугольника момент инерции определяется по приведенной формуле относительно оси, проходящей через основание, а
84
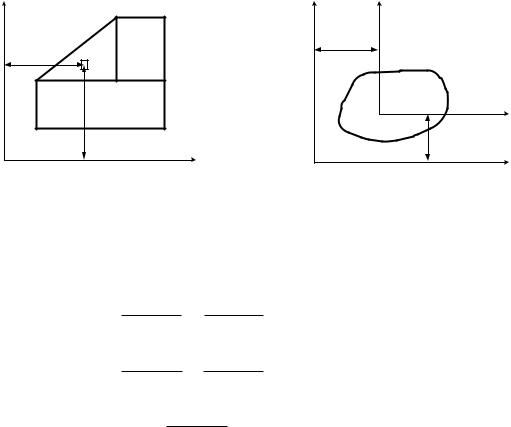
для прямоугольника и круга – относительно осей, проведенных через |
||||||||||||||||||||
центр тяжести фигур. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Моменты инерции площади сложной фигуры определяются как ал- |
||||||||||||||||||||
гебраическая сумма соответствующих моментов инерции относительно за- |
||||||||||||||||||||
данных осей простейших фигур, на которые можно разделить исходную |
||||||||||||||||||||
сложную фигуру (рис. 4.9): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
I x I xi ; |
I y I yi ; I xy |
I xyi , |
|||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
i |
|
|
|
i |
|
|
|
где i – порядковый номер частей, на которые разделена фигура. |
||||||||||||||||||||
Моменты инерции плоской фигуры относительно осей, параллель- |
||||||||||||||||||||
ных центральным осям (рис. 4.10): |
|
|
|
|
|
|
|
|
|
|
||||||||||
I |
x1 |
I |
x |
a2 A; |
I |
y1 |
I |
y |
b2 A; |
I |
x1y1 |
I |
xy |
abA, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где A – площадь фигуры; а и b – координаты центра тяжести площади С в |
||||||||||||||||||||
осях x1, y1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
|
|
|
y |
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
х |
|
|
dА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
0 |
|
|
|
|
|
|
|
|
х |
|
|
|
|
0 |
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.9 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.10 |
||||||
Моменты инерции |
|
плоской |
|
фигуры |
относительно |
повернутых осей |
||||||||||||||
(рис. 4.11): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
x1 |
I x |
I y |
I x |
I y |
cos 2 I |
xy |
sin 2 ; |
||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
I |
y1 |
I x |
I y |
I x |
I y |
cos 2 I |
xy |
sin 2 ; |
||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
I |
x1y1 |
I x |
I y sin 2 I |
xy |
cos 2 , |
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
положительно при повороте осей против часовой стрелки. |
||||||||||||||||||||
85
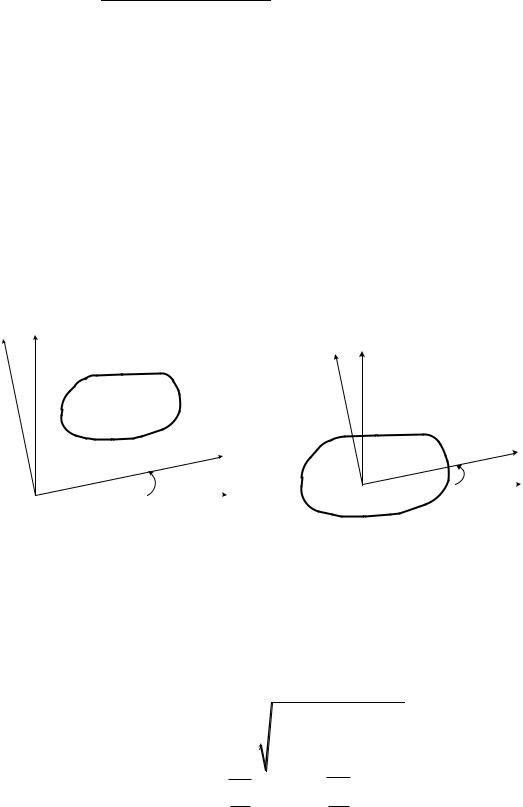
Определение положения главных осей, величины главных моментов инерции I xг , I yг и радиусов инерции ix , iy
Главные центральные оси инерции плоской фигуры – это такие оси, которые проходят через центр тяжести фигуры и относительно которых
осевые моменты инерции достигают экстремальных значений и
I y min , а центробежный момент инерции фигуры относительно этих осей обращается в ноль. I x max и I y min называют главными моментами инер-
ции. Если известны моменты инерции I x , I y , I xy относительно некото-
рой центральной координатной системы х, у, то найти угол наклона 0 главных осей инерции xг , yг и величины главных моментов инерции I x г
и I y г (рис. 4.12) можно, воспользовавшись последними тремя формулами для случая поворота осей.
y1 |
y |
y |
|
|
yГ |
|
|
|
|
|
х1 |
|
|
|
|
|
|
C |
|
|
|
|
0 |
хГ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
х |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рис. 4.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.12 |
|
|
|||
Принимая I x1, y1 = 0, находим |
tg2 0 |
|
2I xy |
, а из формул для |
||||||||||||||||||
I x I y |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
I x1 и I y1 можно при 0 получить зависимости: |
|
|
|
|||||||||||||||||||
|
Ixг |
|
I |
x |
I |
y |
|
|
|
I |
x |
I |
y |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ixy2 ; |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
I yг |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
ix 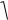
 IAx ; iy
IAx ; iy 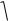
 IAy .
IAy .
86
4.1.4 Определение моментов инерции как алгебраической суммы моментов инерции простейших фигур
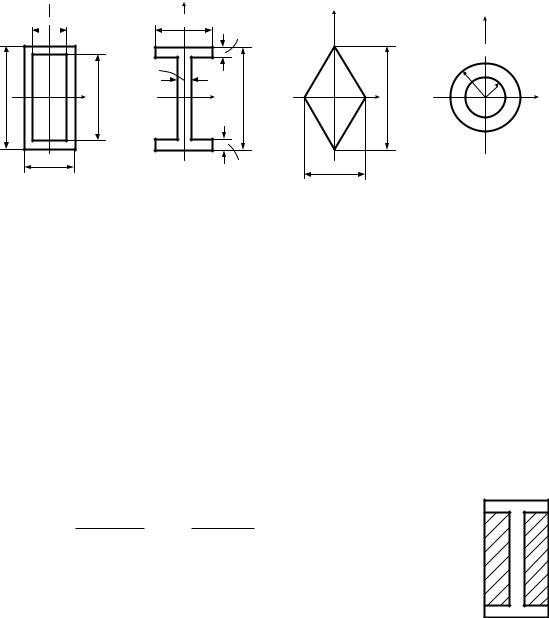
Пример 4.1.5. Найти момент инерции относительно главной центральной оси x (рис. 4.13).
а)
H=20 см
 y b=10 см
y b=10 см
х
В=12 см
|
б) |
y |
|
в) |
y |
г) |
|
|
y |
|
b=12 см |
|
|
|
|||||
|
|
t=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
0с |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
R= |
|
|
h=18 см |
t=2 |
|
h=20 см |
|
|
h=20 см |
|
|
r=5 см |
|
|
|
|
|
|
||||
|
х |
|
х |
|
|
х |
|||
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
b=12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.13 |
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а) I x |
|
|
BH |
3 |
|
bh3 |
|
12 203 |
|
10 183 |
|
3140 см4; |
|||||
12 |
|
12 |
|
12 |
|
12 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) I |
|
|
bh3 |
b t h 2t 3 |
|
12 203 |
|
|
10 163 |
4587 см4. |
|||||||
x |
|
|
|
|
|||||||||||||
|
|
12 |
|
|
|
12 |
|
12 |
12 |
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
Момент инерции I x подсчитан как разность моментов инерции опи-
санного прямоугольника и двух заштрихованных прямоугольников
(рис. 4.14).
|
|
|
|
b(h / 2)3 |
|
12 203 |
||
в) |
I x |
|
12 |
2 |
2 2000 см4. |
|||
|
|
|
|
|
|
12 |
||
Момент инерции |
I x |
подсчитан как сумма моментов |
||||||
инерции верхнего и нижнего треугольников относительно |
||||||||
оси x. |
|
|
|
|
|
|
|
|
|
|
|
R |
4 |
|
4 |
Рис. 4.14 |
|
г) |
I |
x |
|
r |
|
104 54 7363 см4. |
||
|
|
|
4 |
|
4 |
|
4 |
|
|
|
|
|
|
|
|||
87
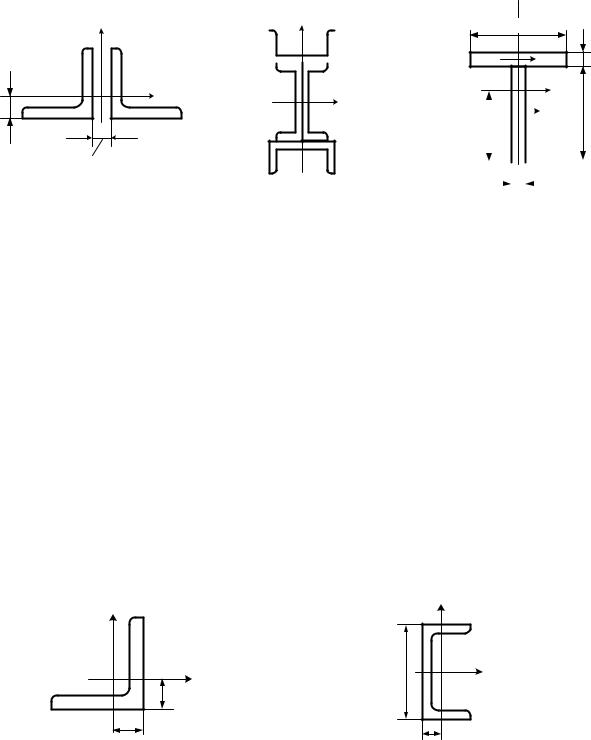
4.1.5 Определение моментов инерции сечений с помощью формул перехода к параллельным осям
Пример 4.1.6. Найти моменты инерции сечений относительно центральных осей x, y (рис. 4.15).
z 0
а) |
y |
б) |
|
y |
4 [ 16 |
|
|
||||
|
|
||||
|
|
|
|
|
|
х
х
а=4 см
2∟100×100×10
Рис. 4.15
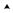 y
y
в) |
12 |
2 |
|
|
х1 |
|
|
х |
см |
|
|
|
|
|
|
|
|
х2 |
см |
|||
|
|
|
|
|
|||||||||
9,5 |
|
|
|
|
|
|
|
|
|
|
12 |
||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. В приведенных сечениях собственные центральные оси составляющих частей сечения параллельны главным центральным осям всего сечения. Моменты инерции частей фигуры относительно собственных центральных осей могут быть взяты из сортаментов прокатной стали (прил. I–III) или легко подсчитаны. Следовательно, для вычисления моментов инерции относительно главных центральных осей всего сечения достаточно воспользоваться формулами перехода к параллельным осям.
а) Из сортамента «Сталь прокатная уголковая равнополочная по
ГОСТ 8509-86» выписываем необходимые данные об уголке
∟100 100 10 (рис. 4.16):
I x1 179 см4; |
|
A 19,2 см3; |
z0 2,83 см. |
|
|||||||||
Тогда (рис. 4.15, а) I x |
2I x1 2 179 358 см4; |
|
|||||||||||
I |
|
|
I |
|
A z |
|
|
a |
2 |
2 179 19,2 4,832 2 1254 |
см4. |
||
y |
x1 |
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
y1 |
|
|
|
х |
1 |
h |
х1 |
|
|
|
|
z0 |
|
|
|
z0 |
|
|
|
|
|
|
z0 |
Рис. 4.16 |
|
|
Рис. 4.17 |
88
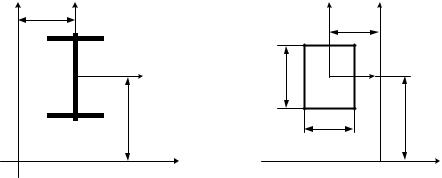
б) Из сортамента «Сталь горячекатаная. 89)»: [16 (рис. 4.17); I x1 747 см4; I y1
A 18,1см2.
Тогда в соответствии с рисунком 4.15, б:
Швеллеры (по ГОСТ 8240-63,3 см4; z0 1,80 см;
|
|
|
|
|
|
|
|
|
h |
2 |
|
2 747 2 63,3 18,1 |
|
2 |
5097 |
4 |
I x 2I x1 2 I y1 |
A z0 |
|
|
|
|
9,8 |
|
см ; |
||||||||
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 I |
|
|
|
|
|
|
|
|
|
|
|
|
I |
y |
2I |
x1 |
y1 |
Az2 |
2 747 2 63,3 18,1 1,82 1738 см4. |
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
в) Делим тавр на два прямоугольника. Замечаем, что они раны по размерам и по площади. Общий центр тяжести сечения, следовательно, расположен посередине между центрами составляющих прямоугольников, т.е. на расстоянии 9,5 см от нижнего края и по 3,5 см от оси х до осей х1 и х2:
I x |
|
12 23 |
12 2 |
3,5 2 |
2 123 |
12 2 3,5 2 |
884 см4; |
||||||
|
12 |
|
12 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 123 |
|
12 23 |
|
|
|
||||
I y |
|
|
|
|
|
|
|
|
|
296 см4. |
|
|
|
12 |
|
12 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
Пример 4.1.7. Найти моменты инерции сечения относительно заданных осей (рис. 4.18).
а) |
y |
b=10 |
y0 |
б) |
y0 |
y |
|
|
|||||
|
|
|
№ 10 |
|
b 10 |
|
|
|
|
|
|
|
|
|
|
|
x0 |
см |
|
|
|
|
|
h=12 |
|
см |
|
|
|
|
см |
x0 |
||
|
|
|
|
|
|
|
|
|
|
а=20 |
|
c=10 cм |
а=15 |
|
|
|
|
|
|
|
|
0 |
|
х |
|
|
х |
|
|
|
Рис. 4.18 |
|
|
|
Решение. Собственные главные центральные оси инерции сечения параллельны заданным осям x, y. При расчетах используем форму-
лы перехода к параллельным осям.
а) Из сортамента ГОСТ 8239-89 для I 10: I x0 198 см4;
|
|
I y0 |
17,9 см4; |
A 12 см2; |
|
I |
x |
I |
x0 |
a2 A 198 12 202 4998 см4; |
|
|
|
|
|
||
89
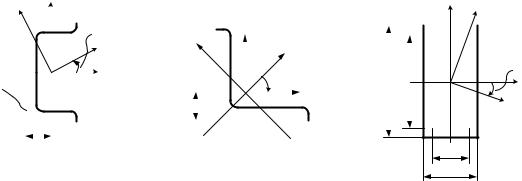
I y I y 0 b2 A 17,9 12 102 1217,9 см4;
Ixy Ix0 y0 abA 0 12 10 20 2400 см4.
б) Для прямоугольника:
|
|
|
|
|
I |
|
|
|
ch3 |
|
; I |
|
|
hc3 |
; I |
|
|
0 ; |
|||||
|
|
|
|
|
x0 |
|
y0 |
|
|
x0 y0 |
|||||||||||||
|
|
|
|
|
|
12 |
|
|
|
|
|
12 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 123 |
|
|
|
|
||||||
|
I |
x |
I |
x0 |
a2 A |
|
|
|
|
|
|
152 12 10 28440 см4; |
|||||||||||
|
|
|
12 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
12 103 |
|
|
|
|
||||||||
I |
y |
|
I |
y0 |
b2 A |
|
|
|
|
|
|
|
( 10)2 |
12 10 13000 см4; |
|||||||||
|
|
|
12 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ixy |
Ix0 y0 |
abA 0 (15) ( 10) 12 10 18000 см4. |
|||||||||||||||||||||
4.1.6 Определение моментов инерции с использованием формул перехода к повернутым осям
Пример 4.1.8. Найти момент инерции сечений относительно осей x,
y (рис. 4.19).
а) |
y |
|
|
|
|
y0 |
б) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
y0 |
|
|
y |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
х |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
х0 |
|||||||
|
|
|
|
|
|
|
|
|
х0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
|||
№ 20 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
z0 |
|
|
|
|
|
|
|
|
|
140 140 12 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
в) |
|
|
|
|
|
y0 |
y |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
20 см |
|
18 см |
|
|
|
|
||
|
|
|
|
|
||||
|
|
|
|
|
х0 |
|||
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
12 |
Рис. 4.19
Решение. Моменты инерции сечения относительно главных центральных осей x0 , y0 берем из сортамента или подсчитываем.
а) Швеллер №20; I |
x0 |
1520 |
см4; |
I |
y0 |
113 |
см4; |
30o , |
|
|
|
|
|
|
|
I x0 y0 0.
I |
|
|
I x0 I y0 |
|
I x0 I y0 |
cos 2 I |
|
sin 2 |
x |
|
|
x0 y0 |
|||||
|
2 |
2 |
|
|
||||
|
|
|
|
|
||||
90
