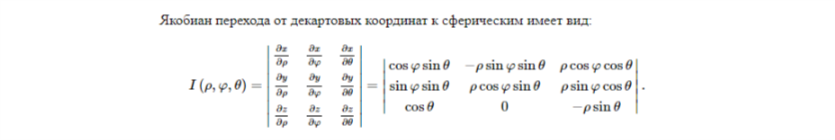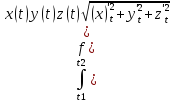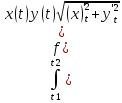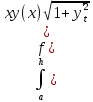Основные свойства двойного интеграла

Свойство 1. Постоянный множитель можно вынести за знак двойного интеграла. ∫∫_D C*f(x,y)ds = C* ∫∫_Df(x,y)ds

Свойство 2. Двойной интеграл, от алгебраической суммы двух функций равен алгебраической суммы двойных интегралов от этих функций.

∫∫_D[f₁(x,y)+f₂(x,y)]ds=∫∫_Df₁(x,y)ds+∫∫_Df₂(x,y)ds

Свойство 3. Если область интегрируемая D разбита на две части D₁ и D₂ не имеющих общих внутренних точек, то

∫∫_Df(x,y)ds=∫∫_D1f(x,y)ds+∫∫_D2f(x,y)ds

Свойство 4. Если всюду в области Df(x,y)≥0 то

∫∫_Df(x,y)ds≥0 f(x,y)≤0 ∫∫_Df(x,y)ds

Свойство 5. Если всюду в области D f(x,y)≥ꝕ(x,y) то

∫∫_Df(x,y)ds≥∫∫_Dꝕ(x,y)ds

Свойство 6. Если m и M – соответственно наименьшее и наибольшие значения функции f(x,y) в области D, то m*s<∫∫_Df(x,y)ds≤M*S, где S площадь области интегрирования.

Свойство 7. Если f - интегрируемая на D функция, то | f | - также интегрируемая, причем | ∫∫_Df(x,y)ds|≤ ∫∫_D|f(x,y)|ds.

Свойство 8. Теорема о среднем для двойного интеграла. Если функция f(x,y) непрерывна в замкнутой области D, то найдется такая точка M(x,y) что справедливо равенство: ∫∫_Df(x,y)ds=f(x,y)*s. s-площадь

Вычисление двойных интегралов в декартовой системе координат

Формула вычисления двойного интеграла

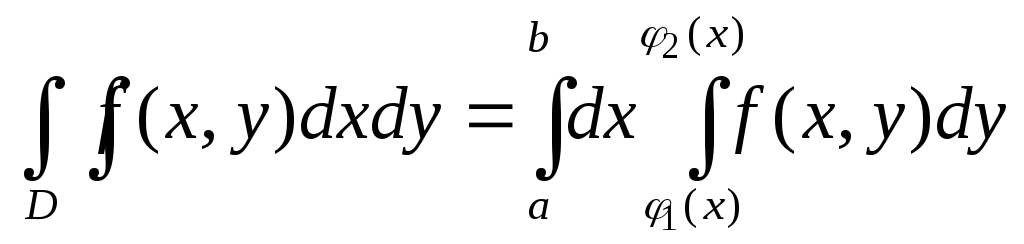
Правило вычисления двойного интеграла:

1. Строим область интегрирования и проверяем является ли она правильной и стандартной в направлении оси OY

2. Разрешаем уравнение границы

3. Переходим от двойного интеграла к повторному расставляя у повторного приделы интегрирования.

4. Берем внутренний интеграл по y при произвольном постоянном x.

5. Вычисляем внешний интеграл.

Вычисление двойного интеграла в полярной системе координат.

Преобразовав координаты x=x(u,v) y=y(u,v) приводят к двойному интегралу:

где I- якобиан

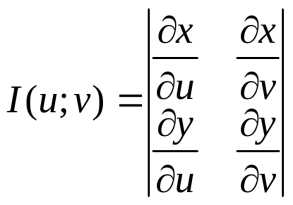
Не равен 0

Применение двойного интеграла.

1. Площадь плоской фигуры

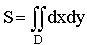
2. Масса плоской фигуры

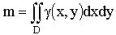
3. Статические моменты пластины относительно осей Ox и Oy:

4. Моменты инерции пластины относительно осей Ox, Oy и начала координат:

5. Тройной интеграл как предел интегральной суммы и его свойства.

Определение: Конечный предел интегральной суммы функции f(x,y,z) в области омега при условии что максимальный диаметр стремится к 0, и число разбиений(n) стремится к нулю – называется тройным интегралом этой функции по области омега

∫∫∫_Ωf(x,y,z)dv=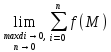

Свойство 1. Постоянный множитель можно вынести за знак двойного интеграла. ∫∫∫_D C*f(x,y)ds = C* ∫∫∫_Df(x,y)ds

Свойство 2. Двойной интеграл, от алгебраической суммы двух функций равен алгебраической суммы двойных интегралов от этих функций.

∫∫∫_D[f₁(x,y)+f₂(x,y)]ds=∫∫∫_Df₁(x,y)ds+∫∫_Df₂(x,y)ds

Свойство 3. Если область интегрируемая D разбита на две части D₁ и D₂ не имеющих общих внутренних точек, то

∫∫∫_Df(x,y)ds=∫∫∫_D1f(x,y)ds+∫∫∫_D2f(x,y)ds

Свойство 4. Если всюду в области Df(x,y)≥0 то

∫∫∫_Df(x,y)ds≥0 f(x,y)≤0 ∫∫∫_Df(x,y)ds

Свойство 5. Если всюду в области D f(x,y)≥ꝕ(x,y) то

∫∫∫_Df(x,y)ds≥∫∫∫_Dꝕ(x,y)ds

Свойство 6. Если m и M – соответственно наименьшее и наибольшие значения функции f(x,y) в области D, то m*s<∫∫∫_Df(x,y)ds≤M*S, где S площадь области интегрирования.

Свойство 7. Если f - интегрируемая на D функция, то | f | - также интегрируемая, причем | ∫∫∫_Df(x,y)ds|≤ ∫∫∫_D|f(x,y)|ds.

Свойство 8. Теорема о среднем для двойного интеграла. Если функция f(x,y) непрерывна в замкнутой области D, то найдется такая точка M(x,y) что справедливо равенство: ∫∫∫_Df(x,y)ds=f(x,y)*s. s-площадь

6.Вычисление тройного интеграла в декартовой системе координат.

В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.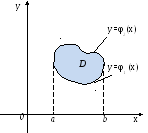

Если плоская область D ограничена линиями и() и прямымих=а и х=b (рис. 15), то тройной интеграл вычисляется по формуле

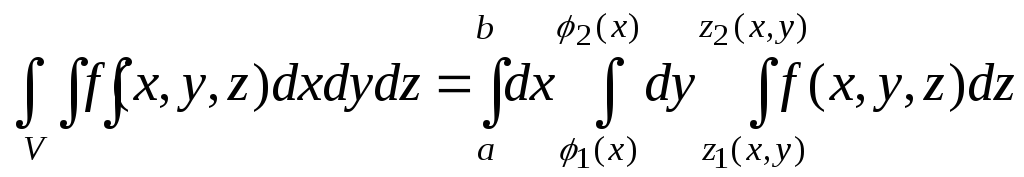
7.Цилиндрические координаты. Вычисление тройного интеграла в цск

Цилиндрическая система координат (ЦСК) определяется плоскостью , в которой задана полярная система координат и осью, перпендикулярной этой плоскости. Цилиндрическими координатами точкипространства называют тройку чисел, где– полярные координаты точки– проекции точкина плоскость, а– это координаты проекции точкина осьили.

В плоскости введем обычным образом декартовы координаты, ось аппликат направим по осиЦСК. Теперь нетрудно получить формулы, связывающие цилиндрические координаты с декартовыми:

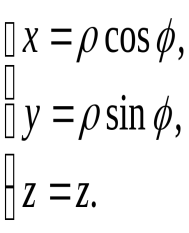
8.Сферическе координаты. Вычисление тройных интегралов в сск

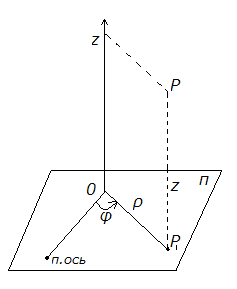
Сферическими координатами точки M(x,y,z) называются три числа − ρ,φ,θ, где  ρ − длина радиуса-вектора точки M; φ − угол, образованный проекцией радиуса-вектора −−→OM на плоскость Oxy и осью Ox; θ − угол отклонения радиуса-вектора −−→OM от положительного направления оси Oz (рисунок 1). Рис.1 Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга.  Сферические координаты точки связаны с ее декартовыми координатами соотношениями x=ρcosφsinθ, y=ρsinφsinθ, z=ρcosθ, гдеρ≥0,0≤φ≤2π,0≤θ≤π.

9.Применение тройных интегралов

1. Если некоторое тело ограничено областью G трехмерного пространства, то объем данного тела будет равен

2. Масса тела: 

3. Статические моменты тела относительно плоскостей Oxy, Oxz, Oyz:

4. Моменты инерции тела относительно плоскостей Oxy, Oxz, Oyz и начала координат:

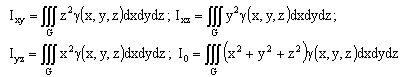
10.Криволинейный интеграл 1-го рада (по длине дуги)

Криволинейный интеграл по длине дуги от скалярных функций нескольких переменных есть число равное пределу интегральной функции этой суммы по данной дуге.

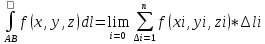
Теорема существования. Если функция f(x,y,z) непрерывна на кусочно-гладкой кривой , то она интегрируема по этой кривой.

Свойства: 1. Значение криволинейного интеграла по длине дуги не зависит от направления дуги кривой АВ.

2. Постоянный множитель можно выносить за знак криволинейного интеграла.

3. Криволинейный интерал от суммы функций равен сумме криволинейных интегралов от этих функций.

4. Если кривая АВ разбита на дуги АС и СВ, то

11.Вычисление Криволинейного интеграла 1-го рода

Случай	Формула для вычисления
1.Кривая задана параметрически x=x(t) y=y(t) z=z(t) t€(t1 t2)
2.Плоская кривая задана параметрически x=x(t) y=y(t) z=z(t) t€(t1 t2)
3.Плоская кривая заданна в явном виде y=y(t) x€(a,h)
Плоская кривая задана в полярных координатах