26.2. Уравнение Бернулли для элементарной струйки реальной жидкости

Благодаря вязкости в реальной жидкости происходят потери механической энергии потока на трение внутри жидкости и о стенки канала. При этом происходит рассеяние (диссипация) энергии. Энергия, потерянная на трение, превращается в теплоту и идет на пополнение запаса внутренней энергии жидкости, а часть ее отводится в виде тепла через стенки канала.

Внутренняя энергия жидкости не может быть непосредственно использована для приведения жидкости в движение и поэтому в гидравлике рассматривается как потеря механической энергии, т.е. потерю напора.

У реальной жидкости полная энергии не сохраняется,

,

Уравнение Бернулли принимает вид

, (26.2)

где h_1-2 – потеря напора на участке 1-2.

Для характеристики величины потерь на единице длины используется понятие гидравлического уклона

. (26.3)

Применение уравнения Бернулли для потока жидкости затрудняется неравномерностью распределения скоростей по живому сечению потока, наличием поперечных составляющих продольной скорости влиянием центробежных сил. Оно справедливо для установившихся плавноизменяющихся потоков, характеризующихся следующими особенностями:

1. Угол расхождения соседних струек, а следовательно, и поперечные составляющие скоростей в живых сечениях потока настолько малы, чтобы ими можно было пренебречь и рассматривать течение как плоское.

2. Кривизна линий тока настолько мала, а радиусы закруглений настолько велики, чтобы центробежными силами можно пренебречь.

3. Гидродинамическое давление в живых сечениях распределяется по законам гидростатики, т.е. сумма 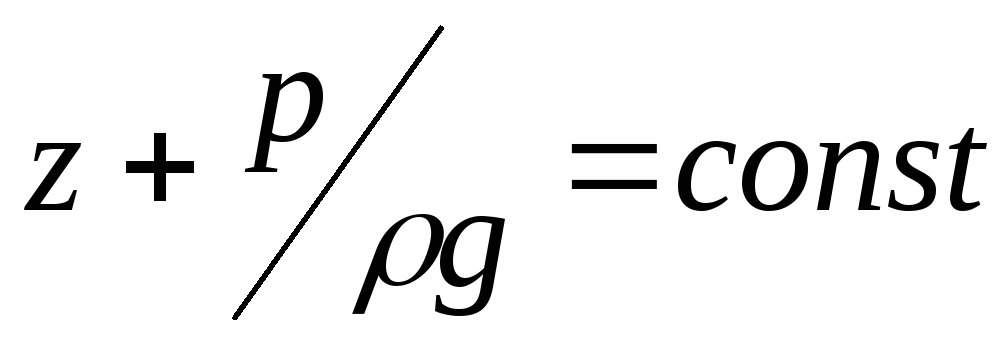для всех точек данного живого сечения.

В гидравлике расчеты обычно ведутся по средним скоростям. В этом случае уравнение Бернулли принимает вид

. (26.4)

Здесь  - коэффициент, зависящий от неравномерности распределения скорости по живому сечению потока. Дяля ламинарного течения  = 2, для турбулентного течения  = 1,05…1,1. Часто для упрощения расчетов принимают  = 1.

Лекция 27. Основы теории гидродинамического подобия

Для решения конкретных задач необходимо иметь количественные оценки протекающих процессов. Эти оценки могут быть получены двумя путями: аналитическим и экспериментальным. При аналитическом исследовании движения жидкости задача сводится к интегрированию уравнений Навье-Стокса при заданных начальных и граничных условиях и применительно к указанной конфигурации канала, в котором движется жидкость.

Однако подавляющее количество реальных задач могут быть подвергнуто аналитическому анализу только при существенном упрощении. Допустимость этих упрощений должна проверяться на опыте, а не основываться на удобстве математических преобразований. Для задач, не очень отличающихся от уже решенных, часто достаточно прежнего опыта. Но совсем новые задачи требуют новых опытов, т.к. неоправданные допущения могут провести к физически неверным заключениям.

При экспериментальном исследовании явлений возникают свои трудности. Во-первых, при разработке новых крупногабаритных устройств объект исследования отсутствует. Если создавать объект в полном масштабе, а затем на нем приводить исследования и по их результатам изменять конструкцию, то это приведет к огромным материальным и временным затратам. Для этой цели желательно испытывать меленькие дешевые модели и потом полученные результаты переносить на объект. В этом отношении справедливо пожелания Ф. Бэкона: «Делайте ошибки на малом, а пользу получайте на большом». Однако здесь возникает проблема: как конструировать модель, и каким образом переносить полученные результаты на натурный объект.

Во-вторых, при проведении экспериментов возникает проблема количества определяющих факторов и необходимого количества экспериментов. Если процесс зависит только от одного параметра, то для оценки одного состояния достаточно постановки одного опыта. Если процесс определяют два взаимосвязанных параметра, то для установления их взаимного влияния требуется, по крайней мер, четыре или пять опытов; при трех параметрах недостаточно двадцати опытов. С увеличением числа переменных трудность экспериментального исследования растет очень резко, и лишь немногие задачи движения жидкости могут быть сведены к трем, четырем или даже пяти подходящим переменным без чрезмерного упрощения.

В качестве примера можно рассмотреть достаточно простую задачу: определение гидравлического сопротивления трубы. Здесь на результат влияют, как минимум, шесть параметров: диаметр и шероховатость трубы, скорость течения, плотность и вязкость жидкости, перепад давления.

На данном этапе развития науки получение новых количественных данных о сложном объекте наиболее эффективно при сочетании теоретического и экспериментального методов. Теоретические основы для построения физических моделей реальных объектов, сокращения количества определяющих параметров и обобщения полученных результатов дает теория подобия.

Основная идея теории подобия состоит в том, что множественность параметров, существенных для исследуемого процесса, вовсе не является собственным свойством изучаемых задач, связанным с физической природой процесса. В действительности влияние отдельных параметров проявляется не порознь, а совместно, поэтому надо рассматривать не отдельные эти величины, а их совокупности, соединенные в комплексы строго определенного вида. Являясь вполне устойчивыми комбинациями из величин, существенных для изучаемых процессов, эти комплексы получают значение особого рода переменных, характерных для этих процессов.

Уравнения Навье-Стокса и уравнение неразрывности потока, описывающие движение вязкой жидкости, включают в себя большое количество разнородных величин (скорость, время, давление, линейные размеры, вязкость и плотность жидкости, ускорение свободного падения). Эти уравнения одновременно являются и очень сложными, и очень простыми. Они выражают очень простые идеи. Уравнение неразрывности является законом сохранения массы и отражает следующее положение: количество массы в выделенном объеме жидкости не меняется во время его движения. Уравнение Навье-Стокса выражает простое условие равновесия совокупности сил: в движущейся жидкости сила инерции, сила давления, сила тяжести и сила трения, действующие на выделенный элемент жидкости, уравновешивают друг друга.

Сложность уравнений появляется, когда силы, работа, потоки массы, давления записываются в простых переменных, т.е. в единицах массы, времени и протяженности.

Уравнения Навье-Стокса и уравнение неразрывности описывают все возможные виды движения вязкой жидкости в каналах любой формы. Решение системы относится ко всему классу явлений. Для получения однозначного решения, соответствующего конкретной задаче, должны быть указаны следующие параметры:

1. физические константы, отражающие свойства системы;

2. геометрические характеристики системы;

3. значения искомых параметров на границах системы (граничные условия);

4. значения параметров в начальный момент времени (начальные условия).

Формально каждый из параметров рассматривается как самостоятельная независимая переменная, получающая новое значение при изменении условий задачи. Но в действительности для процесса существенны не отдельные влияния, а суммарные воздействия. Отсюда следует, что и в условия задачи параметры можно вводить не как разрозненное множество индивидуальных величин, а в виде комплексов, в самой структуре отражено взаимодействие различных влияний.

Переход от обычных физических величин к величинам комплексного типа, составленных из тех же величин, но в определенных сочетаниях, создает важные преимущества. Прежде всего, уменьшается число переменных. Вместе с этим более четко проявляются внутренние связи, характеризующие процесс, и вся количественная картина становится более ясной. Очевидно, что заданное значение комплекса может быть получено как результат бесчисленного множества различных комбинаций составляющих его величин. Следовательно, полученное решение уже относится не к единичному случаю, а к целому классу явлений, для которых значения комплексов имеют одни и те же значения. Представление параметров задачи в виде комплексов дает возможность полученные на одном объекте результаты переносить на другие объекты, т.е. моделировать процессы, используя в качестве моделей объекты меньшего размера и позволяющие проводить более дешевые эксперименты. Условием подобия явлений в модели и объекте является равенство значений комплексов. Поэтому комплексы могут рассматриваться как критерии подобия.

Очевидно, что должно существовать определенное соответствие между структурой комплексов и структурой уравнений, описывающих процессы. Выражения, описывающие исследуемые эффекты, входят в уравнения в виде некоторых операторов, в частности, первых и вторых производных. Эти операторы связывают различные переменные. В отличие от них комплексы должны строиться из параметров, т.е. величин, которые для конкретной задачи являются постоянными и меняются только при переходе к другой задаче.

Допустим, что величины z₁ и z₂ задаются через величины x и y следующим образом

.

Из этих выражений видно, что величина z₁ прямо пропорциональна величине y и обратно пропорциональна величине х, а величина z₂ прямо пропорциональна величине y и обратно пропорциональна квадрату величины х. Поэтому величины z₁ и z₂ могут быть представлены в виде комплексов

.

Значения x₀ и y₀ не могут выбираться произвольно, они должны характеризовать конкретный процесс. Следует обратить внимание, что размерности и , и совпадают.

Уравнение Навье-Стокса для оси z модно записать в виде

.

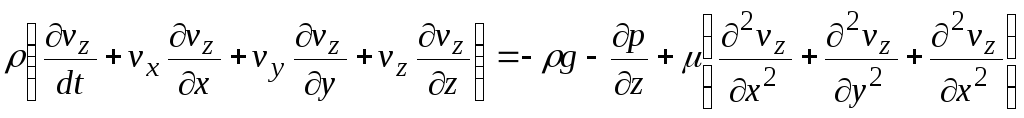Левая часть уравнения представляет собой силу инерции

.

Первый член в правой части уравнения есть сила тяжести

.

Второй член отражает действие силы давления

.

Третий член есть сила вязкого трения

.

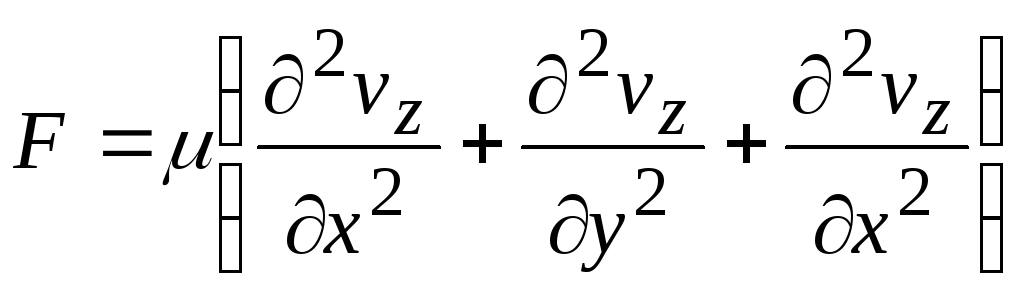Можно записать

. (27.1)

Ускорение элемента жидкости включает составляющую, связанную с нестационарностью процесса и представляемую выражением , а также конвективную составляющую, связанную с изменением скорости вследствие перемещения частицы в другую точку пространства и определяемую выражением . Мерой оценки влияния нестационарности на процесс движения жидкости будет отношение, выраженное в виде комплекса:

.

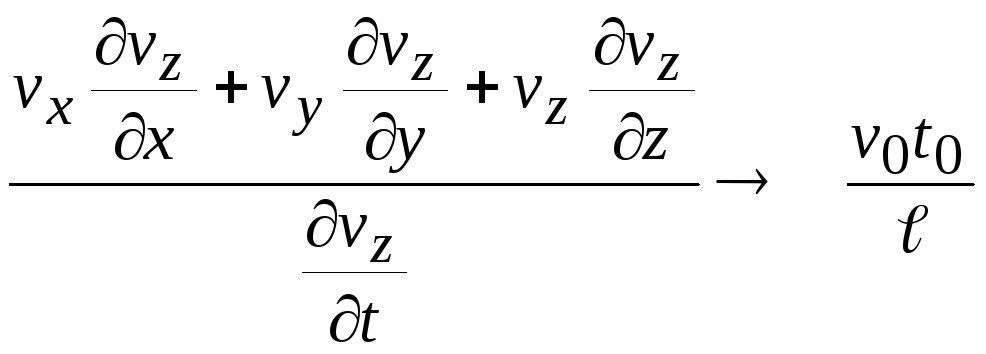Комплекс

(27.2)

называется критерием гомохронности. Величина v₀ соответствует скорости, характерной для данного процесса; ℓ - характерный размер канала; t₀ - характерное время процесса.

Для стационарных режимов составляющая отсутствует. Отношение силы инерции к силе вязкого трения дает комплекс

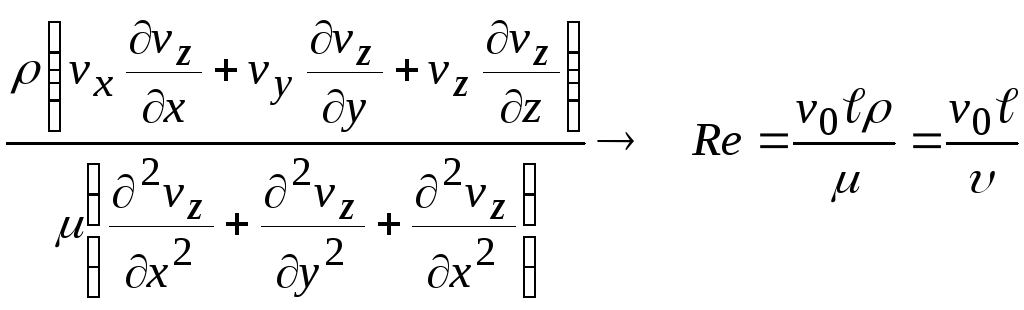. (27.3)

Этот комплекс называется критерием Рейнольдса.

Отношение силы инерции к силе тяжести дает комплекс, называемый критерием Фруда.

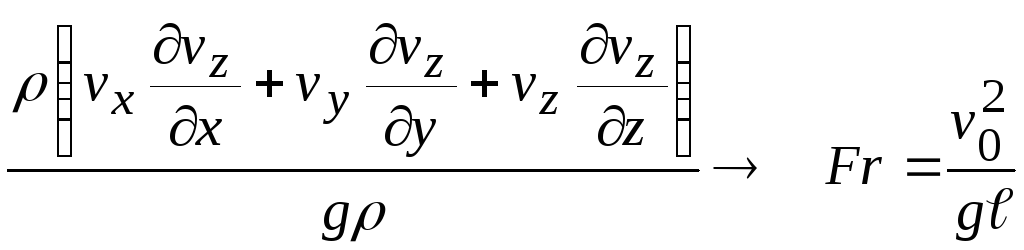(27.4)

Отношение силы давления к силе инерции дает комплекс, называемый критерием Эйлера

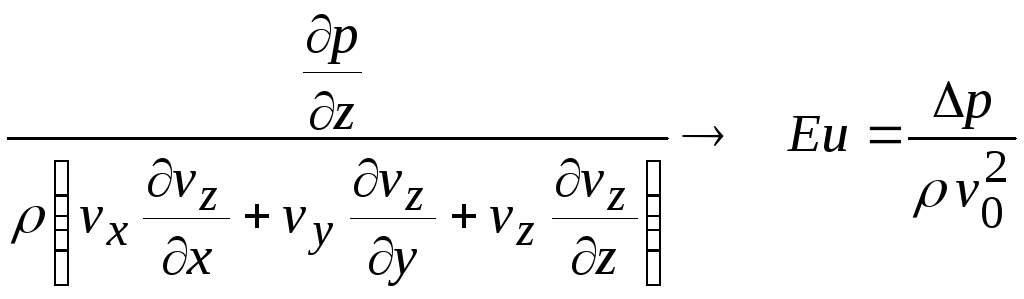(27.5)

Для течения несжимаемой жидкости существенным является не давление р, а перепад давления р. Вследствие того, что заданному полю скорости соответствует единственно возможное распределение сил давления, значение критерия Эйлера для конкретной задачи является функцией остальных критериев и безразмерных параметров

. (27.6)

По этой причине комплекс часто называют не критерием, а числом Эйлера.

Основные положения теории подобия обобщаются теоремами подобия. Эти теоремы лежат в основе практического применения теории подобия.

Первая теорема подобия (Ньютона): Подобные явления характеризуются численно равными критериями подобия.

Вторая теорема подобия (Бэкингема, Федермана): Решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде зависимости между безразмерными комплексами этих величин, т.е. между критериями подобия.

Третья теорема подобия (Кирпичева, Гухмана): Подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и у которых соблюдается подобие условий однозначности.