Ламинарное течение жидкости

Главным свойством ламинарного течения является его слоистая структура без перемешивания частиц. Поток движется только в направлении, параллельном оси трубы при полном отсутствии поперечных движений жидкости.

Из-за вязкости жидкость прилипает к стенке, поэтому скорость слоя, непосредственно контактирующая со стенкой, равна нулю. По мере удаления от стенки скорость возрастает и на оси трубы достигает максимального значения.

Рассмотрим установившееся движение жидкости в круглой горизонтальной трубе. Движение происходит под действием перепада давления в направлении оси трубы. В поперечном сечении, перпендикулярном оси трубы, давление постоянно. Вследствие трения от одного цилиндрического слоя к другому передается касательное напряжение, пропорциональное градиенту скорости . Следовательно, движение каждого элемента жидкости ускоряется вследствие перепада давления и тормозится вследствие напряжения сдвига, вызванного трением. Другие силы на жидкость не действуют.

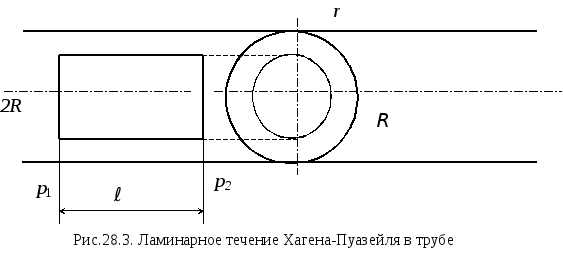
Мысленно вырежем из жидкости, содержащейся в трубе, цилиндр длиною ℓ, радиусом r и осью, совпадающей с осью трубы (рис.28.3).

В направлении оси цилиндра на левое основание цилиндра действует сила давления , на правое основание – сила давления , на боковую поверхность цилиндра действует касательная сила . Силы давления и сила трения уравновешивают друг друга. Приравнивая их, получим

. (28.1)

Так как максимум скорости достигается на оси трубы, а приближении к стенке трубы скорость снижается до нуля, то величина касательного напряжения будет равна

. (28.2)

Из (28.1) и (28.2) следует

. (28.3)

Интегрируя (28.3), получим

. (28.4)

Постоянную интегрирования определим из условия прилипания жидкости к стенкам трубы: . Отсюда . Формула (28.4) принимает вид

. (28.5)

Из (28.5) следует, что при ламинарном течении в трубе профиль скорости соответствует параболе. На оси трубы скорость максимальна и равна

. (28.6)

Расход жидкости через кольцевой зазор, ограниченный радиусами , равен

, (28.7)

Суммарный расход через трубу

. (28.8)

Средняя скорость движения жидкости

. (28.9)

Из (28.6) и (28.9) следует, что при ламинарном течении скорость на оси трубы вдвое больше средней скорости жидкости в трубе. При этом скорость потока и расход жидкости прямо пропорционален перепаду давления .

Формула (28.8) впервые была выведена Хагеном и затем независимо от него Пуазейлем.

Формула (28.8) используется для определения вязкости жидкости. Берется капилляр определенного диаметра и для заданной длины капилляра определяется перепад давления и расход, а затем по (28.8) вычисляется .

Лекция 29. Турбулентное течение жидкости

При увеличении скорости потока выше критической начинается потеря устойчивости ламинарного течения. В потоке образуются вихри, появляются пульсации скорости и давления. Вовлеченные в вихри элементы жидкости перемещаются вдоль и поперек потока и представляют собой не отдельные молекулы, а более или менее крупные образования, турбулентные моли или глобулы. Вихри возникают, некоторое время существуют в виде индивидуальных элементов и распадаются. Объемы вовлеченной массы и время существования вихрей являются случайными величинами.

Обычно представляют турбулентное движение в виде осредненного движения, скорость которого в среднем за некоторый период времени Т остается постоянной, и наложенного на него пульсационного движения, средняя скорость которого за тот же период времени равна нулю. Для проекций скорости и давления имеем:

(29.1)

. (29.2)

Уравнение неразрывности, записанное для полной скорости, имеет вид

, (29.3)

откуда

, (29.4)

. (29.5)

Из (29.4) и (29. 5) следует, что уравнение неразрывности справедливо как для средних, так и для пульсационных составляющих скоростей потока.

Основная идея подхода к описанию турбулентных течений, предложенная Рейнольдсом, состоит в допущении, что действительное движение, включающее осредненные и пульсационные составляющие, строго описывается уравнениями Навье-Стокса. Записывая уравнение Навье-Стокса для турбулентного движения несжимаемой жидкости и проводя осреднение, получим

(29.6)

Система (29.6) называется уравнениями Рейнольдса. В отличие от уравнений Навье-Стокса для ламинарного потока в правой части уравнений Рейнольдса появился третий член, содержащий произведение пульсационных составляющих скоростей. Принципиальным для турбулентного течения является то, что пульсационное движение со скоростями влияет на осредненное движение таким образом, что в осредненном движении как бы увеличивается сопротивление возникновению деформаций, т.е. возникает дополнительная вязкость среды.

Система уравнений Рейнольдса является незамкнутой, так как количество неизвестных превышает количество уравнений. Для ее замыкания необходимо ввести дополнительные уравнения, связывающие компоненты турбулентного напряжения с осредненными составляющими скоростей.

В основе расчета турбулентных полей скоростей, температуры и концентрации примесей лежат эмпирические гипотезы, связывающие силы кажущейся вязкости, вызываемой турбулентным перемешиванием, с осредненными во времени скоростями, а также соответствующие эмпирические гипотезы для тепло- и массообмена.

В 1877 г. Ж. Буссинеском была предложена гипотеза о связи величины касательных напряжений с осредненной скоростью. Согласно закону трения Ньютона при ламинарном течении касательные напряжения определяются выражением :

.

Коэффициент молекулярной динамической вязкости  зависит от природы жидкости, т.е. представляет собой физическую характеристику жидкости. Буссинеск предположил, что турбулентное кажущееся касательное напряжение _t определяется аналогичной формулой:

, (29.7)

в которой вместо истинной скорости v_x входит осредненная скорость , а вместо коэффициента молекулярной вязкости  - коэффициент турбулентного обмена или коэффициент турбулентной вязкости _t.

Здесь надо иметь в виду, что величина _t зависит от распределения скорости и, следовательно, не является, подобно коэффициенту молекулярной вязкости , физической константой.

При ламинарном течении сила трения прямо пропорциональна скорости, а следовательно, и производной скорости . Поэтому величина  не может зависеть от величины скорости. При турбулентном течении сила трения пропорциональна квадрату скорости, поэтому коэффициент турбулентной вязкости _t должен быть пропорционален первой степени скорости.

Вместо коэффициента динамической турбулентной вязкости _t часто используется коэффициент кинематической турбулентной вязкости _t, соответствующий коэффициенту кинематической молекулярной вязкости  и определяющийся по формуле:

. (29.8)

Сумма коэффициентов молекулярной и турбулентной вязкостей называют эффективной вязкостью.

Уравнение Рейнольдса для вязкой несжимаемой жидкости принимает вид:

(29.9)

Следует обратить внимание на то, что в правой части уравнений величину _е нельзя вынести за знак производной, т.к. турбулентная составляющая _t зависит от координаты точки.

Чтобы использовать формулу Буссинеска (29.7), необходимо найти подходящие гипотезы о связи между коэффициентом турбулентной вязкости _t и полем осредненных скоростей. В этом направлении плодотворным оказался подход, предложенный Л. Прандтлем в 1925 г.

Рассмотрим плоское течение с направлением, одинаковым во всех точках пространства, и со скоростью, изменяющейся только при переходе от одной линии тока к другой. Координатные оси выберем таким образом, чтобы направление основного течения совпадало с осью х и было перпендикулярно оси у. Это течение схематично показано на рис. 29.1.

Из касательных составляющих тензора напряжений в рассматриваемом случае имеется только касательное напряжение

.

Механизм турбулентного течения можно представить следующим образом. В турбулентном потоке возникают жидкие объемы, каждый из которых обладает собственной скоростью и движется на протяжении некоторого расстояния как в продольном, так и поперечном направлении в виде неразрывного целого с сохранением х-составляющей своего импульса.

Предположим, что один такой жидкий объем, возникший в слое (у₁-) и обладающий скоростью , перемещается на расстояние  в направлении у, перпендикулярном к основному течению. Расстояние  называется путем перемешивания. Если рассматриваемый объем сохраняет х-составляющую своего импульса, то в новом слое он будет иметь меньшую разность, чем окружающая его новая среда. Разность между новой и старой скоростями будет равна

.

При таком поперечном течении .

Аналогичным образом жидкий объем, попадающий в слой у₁ из слоя (у₁+), имеет в новом месте скорость выше, чем окружающая его среда. Разность скоростей составит

,

при этом .

Каждую из скоростей и , вызванных поперечным движением, можно понимать как турбулентную пульсацию скорости в слое у₁. Осредненное во времени значение абсолютной величины этой пульсации будет равно

. (29.10)

Это соотношение позволяет дать пути перемешивания  следующее физическое толкование. Путь перемешивания представляет собой то расстояние в поперечном направлении течения, которое частица жидкости, двигаясь со средней скоростью своего первоначального слоя, должна пройти для того, чтобы разность ее скорости и скорости течения в новом месте стала равной осредненному значению абсолютной величины продольной пульсации турбулентного течения.

Возникновение пульсаций скорости в поперечном направлении можно представить следующим образом.

Два жидких объема, один из слоя (у₁-), а другой из слоя (у₁+), попадают в слой у₁ и располагаются в нем один за другим так, что более быстрый объем из слоя (у₁+) оказывается позади более медленного объема из слоя (у₁-). В этом случае оба объема сталкиваются со скоростью и получают при этом боковое отклонение, в результате чего возникает поперечное движение, направленное в обе стороны от слоя у₁. Если же впереди оказывается более быстрый объем, то они удаляются друг от друга со скоростью . В этом случае образующееся между обоими объемами промежуточное пространство заполняется окружающей жидкостью, вследствие чего возникает поперечное движение, направленное с обеих сторон к слою у₁. Отсюда следует, что величина поперечной скорости имеет такой же порядок, что и величина продольной скорости . Можно записать

, (29.11)

где ₁ – коэффициент пропорциональности.

Частицы жидкости, приходящие в слой у₁ с положительным значением (на рис.29.1 – снизу вверх), вызывают преимущественно отрицательную пульсацию , поэтому для таких частиц произведение отрицательно. Частицы жидкости, приходящие в слой у₁ с отрицательным значением (на рис.29.1 – сверху вниз), вызывают преимущественно положительную пульсацию , поэтому для таких частиц произведение также отрицательно. Таким образом, осредненное во времени значение отличается от нуля, и при том отрицательно. Поэтому можно принять, что

, (29.12)

где коэффициент k всегда больше нуля, но меньше единицы. Здесь надо отметить, что осреднение по времени проводится не для пульсационных скоростей и , которые могут быть положительными и отрицательными, а их средние значения по определению равны нулю. Осреднение производится для их абсолютных значений и , которые всегда больше нуля.

Подставляя (29.10) и (29.11) в (29.12), получим

.

Заменяя три численных коэффициента одним , окончательно будем иметь

. (29.13)

Коэффициент также называется длиной пути перемешивания.

Величина турбулентного касательного напряжения будет равна

. (29.14)

Сопоставляя (29.14) с формулой Буссинеска (29.7), получим выражение для оценки коэффициента динамической турбулентной вязкости

. (29.15)

Соответственно коэффициент кинематической турбулентной вязкости будет равен

. (29.16)

Для расчета турбулентных течений надо знать значение пути перемешивания . При турбулентном течении сопротивление пропорционально квадрату скорости. Согласно (29.15) в этом случае величина не должна зависеть от абсолютного значения скорости. Однако эта величина не является физической константой, а определяется характеристиками потока.

Рассмотрим установившееся турбулентное течение жидкости в круглой трубе. Предположим, что касательные напряжения по всему поперечному сечению трубы одинаковы и равны касательному напряжению на стенке трубы ₀, а длина пути перемешивания пропорциональна расстоянию от стенки у:

,

где k – коэффициент пропорциональности. Тогда, исходя из (6.21), получим

,

оттуда

. (29.17)

Величина

(29.18)

имеет размерность скорости и называется динамической скоростью. Она является важной характеристикой турбулентного течения, но представляет собой только расчетную величину и не имеет физического смысла.

Интегрируя (29.17) с учетом (29.18), получим

, (29.19)

где С – постоянная интегрирования.

Из (29.19) следует, что при турбулентном течении в круглой трубе профиль скорости изменяется по логарифмической зависимости.

Выражение (29.19) действительно только для турбулентного течения и не описывает распределение скорости вблизи у стенки. Постоянную интегрирования С найдем из условия, что на оси трубы при y = r₀ скорость максимальна и равна v_max. Получим

. (29.20)

Для гладких труб можно принять k = 0,4. Тогда (29.20) принимает вид

. (29.21)

Тщательные измерения показали, что вблизи центра трубы распределение скоростей несколько отличается от логарифмического, но это отличие несущественно, поэтому в практических расчетах его можно не учитывать. На основании этого считают, что логарифмический профиль скоростей является пригодным для широкого диапазона чисел Re.

Универсальность логарифмического профиля объясняется прежде всего тем, что в формулу (29.21) входит динамическая скорость u_*, определяемая через трение на стенке, которое, в свою очередь, зависит от числа Re. Отсутствие данных о величине трения на стенке делает затруднительным применение этого распределения.

Более простым, но менее универсальным профилем скоростей при турбулентном движении является степенной профиль в виде

, (29.22)

где показатель степени n зависит от числа Re и с увеличением его убывает. Для течения при .

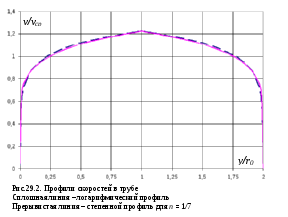
На рис.29.2 приведены профили скоростей, рассчитанные по (29.22) и (29.21) для . Из рисунка видно, что профили практически совпадают.