Кинематика точки в криволинейных координатах

В общем случае всякие три числа, однозначно определяющие положение точки в пространстве могут рассматриваться как координаты этой точки. Установив закон выбора этих чисел для любой точки, мы тем самым выбираем определенную систему координат, которая может иметь оси, направленные не только по прямым, но и по определенным кривым.

Обозначим через q₁, q₂, q₃ общие координаты точки, связанные некоторым образом с декартовыми координатами x, y, z. Положение точки М наряду с тройкой чисел x, y, z может быть также задано тройкой чисел q₁, q₂, q₃. Радиус-вектор точки М можно рассматривать как вектор-функцию координат .

Зафиксируем значения координат q₂= q₂₀, q₃=q₃₀ и будем изменять только координату q₁. Кривая, которую вычертит точка М, называется координатной линией (q₁).Через каждую точку М₀ можно провести три координатные линии:

линия (q₁): ,

линия (q₂): ,

линия (q₃): .

Касательные к координатным линии в точке М₀ называются координатными осями [q₁], [q₂], [q₃] в данной точке. Направление этих осей задается единичными векторами .

Если зафиксировать только одну координату и изменять сразу две координаты, то получим координатные поверхности:

поверхность (q₁, q₂): ,

поверхность (q₂, q₃): ,

поверхность (q₃, q₁): .

Касательные плоскости к координатным поверхностям называются координатными плоскостями. Координатные линии (q₁) и (q₂) лежат на координатной поверхности (q₁,q₂), линии (q₂) и (q₃) – на поверхности (q₂,q₃), линии (q₁) и (q₃) – на поверхности (q₁,q₃).

В декартовой прямоугольной системе координатные линии совпадают с координатными осями, а координатные поверхности совпадают с координатными плоскостями.

Д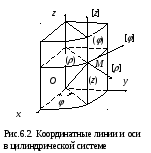ля описания движения жидкости в цилиндрических каналах более удобными являются цилиндрические координаты, в которых, как показано на рис.6.2, положение материальной точки задается проекцией  радиус-вектора на плоскость Оху, углом  между осью Ох и проекцией  и расстоянием точки от плоскости Оху.

Изменяя только одну координату , получим прямую, пересекающую ось Oz под прямым углом на высоте z и образующую с плоскостью Оxz угол . Эта прямая является одновременно координатной линией () и координатной осью []. Изменяя координату , получим окружность радиуса , лежащую в плоскости, перпендикулярной к оси Oz и находящейся на расстоянии z от плоскости Oxy. Эта окружность является координатной линией (), касательная к ней в точке М в сторону возрастания угла  - координатной осью []. Прямая, проходящая через точку М параллельно оси z, является одновременно координатной линией (z) и координатной осью [z].

Координатная поверхность (), соответствующая заданному значению z, представляет собой плоскость, перпендикулярную оси Oz. Координатную поверхность (z), соответствующую заданному значению , образует цилиндрическая поверхность радиуса  с осью Oz. Координатную поверхность (z) образует плоскость, проходящая через ось Oz и точку М. Эта плоскость образует с осью Ox угол .

Разложение радиус-вектора по единичным векторам имеет вид

. (6.7)

Проекциями радиус-вектора на координатные оси x, y, z являются величины  cos ,  sin  и z.

Рассмотрим производную . Частная производная по q₁ определяется при условии, что рассматриваются только изменения положения радиус-вектора по направлению координатной линии (q₁) и направление производной совпадает с направлением координатной оси [q₁], задаваемым единичным вектором . Тогда имеем

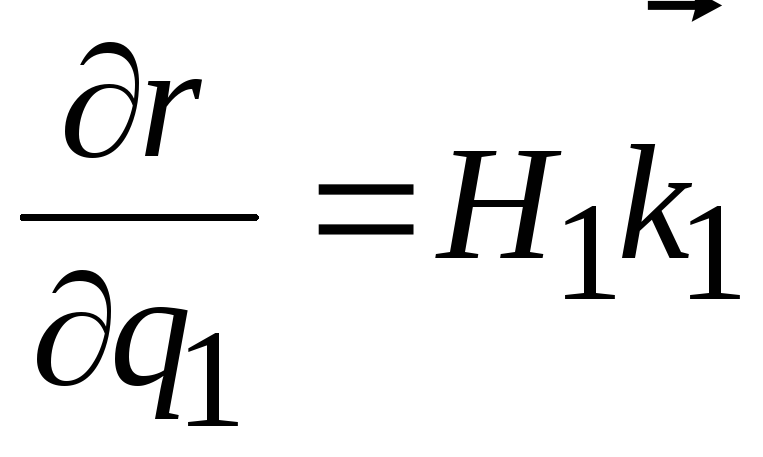, (6.8)

где Н₁ – длина вектора .

С другой стороны согласно (4.1)

. (6.9)

Из (4.8) и (4.9) следует, что скалярное произведение вектора на самого себя

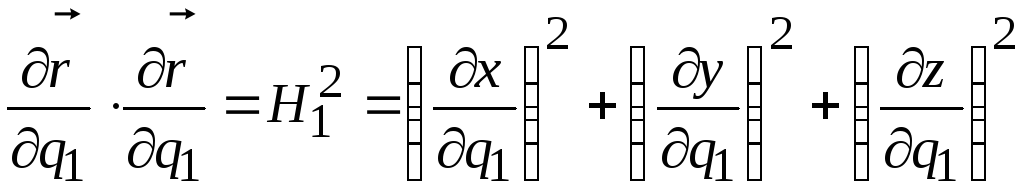, (6.10)

откуда

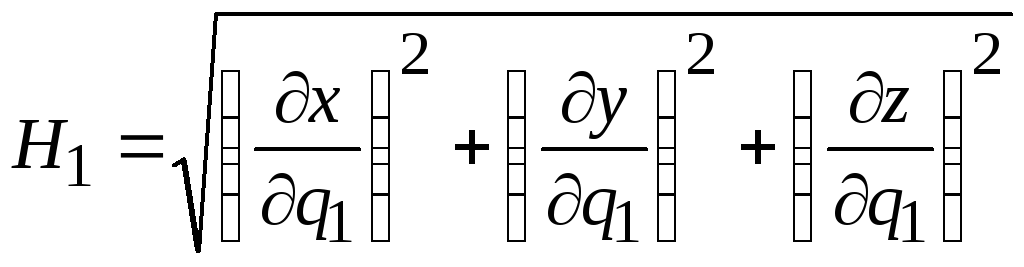. (6.11)

Проводя аналогичные рассуждения, получим

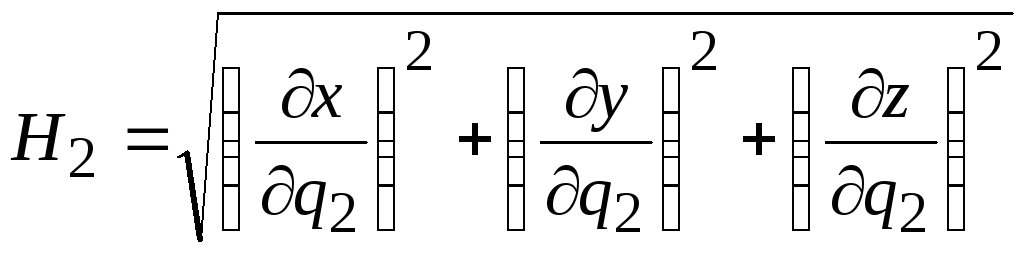, (6.12)

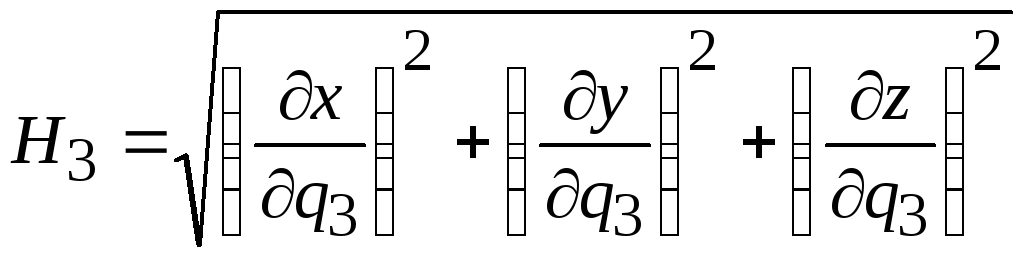. (6.13)

Коэффициенты H_i называются коэффициентами Ламе.

Наиболее существенное отличие криволинейных координат от декартовых состоит в том, что в криволинейной системе направления единичных векторов зависят от положения точки М в пространстве. Наиболее часто используются криволинейные ортогональные координаты, в которых вектора взаимно перпендикулярны. В частности, цилиндрические и сферические координаты являются ортогональными.

Необходимым и достаточным условием ортогональности криволинейных координат является равенство нулю скалярного произведения векторов, параллельным разнонаправленным координатным осям:

(6.14)

или

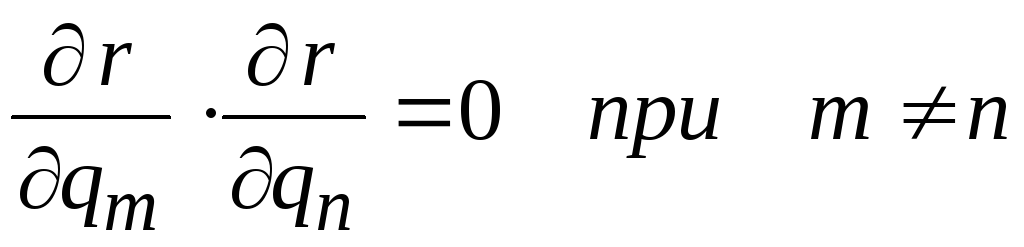. (6.15)

С учетом (4.9) и (4.15) условие ортогональности можно записать в виде

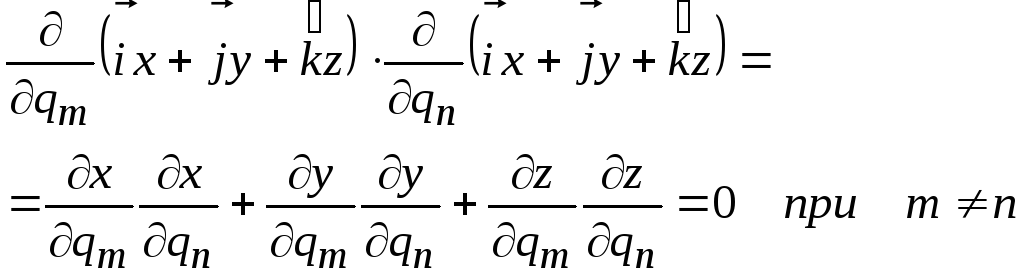. (6.16)

В дальнейшем будем рассматривать только ортогональные системы координат.

Разложим бесконечно малое изменение положения радиус-вектора по координатным осям.

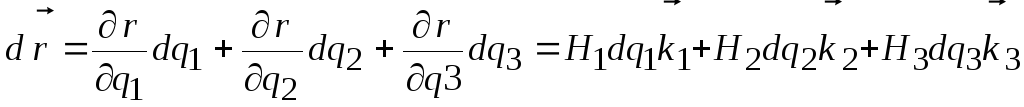. (6.17)

Абсолютное значение этого изменения есть длина дуги, описываемая точкой М. Изменения положения точки по координатным осям составят

. (6.18)

В цилиндрических координатах

.

Отсюда следует, что

. (6.19)

Скорость точки есть производная радиус-вектора по времени. Из (6.17) имеем

. (6.20)

В цилиндрических координатах проекции скорости на координатные оси равны:

радиальная скорость, направленная по радиусу от центра координат

, (6.21)

тангенциальная (окружная) скорость, перпендикулярная радиальной и находящаяся в плоскости ()

, (6.22)

осевая скорость, перпендикулярная плоскости ()

. (6.23)

В цилиндрических координатах полная скорость точки есть векторная сумма проекций скорости на координатные оси

. (6.24)

Ускорение точки есть скорость изменения ее скорости или вторая производная радиус-вектора по времени. Возьмем производную по времени от (6.24). Получим

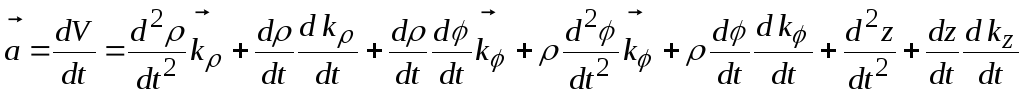. (6.25).

Рассмотрим производные единичных векторов осей по времени. Вектор перпендикулярен вектору и совпадает по направлению с вектором , а по абсолютной величине равен , т.е.

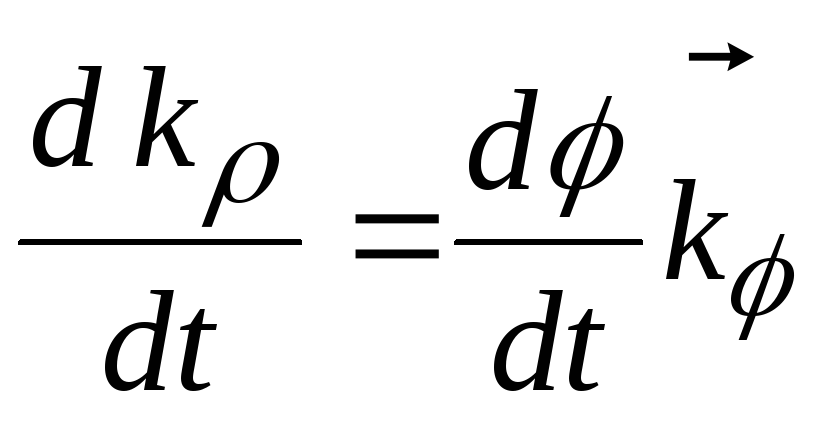. (6.26)

Вектор перпендикулярен вектору и направлен противоположно вектору , а по абсолютной величине равен . Отсюда

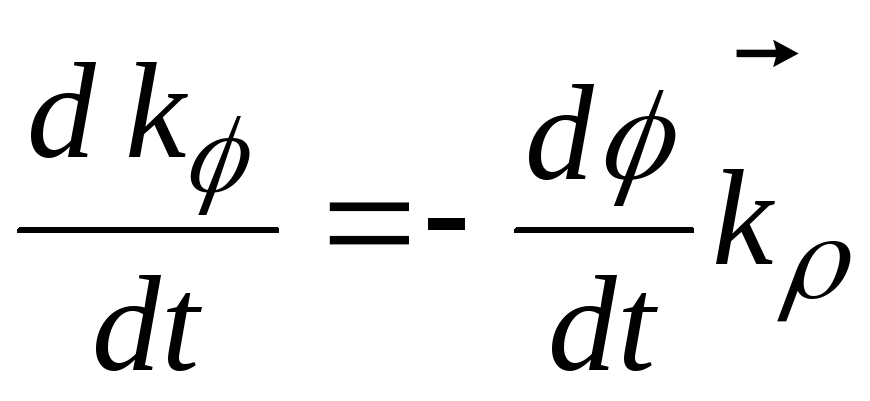. (6.27)

Так как направление оси z по времени не меняется, то

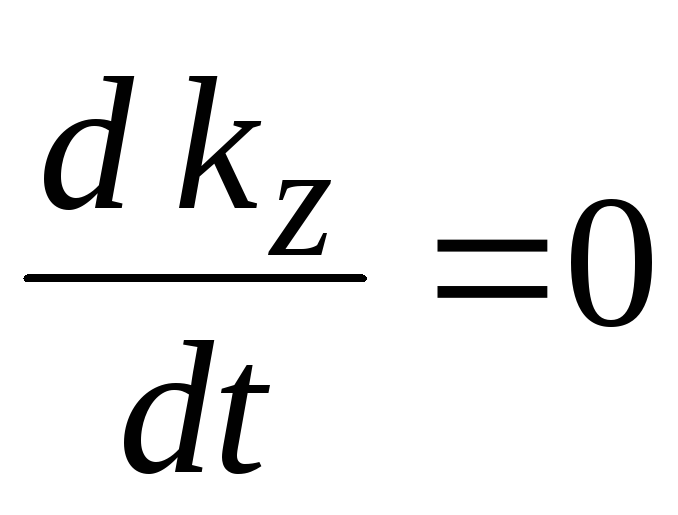. (6.28)

Подставляя (4.26) – (4.28) в (4.25), получим

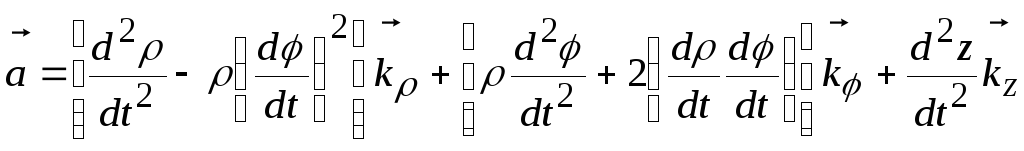. (6.29)

Составляющая ускорения, направленная по радиусу (радиальное ускорение)

. (6.30)

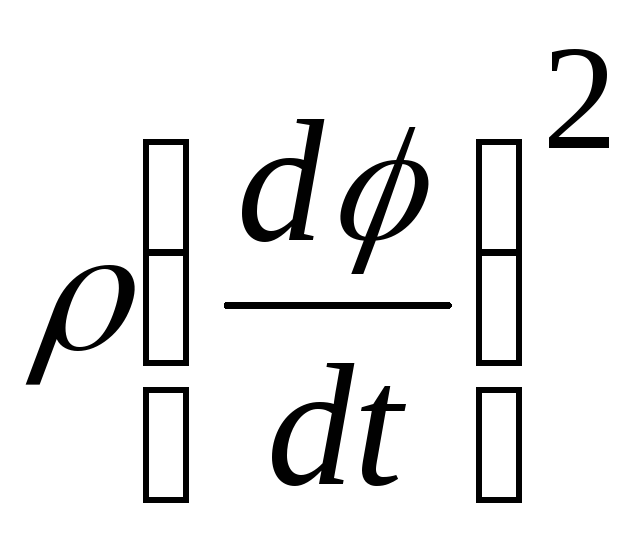При этом член есть ускорение частицы, вызванное движением ее в радиальном направлении, а величина представляет собой центростремительное ускорение, обусловленное вращением радиус-вектора.

Составляющая ускорения, перпендикулярная радиус-вектору и направленная в сторону его вращения (тангенциальное ускорение)

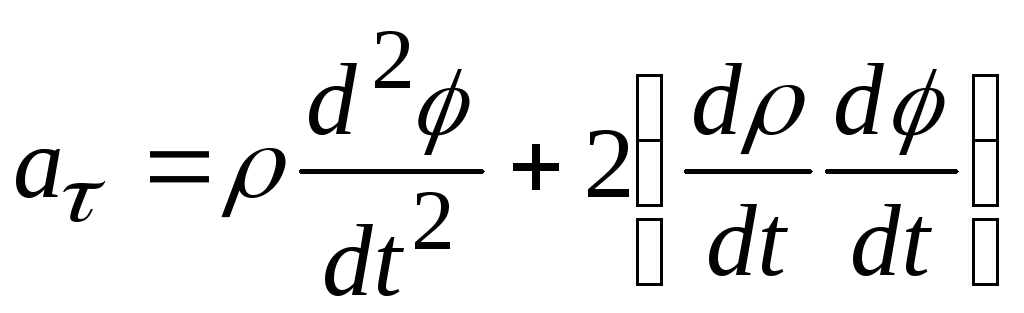. (6.31)

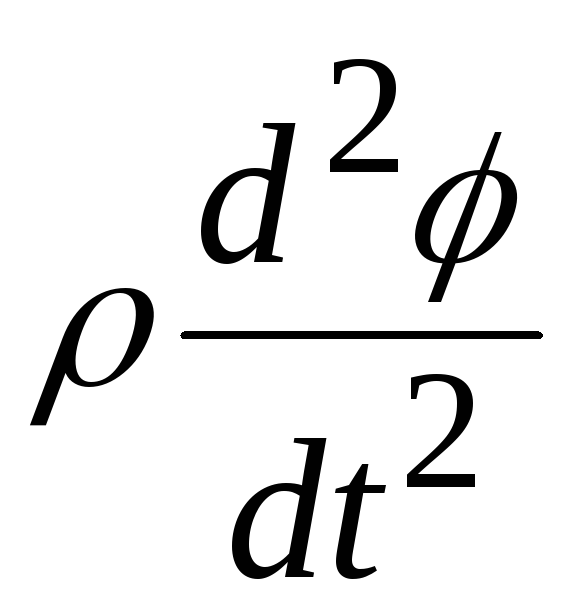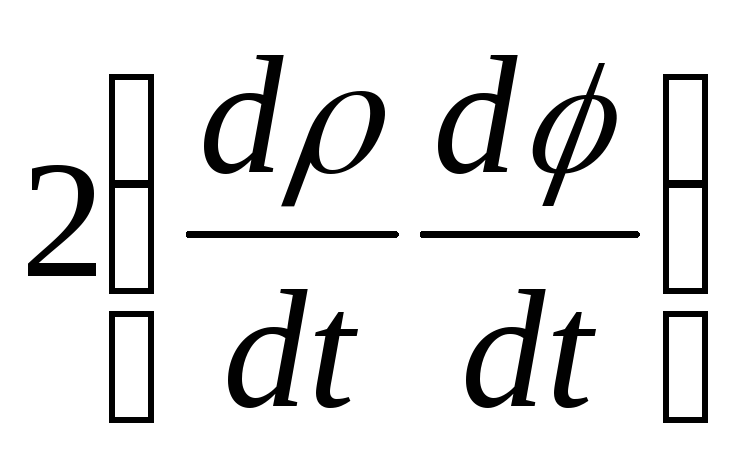Величина обусловлена изменением скорости вращения радиус-вектора, а величина представляет собой поворотное или кориолисово ускорение.

Составляющая ускорения, перпендикулярная радиальной и тангенциальной составляющей, и направленная вдоль оси z (осевое ускорение)

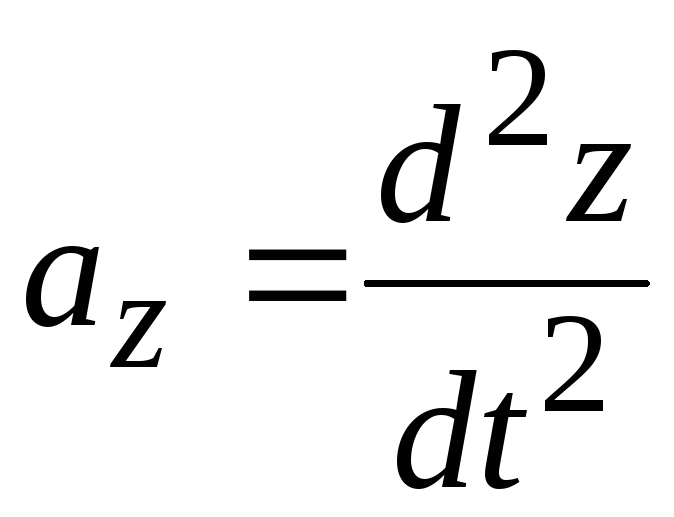. (6.32)

Величина полного ускорения

. (6.33)