расчетные методы дозиметрии бета-излучения

θ очень близки по форме и различаются в основном лишь масштабами по оси толщин X.

Это свойство функции f можно представить в виде равенства: Ƒ(x, Ei, θ)≈Ψ(z, θ) (5)

где Z=x/R ( Ei)− относительная глубина, измеренная в долях среднего пробега R электронов с энергией Ei.

Соотношение (5) выражает приближение “универсальных” или “единых дозовых функций”, использованное при решении некоторых задач дозиметрии электронов и бета−излучения. Универсальность формы дозных распределений fбылаэкспериментальноустановленавработеГ.Б.РадзиевскогоиД.П.Осанова/15/длясравнительноузкогодиапазонаEiидляугловпаденияθ≤600.Последующие измерения, проведенные авторами работы /15/, показали, что область применимостиприближения(5)сточностьюнехуже±20%можетбытьрасширена по крайней мере вплоть до θ=750 и Ei= 50кэв.

На возможность существования универсальности в форме как токовых распределений (кривых трансмиссий), так и расчётных дозных распределений для геометрии а) в широком диапазоне энергии, обратили внимание давно. Это свойство распределений иногда упоминается в литературе в качестве т.н. “закона преобразования масштаба” (scaling low). “Закон преобразования масштаба”(безотносительно к геометрии источника) можно обосновать теоретически, правда, в очень грубом приближении, если принять, что замедление электронов происходит непрерывно, а начальная энергия их Ei значительно меньше 2mc2=1,02 Мэв. Поскольку указанное обоснование не является корректным доказательством универсальности формы истинных распределений, последнее может быть получено из анализа результатов детальных расчётов или измеренийтоковыхидозныхраспределенийдляконкретныхгеометрическихусловий распространения излучения. В качестве такого доказательства для геометрии а) можно рассматривать, в частности, расчётные результаты /11/, полученные

вшироком диапазоне энергии. По данным этой работы дозные распределения в легкоатомных материалах универсальны по форме с 20%−точностью в интервале энергии, по крайней мере, от 25 кэв ( для меньшей энергии расчёты не производились) и до 2÷3 Мэв. Впрочем, истинные распределения для легкоатомных материалов, как было показано выше, заметно отличаются от вычисленных с использованием модели непрерывного замедления, ввиду чего

вданном случае, по−видимому, следует отдать предпочтение экспериментальным доказательствам.

Рассмотрим случай / / когда на плоской поверхности полубесконечного образца находится бесконечно широкий тонкий изотропный источник электро-

нов с энергией Ei. Считая, что с единицы площади источника эмитируется 1 электрон в единицу времени, мы запишем создаваемое этим источником одномерное дозное распределение (Х− глубина под поверхностью) в виде:

æ (x, Ei)=

tg

50

Сигнальный экземпляр

Что с учётом (4) и (5) перепишется как:

æ (x, Ei)≈ Ι (Ei)Ι[1+Δ(Ei)] ( , θ)tgθdθ

Ввиду слабой зависимости множителя /I+Δ(Ei, θ)/ от угла падения θ для легкоатомных материалов, соответствующее среднее значение вынесено в (7) из под интеграла. Для определения њ (Х, Е) необходимо в соответствии с (7), рас-

считать интеграл:

= F(z)

( , θ)tg θdθ

Вычисление функции F(z) было проведено путём численного интегрирования, причём в качестве f (z, θ) был взят набор глубинных доз распределений, полученный на основе измерений с мононаправленными электронными пучками, аналогичных измерениям описанным в /15/. Интеграл (8) при всех z>0 получается конечным из−за быстрого убывания функции f (z, θ) при θ→π/2 и при z>0. Как видно из (8), функция F (z) универсальна по крайней мере не в меньшей степени, чем подинтегральная функция f. График функции F (z) приведёнв//(рис.)и//(рис.).Вдиапазонеzот0,1до0,4F(z)удовлетворительно аппроксимируетсяпрямой2,06−3,08z,апри0,7≤z≤0,95−экспонентой405е-11z.

3.2.2. Иная форма «универсальности» глубинных дозных распределений

Сравнивая между собой дозные распределения в близких легкоатомных пластмассахотмононаправленныхэлектронныхпучковразнойэнергии,можно убедиться в том, что “универсальность” глубинных дозных распределений,

соответствующих одним и тем же	и разным Ei, можно представить и в не-
сколько иной форме, а именно в виде равенства:
φ(x,	, )≈	( )· (z, )	(6)
где абсцисса z также есть х/R(Ei), а æ(Еi)- некоторый “коэффициент растя-
жения” дозного распределения вдоль оси ординат, одинаковый для всех z и .
В отличие от условия (5), согласно		которому, - при фиксированном	, -

должно иметь место совпадение распределений доз по относительной глуби-

не, менее жёсткое условие (6) говорит лишь о пропорциональности этих распределений, т.е. об универсальности формы дозных кривых.

В диапазоне энергии от нескольких кэВ до 1÷2 МэВ (а по литературным данным, по-видимому, и до 2-3 МэВ) æ(Ei) оказывается медленно и монотонно убывающей с ростом E функцией. Имеет смысл определять лишь относительные величины æ(Ei), приняв для какой-либо энергии Ex æ(Ех)=1. Если, например, взять в качестве Ех 1 МэВ и положить æ(1МэВ)=1, то по экспериментальным данным /12/оказывается æ (80 кэВ)=1,40 (±10%).

Ввиду того, что функции φ(x, Еi, ) является относительным дозным распределением, φ(0, Еi, )=1. Поэтому для всех значений Еi, кроме Еx, равенство

(6) не может строго выполняться во всём диапазоне z(0≤z≤1). Для последую-

щих выводов достаточно потребовать, чтобы условие (6) выполнялось при

51

, N( )

всех z0,2 и это, действительно, имеет место для экспериментальных дозных распределений с точностью около 10%, т.е. с точностью лишь немного меньше тойскакойэтидозныераспределенияизвестны.Такимобразом,приближение

(6), хотя и выполняется не во всём диапазоне z, но значительно лучше соот-

ветствует экспериментальным данным, чем (5).

Объединяя (4) и (6), можно записать:
P(x, ,θ)≈	(		· (z, )	(7)

Полубесконечный блок, широкий пучок, распределение электронов N(θ)

Пусть на плоскую поверхность полубесконечного блока облучаемого материала падает широкий пучок моноэнергетических электронов с угловым распределением N( ). Иными словами, в соответствии с определением потока, величина N( )dΩ даёт количество электронов, летящих внутри элемента телесного угла dΩ с осью, образующей угол с нормалью к поверхности, и пересекающих за единицу времени единичную площадку, перпендикулярную оси dΩ. Тогда, создаваемую таким потоком мощность дозы на глубине x под

поверхностью можно записать в виде:
P(x, Ei)=	(	Ω	)		dΩ	(8)
В частном случае….

В частном случае, когда электронный поток (в отсутствии облучаемо-

го материала) - изотропный, причём полный (4					-) поток есть n, то величина
N( ) dΩ= ·2	sin d = sin d
При этомπ	выражение	для мощности дозы (Ри.п.) изотропного потока моноэ-
нергетических электронов примет вид:
	Ри.п.(x, )=				sin d	(9)
Тонкий источник с изотропной				миссией, полубесконечный блок

В другом интересующем нас частном случае, когда на поверхности полубесконечного блока лежит тонкий плоский источник с изотропной эмиссией, причём поверхностная плотность его “активности”есть

dΩ= tg d . Тогда мощность дозы от изотропного источника моноэнергетиче-

ских электронов запишется в виде:

лишь дозы

Ри.и.(x, )=

tg d

(10)

В случае, когда нас интересуют

на глубине x

0,2R (Ei) (10) c

учётом (7) перепишется в виде:

(11)

(z≥0,2)

( ) ) 1 ( )

Ри.и.(x,

)≈

(

·

(z,

)tg

d

Дозный коэффициент обратного рассеяния

Величины дозного коэффициента обратного рассеяния ∆ (Ei,

) могут быть

либо измерены, либо оценены по другим величинам характеризующим обрат-

ное рассеяние электронов. Результаты (и методика) измерения ∆ (Ei,

) для

ряда материалов, в том числе для плексигласа, и двух энергий Е (около 1 и

около 0,4 МэВ) приведены в /17/. Для расчётной оценки ∆ (Ei,

) можно вос-

52

Сигнальный экземпляр

пользоваться соотношением, вытекающим из определения этой величины:
	(Ei, )≈ (Ei, ) (Eср) / (Ei) cos	1 –1	(12)
Здесь	(Ei, )- обычный (“числовой”) коэффициент обратного рассеяния,
Еср- средняя энергия обратно рассеянных электронов,		- угол рассеяния (по

отношению к нормали к поверхности). Используя приведённые в литературе экспериментальные результаты (см. напр., обзор /62/, посвящённый обратному рассеянию электронов), можно оценить для тканеэквивалентного материала

все входящие в (12) сомножители при энергиях Ei в диапазоне ~ 0,02+ 2 МэВ и
углах падения					в интервале 0+900. Примеры необходимых данных приведены
в таблице 1 для двух значений													и трёх значений Ei:
																							Таблица 1
			Оценки параметров обратного рассеяния электронов
																	Ecp/Ei			сos			(cos		1	)-1
																										cp
	Энергия Еi							0,4				1		2	0,4		1		2	0,4			1			2
			(МэВ)
			=00			0,09						0,06		0,05	0,45		0,3		0,2	2			1,9			1,8
			=600			0,26						0,26		0,26	0,75		0,65		0,6	1			1			1
	Величины 1+∆ (Ei, ), полученные на основании этих оценок расчётом по
(12) (для плексигласа) даны в таблице 2:
												Значения 1+∆(Ei,					)						Таблица 2
			E МэВ										0,4				1						2
				0
				0								1,25(1,21)					1,15(1,15)						1,11
				60								1,28(1,23)					1,27(1,31)						1,26
	В скобках указаны экспериментальные значения 1+∆ из работы /17/. При
	) =
→			отношения									а также величина					, стремятся к 1.						Ввиду этого
( ,									и ,
							ср
	Из данных, представленных в таблице 2, видно, что зависимость величи-
ны 1+			( ,		от энергии E в диапазоне 0,4+2 МэВ довольно слаба,- она не
превышает				±6% даже при значенияхi											, близких к 00				и существенно умень-
шается начиная с							≈300. Энергетическая зависимость величины 1+∆(E, )
																										i

53

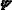
0,02МэВ≤Е<0,4МэВ выражена еще слабее, чем рассматриваемом диапазоне 0,4 E 2МэВ. Учитывая эти обстоятельства, величину 1+∆(Ei, ) при вычислении интеграла в (11) можно с достаточной точностью рассматривать как функциюлишьоднойпеременнойипринятьдляэтойвеличиныэкспериментальные/17/илирасчётные(12)значенияприэнергииEi,равной,например,1МэВ:

0	0	30	45	60	75	85	90
1+ (1МэВ, )0	1,15	1,24	1,26	1,31	1,60	1,95	2,00

Обозначение интеграла через F(z)

Учитывая, что интеграл в выражении (11) практически не зависит от Ei, мы обозначим его через F (z).

	F(z)=
Тогда Pи.и.≈		( )F(z) при				z		0,2.
Переход к функции		(r,		)	от распределения P (x,E)
Перейдём теперь от распределения							Pи.и. (x,E) к интересующейи.и.		нас функции
(r, ).	Если бы плоский тонкий изотропный источник был полностью (т.е.
с обеих	сторон) окружён тканеэквивалентным материалом, то связь между
функциями Pи.и. и была бы весьма простой. С помощью интегрирования не-
трудно установить, что:		и.и.							(13)
		∞	(x,		)=2		∞

Дозноераспределениеотплоскогоизотропногоисточникаобозначеноздесь

∞ , чтобы подчеркнуть, что в данном случае рассматривается источник, по-
гружённыйи.и.	в “бесконечную” среду. Решая (13) относительно , получим:
	(x,Ei)=- и∞.и.(x,	)	”	(14)
Разница между распределениями и∞и (x, ) и		ии (x,		), обусловленная об-
ратным рассеянием электронов от материала. . , “. над.				тонким источником,

должна практически исчезать при некотором удалении от источника. Ины-

ми словами, для каждого значения E		i	можно найти такую глубину x* (E				) что
						i
и∞и	(x, ) ≈		ии	(x,		) при х≥ x*	(15)
При этом (14) перепишется. . в виде		:	. .			) ( х≥ x* )
(x,Ei)	-		и.и.(x,				(16)

или после подставления выражения для Ри.и , в виде:

54

Сигнальный экземпляр

							i
W(r, )=4 r2 (r, ) - (		)		при	z		(17)
Выражение (17) должно	быть справедливым				значениях z=r/R(E), одно-
временно удовлетворяющих неравенствам: z		0,2 и z≥z*=x*/R(Ei)

“Граничное условие”(3) для функций W(r) (для бета-спектров) само является следствием аналогичных условий для функций W(r, EI). В /…..,121/ показано, что вблизи точечного изотропного источника моноэнергетических электронов в некотором интервале расстояний должно выполняться соотношение:

W(r, Ei) ,

(18)

Причём этот интервал расстояний ограничен сверху значением z 0,15, поскольку при указанном z левая часть (18) может на 10-12% (но не более) превышать правую.

Попробуем обойтись без оценки величин z*

Попробуем обойтись без оценки величин z*, выбрав следующий путь “конструирования” функции W(r,Ei). Образуем приближенную составную функцию W(r, Ei). Таким образом, чтобы она в области малых z, при z0≤z, определяясь выражением (18), а при больших z (z0≤z≤1)- выражением (17). При этом, как будет показано ниже, мы сможем определить точку “сшивки” z0 двух функциональных зависимостей. Если найденная величина z0 окажется близкой к 0,15+ 0,20, то, в соответствии со сказанным выше, такая приближённая составная функция будет достаточно хорошо (не более, чем с 10-15% ошибкой

в “переходной” области) соответствовать истинной функцииW(r, Ei). При этом
z* 0,2, и необходимости оценивать эту величину не будет.
Вычисление функции F(z) =	МэВ	ƒ	произво-
дилось путём численного интегрирования	. Использованный при этом “набор”

дозных распределений ƒ(z, ) /12/, соответствующих E=1МэВ, представлен на рис.2

Для нахождения двух функций, æ (Ei) и z0(Ei) можно использовать два урав-
нения:						(условие нормировки)		(19)
æ(Еi)=
	()
			(	условие «сшивки»			двух функциональных зависимостей
				−
при z0)								(20)

Учитывая, что W(r, Ei) определяется при z≤z0 по (18), а при z≥z0 -по (17),
условие (19) можно переписать в виде:
z0-æ(Eæ i) ( ) ( )	(21)

55

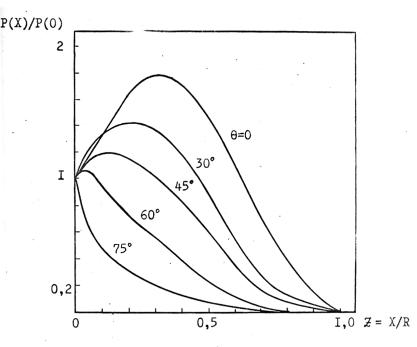
Функции æ(Ei) и z0 (Ei) найденные по ур-ниям (20) и (21) изображены на рис.3. При вычислении правой части в (21) для малых Е были использованы данные /123/ (для воды). То обстоятельство , что во всём интересующем нас диапазоне энергии E≤ 3 МэВ величина z0 оказалась достаточно близкой к 0,15+0,20, позволяет обойтись без оценок z*.

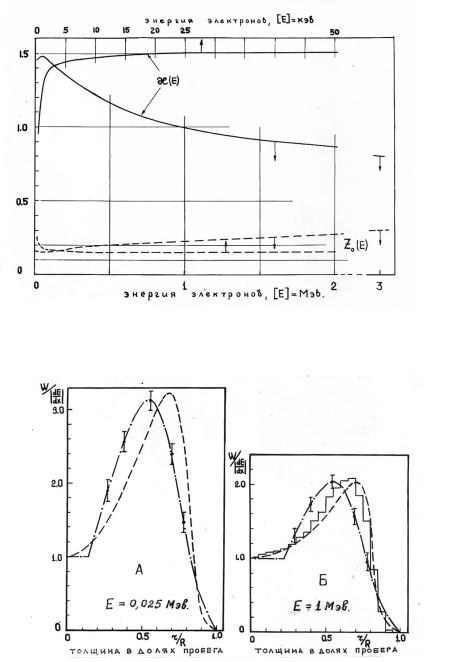
Дозовые функции точечного источника моноэнергетических электронов W(r, Ei) для энергий E=0,025 МэВ и 1 МэВ изображены штрих-пун-

ктирными кривыми на рис.4. По осям абсцисс здесь отложены расстояния от

источника в долях среднего пробега, т.е. z=z/R(Ei), по осям ординатотноше- ния W/ .

Обозначенные на рис.4 ошибки обусловлены главным образом дифференцированием функции F(z)/ ур-е (17). Шьриховые кривые на рис.4 изображают функции W(r,Ei) для тех энергий, вычисленные Спенсером для полистирола /66/. Видно, что различие штрих-пунктирных и штриховых кривых на рис.4 имеет такой же характер, как и в случае плоского источника (геометрия а) ), представленном на рис.1

Рис. 2. Зависимости функций Р(Х)/Р(0) от Z=X/R для различных углов падения электронов.

56

Сигнальный экземпляр

Рис. 3. Зависимости величин æ и Z0 от энергии электронов.

Рис. 4. Графики функции W(r/R, Ei)/ ) . .

Штрихпунктирная кривая – результат расчета по МЕДФ. Штриховая линия – результаты расчетов Спенсера. Гистограмма – данные расчета Бергера.

57

4 r2Ψ(r,Ei)=W(r,Ei)≈Ι (Ei)Ι

58

3.3. Расчёт функции точечного источника бета−излучения.

3.3.1. Расчёт по методу “единых дозовых функций”.

Как уже отмечалось выше значения функций Ψ(r) для бета−спектров любой формы и для любых расстояний r от источника можно рассчитать суммируя (интегрируя) по спектру дозные распределения для отдельных моноэнергетических линий:

Ψ(r) = ,здесь i−доляданноймонолииниивспектреиΨi−распределение поглощённой энергии для изотропного источника моноэнергетических электронов с энергией Ei. Основой для такого расчёта являются функ-

ции Ψi. Выше было показано, что в подобных расчётах предпочтительнее

использовать так называемый метод единых дозовых функций /ЕДФ/. В работах / / было найдено дозное поле от тонкого плоского изотропно

источника, лежащего на границе полубесконечной среды. Представим себе теперь, что плоский бесконечно тонкий и широкий изотропный источник электронов с энергией Ei находится внутри безграничного тканеэквивалентного материала. Обозначим создаваемое этим источником одномерное дозное распределение как Р∞(xi,Ei). Функция Р∞отличается от Р(xi,Ei) тем, что последнее соответствует пустому верхнему полупространству, в то время как распределение Р∞(соответствует случаю, когда над источником находится слой материала, рассеивающего излучение.

Электроны, испытавшие обратное рассеяние от лекгоатомного материала, лежащего над источником, обладают сравнительно низкой энергией ( в сред-

нем около 0,3 Е ), поэтому функции Р∞ и Р могут различаться между собой
i
лишь при малых расстояниях Х от источника, а при больших Х должны прак-
тически совпадать.
Функция Р∞ и интересующая нас функция Ψ(r, Е						i)	связаны соотношением:
Ψ(r, Ei) = −		·					(9)
(вывод ф-лы см. на стр. 23)

В области больших r æ∞(x, Еi), поэтому здесь, учитывая (7)−(9), можно написать

4 r2Ψ(r,Ei)=W(r,Ei)≈−Ι (Ei)Ι[1+Δ(Ei)]z

(10)

Вблизи точечного источника многоэнергетических электронов с энергией Еi, находящегося в однородной легкоатомной среде, в соответствии с доводами, изложенными несколько ниже, должно выполняться условие, аналогичное

(3):

(11)

при r ≤ r0

Сигнальный экземпляр

Построим приближенную составную функцию точечного источника моноэнергетических электронов, определяемую в области малых r соотношением (II), а в области r−соотношением (I0). При этом для простоты предположим, что промежуточная область, в которой не выполняется ни (10), ни (II), вообще отсутствует. Допустимость этого предположения будет обоснована ниже. Перепишем сформулированные условия, приняв для приближенной функции старое обозначение W(r, Ei):

W(r,Ei)=Ι (Ei)Ι

W(r,Ei)=Ι (Ei)Ι при r ≥ r0		(12)

где r0− точка “сшивки” двух функциональных зависимостей.

Поскольку функция F(z) известна, для определения W( r, Ei) достаточно оценитьΔ(Ei) и r0 (Ei) ( или−вместо r0(Ei)− функцию z0(Ei)=r0/R (Ei)).

НайтиΔ(Ei) и z0(Ei) можно из двух уравнений:

ǡ )dr=Ei			(условие нормировки)	(13 а)
−[1+Δ(Ei)]z0		=1	( условие сшивки при z=z0)	(13б)

Уравнение (13а) после интегрирования с учётом (12) перейдёт b:

−[1+Δ(Ei)][F(z0) z0 +

=

( )

Что, принимая во внимание (13б), можно записать в виде:

Z0−	( ) ( )		=
		( )
				│ (
				) │ ( )

(14)

(15)

Cоотношение (15) позволяет найти функцию z0(Ei) и далее, с помощью

(13б)−функциюΔ(Ei) .

Вычисление функции Δ(Ei) и z0(Ei) представлены на рис. № 2. Начальные участки кривых ( область энергий ниже 15 кэВ) изображены отдельно. Значения ионизационных потерь (Ei) (Ei) (для воды) получены из…..

Нарис№1а,б,вштрих−пунктиромизображеныграфикиполученнойфункцииW(r, Ei) для воды и трёх значений энергии электронов Ei−0,025; 1 и 2 МэВ.

Поосямабсциссотложенорасстояниеотисточникавдоляхпробега,т.е.r/R, по оси ординат−отношение W(r, Ei)/ l (Ei)l.

Штриховые кривые на рис. № 1 а,б,в вычислены в работе /11/для полистирола с использованием приближения непрерывного замедления. Гистограмма (дляEi=IМэВ)построенаподаннымработы/13/(расчётметодомМонте−Карло для воды, приближение непрерывного замедления). Как видно, полученная намидляслучаягеометрииб)функцияW(r,Ei)отличаетсяотсоответствующих

59