Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

Санкт-Петербургский государственный лесотехнический университет имени С.М. Кирова

Отчет

По дисциплине: «СИСТЕМЫ КОМПЬЮТЕРНОЙ МАТЕМАТИКИ»

Ответы на вопросы

Выполнил:

Королев Александр Анатольевич

студент факультета ИУиЭЛС

2 курса, Заочное отделение

№ зачетной книжки 56186

Проверил:

доц. Втюрин В.А.

Санкт-Петербург

2015 - 2016 уч. год.

Системы компьютерной математики

Что такое СКМ?

СКМ – Системы компьютерной математики.

Под универсальной СКМ понимаются, как правило, программные продукты, позволяющие проводить алгебраические преобразования над объектами достаточно общей, в математическом смысле, природы.

Как различаются СКМ?

Одно из основных отличий СКМ от традиционных систем программирования связано с процессом численного решения уравнений. Обычно значения вычисляются в 2 этапа, в начале вместо входящих в выражения переменных подставляются их значения, а затем вычисляется все выражение.

СКМ же, например, при решении линейных алгебраических уравнений выделит все его точные рациональные и алгебраические решения, даже если коэффициенты уравнения зависят от буквенных параметров, в то время как, самое большее на что можно рассчитывать, используя численные методы – это протабулировать решение уравнения при различных значениях этих параметров.

Что умеют СКМ?

Возможности, представляемые пользователю современными СКМ охватывают многие разделы алгебры и математического анализа. Во многих системах можно выполнять:

– арифметические операции с целыми (произвольной длины), рациональными, действительными и комплексными числами;

– алгебраические операции с полиномами и рациональными функциями одной или нескольких переменных;

– вычислять наибольший общий делитель полиномов;

– выполнять факторизацию над полем рациональных чисел.

Многие действия математического анализа доступны СКМ:

– дифференцирование, включая нахождение частных производных;

– интегрирование элементарных функций;

– разложение в ряды и многое др.

В СКМ имеются встроенные операции над матрицами с символьными элементами:

– сложение, умножение;

– обращение матриц;

– вычисление определителей;

– решение систем линейных алгебраических уравнений.

Пользователь СКА обладает возможностью:

– управлять процессом упрощения математических выражений;

– выполнять подстановки;

– выделять части формул;

– получать численные значения формул.

Какие знаете известные СКМ, и дать им краткую характеристику?

Наиболее известными на сегодняшний день среди универсальных СКМ являются MatLab, MathCAD, Maple, Mathematica и Derive.

MATLAB выполняет множество компьютерных задач для поддержки научных и инженерных работ, начиная от сбора и анализа данных до разработки приложений. Среда MATLAB объединяет математические вычисления, визуализацию и мощный технический язык. Встроенные интерфейсы позволяют получить быстрый доступ и извлекать данные из внешних устройств, файлов, внешних баз данных и программ.

MATLAB имеет широкий спектр применений, включая цифровую обработку сигналов и изображений, проектирование систем управления, естественные науки, финансы и экономику, а также приборостроение. Открытая архитектура позволяет легко использовать MATLAB и сопутствующие продукты для исследования данных и быстрого создания конкурентоспособных пользовательских инструментов.

Основные функции:

– быстрые и точные численные алгоритмы;

– графика для анализа и отображения данных;

– интерактивный язык и среда программирования;

– инструменты для настройки пользовательских интерфейсов;

– интерфейсы с внешними языками, такими как С, С++, Fortran и Java;

– поддержка импорта данных из файлов и внешних устройств плюс доступ к базам данных и вспомогательному оборудованию при помощи приложений;

– преобразование MATLAB приложений в С и С++.

Численные алгоритмы быстрые, точные и надежные. Эти алгоритмы, разработанные экспертами в математике, являются фундаментом языка MATLAB. Математика оптимизирована для матричных и векторных операций, так что она может быть использована вместо языков более низкого уровня, подобных С и С++, при этом получается та же скорость вычислений при значительной экономии времени на программирование.

Mathcad– это многофункциональная интерактивная вычислительная система, позволяющая, благодаря встроенным алгоритмам, решать аналитически и численно большое количество математических задач не прибегая к программированию. Рабочий документ Mathcad – электронная книга с живыми формулами, вычисления в которой производятся автоматически в том порядке, в котором записаны выражения. Отличается простым и удобным интерфейсом, написанием выражений стандартными математическими символами, хорошей двух- и трехмерной графикой, возможностью подключения к распространенным офисным и конструкторским программам, а также к Internet.

Программа Mathcad сочетает в себе набор мощных инструментов для технических расчетов с полиграфическим качеством написания формул и гибкий, полнофункциональный текстовый редактор. С помощью эффективной среды решения задач программы Mathcad можно выполнять работу и демонстрировать результаты в одном и том же документе – на рабочей страннице Mathcad. В отличие от другого технического программного обеспечения Mathcad осуществляет математические расчеты в той же последовательности в которой Вы их записываете. Вводятся уравнения, данные для построения графика функции и текстовые примечания в любом месте страницы, при этом математические выражения в Mathcad записываются в полиграфическом формате. Единственная разница с обычным текстом, включающим математические формулы и графики состоит в том, что Mathcad уравнения и графики – «живые». Изменение значений переменных, данных графика или уравнений приведет к немедленному перевычислению рабочей страницы.

Maple– это мощная вычислительная система, предназначенная для выполнения сложных вычислительных проектов как аналитическими так и численными методами. Maple содержит проверенные, надежные и эффективные символьные и численные алгоритмы для решения огромного спектра математических задач, включая широко известные библиотечные численные алгоритмы компании NAG (NumericAlgorithmGroop). Maple умеет выполнять сложные алгебраические преобразования и упрощения над полем комплексных чисел, находить конечные и бесконечные суммы, произведения, пределы и интегралы, решать в символьном виде и численно алгебраические (в том числе трансцендентные) системы уравнений и неравенств, находить все корни многочленов, решать аналитически и численно системы обыкновенных дифференциальных уравнений и уравнений в частных производных. В Maple включены пакеты подпрограмм для решения задач линейной и тензорной алгебры, Евклидовой и аналитической геометрии, теории чисел, теории вероятностей и математической статистики, комбинаторики, теории групп, интегральных преобразований, численной аппроксимации и линейной оптимизации (симплекс метод) а также задач финансовой математики и многих, многих других задач.

Maple обладает также развитым языком программирования. Это дает возможность пользователю самостоятельно создавать команды и приложения и таким образом расширять возможности Maple для решения специальных задач.

Для технических применений в Maple включены справочники физических констант и единицы физических величин с автоматическим пересчетом формул. Хороший текстовый редактор, полиграфическое качество формул и превосходная двух- и трехмерная графика позволяют профессионально оформить выполненную работу и сохранить ее либо в виде электронного документа (HTML) для опубликования в Интернет либо стандартного текстового документа (rtf).

Mathematicaявляется одной из универсальных математических систем, которая дает возможность решать большое количество весьма сложных задач не вдаваясь в сложности программирования. В ряду себе подобных Mathematica является одной из самых мощных и детально разработанных. С ее помощью легко осуществляются численные и символьные вычисления. Сильной стороной системы, выгодно отличающей ее от остальных, является двух и трехмерная графика, применяемая для визуализации кривых и поверхностей в трехмерном пространстве.

В среде Mathematica содержится язык программирования современного высокого уровня с более емким и естественным функциональным стилем и стилем правил преобразований.

Система интерактивна (то есть работает в режиме постоянного диалога с пользователем). Она гибка и универсальна в том смысле, что может быть использована всеми желающими, как студентами, так и профессионалами математиками и другими специалистами, работа которых связана с математикой.

DERIVE – самая маленькая из систем компьютерной алгебры. Последняя версия Derive под MS-DOS может работать на «древних» ПК даже без жесткого диска, целиком помещаясь на загрузочной дискете. При этом система имеет многооконный интерфейс и управляется простой системой меню. Derive тщательно опробованная, надежная и быстрая система. Ядро Derivecодержит около 1000 функций и 23 тысячи строк программного кода. Удивительная компактность ядра связана с использованием языка программирования экспертных систем LISP.

Derive является универсальной математической системой, ориентированной на решение широкого круга математических и научно-технических задач. Современные версии Derive – это расширяемые системы, способные легко адаптироваться под решение специальных задач. Они поставляются с развитой библиотекой функций, существенно расширяющей возможности системы. Derive позволяет готовить расширения и записывать их в виде файлов.

Формат представления вещественных чисел

Арифметические операции

1.Сложение:

» 320+10

ans =

330

2.Умножение:

» 7^3

ans =

21

» t=ans^0.3

t =

6.3

Комплексные числа

1.Зададим комплексные числа:

» а=2 + i

а =

2 + li

» b = 5 - 4i

b =

5 - 4i

2.Вычислим произведение комплексных чисел

» а* b

ans =

14 - 3i

3.Вычислим√a

» d = sqrt(a)

d = 1.4553 + 0.3436i

4.Вычислим b3

» b^3

ans =

-1.1500e+002 -2.3600e+002i

5.Вычислим | a |

» abs(a)

ans = 2.2361

6.Вычислим действительную (re(b)) и мнимую (im(b)) части комплексного числа

» real(b)

ans =

5

» imag(b)

ans =

-4

7.Вычислим аргумент комплексного числа (arg(a))

>> angle(a)

>> a=2+i

a =

2.0000 + 1.0000i

>>angle(a)

ans =

0.4636

>> b = 5 - 4i

b = 5.0000 - 4.0000i

8.Вычислим число комплексно сопряженное числу b

>>conj(b)

ans =

5.0000 + 4.0000i

9.Вычислимsin(a)

>>sin(a)

ans =

1.4031 - 0.4891i

Векторы и матрицы

1.Зададим вектор-строку:

>> u1=[3 3 3]

u1 =

3 3 3

>>whos u1

Name Size Bytes Class

u1 1x3 24 double array

Grand total is 3 elements using 24 bytes

2.Зададим вектор-столбец:

>> u2=[2;1;-2]

u2 =

3

2

-4

>>whos u2

Name Size Bytes Class

u2 3x1 24 double array

Grand total is 3 elements using 24 bytes

3.Зададим, вектор с использованием числового диапазона:

>>dialp=4.6:0.7:6.546;

>>dialp

dialp =

4.6000 5.3000 6.0000

>>length(dialp)

ans =

3

4. Вычислим скалярное произведение векторов

>> a=[2 3 5];

>> b=[5 7 1];

>> a*b'

ans =

36

5. Поэлементное умножение векторов

>> a=[2 3 5];

>> b=[5 7 1];

>> a.*b

ans =

10 21 5

6. Создадим матрицу

>> A=[-3 4 6;2 -2 4;-5 8 7]

A =

-3 4 6

2 -2 4

-5 8 7

7. Выделим заданный столбец матрицы

>> A(:,1)

ans =

-3

2

-5

8. Выделим заданную строку матрицы

>>A(2,:)

ans =

2 -2 4

9.Выделим определитель матрицы

>>det(A)

ans =

38

10.Вычислим обратную матрицу

>>inv(A)

ans =

-1.2105 0.5263 0.7368

-0.8947 0.2368 0.6316

0.1579 0.1053 -0.0526

Элементарные функции

>> x=0:0.06:pi/2;

>> y=cos(x);

>>whos x y

Name Size Bytes Class Attributes

x 1x27 216 double

y 1x27 216 double

Grand total is 316 elements using 2528 bytes

>> Аналогично вычисляются функции от двумерных массивов:

>> A=[3 pi/5; pi/3 pi/4; 7*pi/2 5*pi/5]

A =

3.0000 0.6283

1.0472 0.7854

10.9956 3.1416

>>sin(A)

ans =

0.1411 0.5878

0.8660 0.7071

-1.0000 0.0000

2.1 Функции MATLAB для создания

передаточных функций звеньев системы

Функция tf()

Процедуры образования передаточной функции W(S) имеют вид:

» n=[0.45];

» m= [14470 268 2] ;

» W=tf(n,m)

После нажатия клавиши <Enter> на экране появится передаточ¬ная функция в виде:

» n=[0.45];

» m= [14470 268 2] ;

» W=tf(n,m)

Transfer function:

0.45

---------------------

14470 s^2 + 268 s + 2

Функции pole()

ФункциюW=tf (n,m) можно также представить в следующем виде:

»W=tf( [0.45], [14470 268 2])

>> P=pole(W)

P =

-0.0093 + 0.0072i

-0.0093 - 0.0072i

Функцииroots() и poly()

Найти корни уравнения 7S3 + 3S2 + 5 и по корням восстановить полином.

В данном случае P=[7 3 0 5] и процедуры решения будут иметь вид:

>> P=[7 3 0 5];

>> r=roots(P)

r =

-1.0620

0.3167 + 0.7565i

0.3167 - 0.7565i

>> P=poly(r)

P =

1.0000 0.4286 -0.0000 0.7143

Функцияconv()

p(s) = 5s2 +6s + 4 и q(s) = 8s + 5

>> p=[5 6 4];

>> q=[8 5];

>> G=conv(p, q)

G =

40 73 62 20

Или

G = 40s3 + 73s2 + 62s + 20

Функцияpolyval ()

P(s) = 5s2 + 6s + 4

При s= -6.

Решение:

>> n=[5 6 4];

>> z=polyval(n, -6)

z =148

Операции с передаточными функциями звеньев

Сложение передаточных функций

Решение:

>> n1=[16];

>> m1=[3 2 8];

>> q1=tf(n1,m1)

Transfer function:

Transfer function:

16

---------------

3 s^2 + 2 s + 8

>> n2=[5 12 30];

>> m2=[2 6 7 1];

>> q2=tf(n2,m2)

Transfer function:

5 s^2 + 12 s + 30

-----------------------

2 s^3 + 6 s^2 + 7 s + 1

>> Q=q1+q2

Transfer function:

15 s^4 + 78 s^3 + 250 s^2 + 268 s + 256

-------------------------------------------

6 s^5 + 22 s^4 + 49 s^3 + 65 s^2 + 58 s + 8

Функцияpz map ()

Transfer function:

15 s^4 + 78 s^3 + 250 s^2 + 268 s + 256

-------------------------------------------

6 s^5 + 22 s^4 + 49 s^3 + 65 s^2 + 58 s + 8

Решение:

>> n=[15 78 250 268 256]; m=[6 22 49 65 58 8];

>> q=tf(n, m)

Transfer function:

15 s^4 + 78 s^3 + 250 s^2 + 268 s + 256

-------------------------------------------

6 s^5 + 22 s^4 + 49 s^3 + 65 s^2 + 58 s + 8

>>pzmap(q)

Рис. 2.7. Определение нулей и полюсов передаточной функци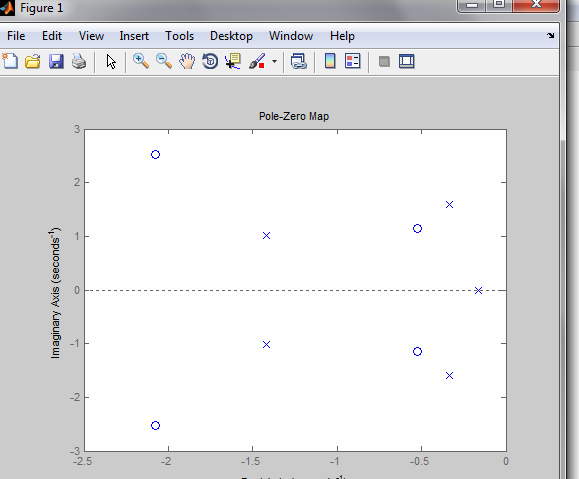

Функция series ()

Решение:

>> n1=[23465 76 1];

>> m1=[235 0];

>> q1=tf(n1,m1);

>> n2=[0.8];

>> m2=[235 1];

>> q2=tf(n2,m2);

>> Q=series(q1,q2)

Transfer function:

18772 s^2 + 60.8 s + 0.8

------------------------

55225 s^2 + 235 s

Функция parallel ()

Решение:

>> n1=[23465 76 1];

>> m1=[235 0];

>> q1=tf(n1,m1);

>> n2=[0.8];

>> m2=[235 1];

>> q2=tf(n2,m2);

>> Q=parallel(q1,q2)

Transfer function:

5.514e006 s^3 + 41325 s^2 + 499 s + 1

-------------------------------------

55225 s^2 + 235 s

Функция feedback ()

>> n1=[23465 76 1];

>> m1=[235 0];

>> q1=tf(n1,m1);

>> n2=[0.8];

>> m2=[235 1];

>> q2=tf(n2,m2);

>> Q=series(q1,q2)

Transfer function:

18772 s^2 + 60.8 s + 0.8

------------------------

55225 s^2 + 235 s

>>feedback(Q, [1])

Transfer function:

18772 s^2 + 60.8 s + 0.8

-------------------------

73997 s^2 + 295.8 s + 0.8

>> n1=[23465 76 1];

>> m1=[235 0];

>> q1=tf(n1,m1);

>> n2=[0.8];

>> m2=[235 1];

>> q2=tf(n2,m2);

>>feedback(q1,q2,-1)

Transfer function:

5.514e006 s^3 + 41325 s^2 + 311 s + 1

-------------------------------------

73997 s^2 + 295.8 s + 0.8

Алгебра вектор и матриц

Создание векторов и матриц

Пример 1

>> [-4,-6,2, 7,8]

ans =

-4 -6 2 7 8

>> v=[45+7i 8-9i 2]

v =

45.0000 + 7.0000i 8.0000 - 9.0000i 2.0000

Пример 2

>> M = [5 2 8; 2 -4 1; -6 3 8]

После нажатия клавиши <Enter> на экране появится следующая матрица:

M =

5 2 8

2 -4 1

-6 3 8

>> M = [8-4i,2+i,14;6,8,5;i,3,-i]

А теперь матрица выглядит так:

M =

8.0000 - 4.0000i 2.0000 + 1.0000i 14.0000

6.0000 8.0000 5.0000

0 + 1.0000i 3.0000 0 - 1.0000i

Пример 3

>>V = [1:5]

V = 1 2 3 4 5

>> M=[1:3;2:4;7:9]

M =

1 2 3

2 3 4

7 8 9

>> V=[1:0.7:3]

V =

1.0000 1.7000 2.4000

>> M=[2:0.3:2.8;2:0.8:3.7;4:6]

M =

2.0000 2.3000 2.6000

2.0000 2.8000 3.6000

4.0000 5.0000 6.0000

Вызов на экран и замена элементов матрицы

Пример 4

>> v=[2 4 5 8 13];

>> v(5)

ans =

13

>> M=[2,3,6; 4 7 11; -2,8, 4];

>> M(2,2)

ans =

7

Пример 5

>> v(5)=6

v =

2 4 5 8 6

>> M(3,1)=10

M =

2 3 6

4 7 11

10 8 4

Изменение размера вектора или матрицы

Пример 6

Пусть матрица имеет вид

>> M=[2 5 6;3 8 5;4 13 -9]

M =

2 5 6

3 8 5

4 13 -9

Необходимо удалить вторую строку и третий столбец.

Решение будет иметь вид:

>>M(5,:)

ans =

4 13 -9

>> M(:,2)

ans =

5

8

13

Пример 7

Пусть имеются три следующих вектора:

>>V1= [ 4 5 6]

V1 =

4 5 6

>>V2=[2 -6 4]

V2 =

2 -6 4

>>V3=[8 5 3]

V3 =

8 5 3

>>M=[V1;V2;V3]

M =

4 5 6

2 -6 4

8 5 3

>>Z=[M, M+3; M-5, M*2]

Z =

4 5 6 7 8 9

2 -6 4 5 -3 7

8 5 3 11 8 6

-1 0 1 8 10 12

-3 -11 -1 4 -12 8

3 0 -2 16 10 6

4.2.3. Математические операции с векторами и матрицами

Определитель матрицы

Пример 8

>> M=[4 5 -3;2 -7 3;3 4 6];

>>det(M)

ans =

-90

>> M=[1+2i, 3, -2.5;i,-1,5;3,5,0];

>>det(M)

ans =

12.5000 -62.5000i

Транспортирование матрицы

Пример 9

Пусть исходная матрица имеет вид

>> M=[1+2i, 3, -2.5;i,-1,5;3,5,0];

>> Z=M'

Z =

1.0000 - 2.0000i 0 - 1.0000i 3.0000

3.0000 -1.0000 5.0000

-2.5000 5.0000 0

Следматрицы

Пусть матрица имеет вид:

>>M=[3 4 -1; 6 7 8; 2 -3 1]

M =

3 4 -1

6 7 8

2 -3 1

>>M=[3 4 -1; 6 7 8; 2 -3 1];

>>Z=trace(M)

Z = 11

Обратная матрица

Пример 11

>>M=[3 4 -1; 6 7 8; 2 -3 1];

>> Z=inv(M)

Z =

0.1879 -0.0061 0.2364

0.0606 0.0303 -0.1818

-0.1939 0.1030 -0.0182

Единичная матрица

Пример 12

>> M=eye(4)

M =

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1

>>M=eye(3,4)

M =

1 0 0 0

0 1 0 0

0 0 1 0

>> M=[2 2 3 4;3,3,-4,7;0,2,3,0;2,3,4,5];

>> M=eye(size(M))

M =

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1

Образование матрицы с единичными элементами

Пример 13

>> M=ones(4)

M =

1 1 1 1

1 1 1 1

1 1 1 1

1 1 1 1

>> M=ones(3,5)

M =

1 1 1 1 1

1 1 1 1 1

1 1 1 1 1

>> M=[5,6,1,7;8,1,-3,5];

>> Z=ones(size(M))

Z =

1 1 1 1

1 1 1 1

Образование матрицы с нулевыми элементами

Пример 14

>> M=zeros(3)

M =

0 0 0

0 0 0

0 0 0

>> M=zeros(3,4)

M =

0 0 0 0

0 0 0 0

0 0 0 0

>> M=[1,2,3;2,3,4;3,4,5];

>> M=zeros(size(M))

M =

0 0 0

0 0 0

0 0 0

Вектор равностоящих точек

Пример 15

>>R=linspace(1,2)

R =

1.0000 1.0101 1.0202 1.0303 1.0404 1.0505 1.0606 1.0707 1.0808 1.0909 1.1010……………………………………………………1.9596 1.9697 1.9798 1.9899

>> R=linspace(2,11,6)

R =

2.0000 3.8000 5.6000 7.4000 9.2000 11.0000

Перестановка элементов матрицы

Пример 16

>>M=[2,2,4,5;4,2,6,3]

M =

2 2 4 5

4 2 6 3

>>Z=fliplr(M)

Z =

5 4 2 2

3 6 2 4

>>W=flipud(M)

W =

4 2 6 3

2 2 4 5

Пример 17

>>V=[3,2,6];

>>P=perms(V)

P =

6 2 3

6 3 2

2 6 3

2 3 6

3 2 6

3 6 2

Создание матриц с заданной диагональю

Пример 18

>>V=[3,2,6];

>>M=diag(V,0)

M =

3 0 0

0 2 0

0 0 6

>> Z=diag(V,-4)

Z =

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0 0

3 0 0 0 0 0 0

0 2 0 0 0 0 0

0 0 6 0 0 0 0

>> V=diag(M,0)

V =

3

2

6

>> M=[2,2,4,5;4,2,6,3];

>> V=diag(M,1)

V =

2

6

>> V=diag(M)

V =

2

2