2298 ЭИ

б)

lim

2x + 1 −

x + 6 ;

в)

lim (7 − 6x)3 x−3 ;

г)

lim 1− cos 4x .

2 x

2x2 − 7x − 15

x→5

x→∞

x→0

1− cos8x

14.5. а) lim

3x2

+ 11x + 10

при x0

= −5 ,

x0 = −2 ,

x0 → ∞ ;

2x

2 + 5x +

2

x→ x0

3x + 17 −

2x + 12

x2 + 5 x2 / 2

1

− cos x

б)

lim

x2 + 8x + 15

;

в)

lim

;

г)

lim

x→−5

x→∞ x2 − 1

x→0

xsin x

14.6. а) lim

4x2

− 7x − 2

при x0

= 0 , x0 = 2 ,

x0

→ ∞ ;

2x2 − x − 6

x→ x0

x

x + 12 − 4 − x

1+ 6x

1− cos 6x

б)

lim

x2 + 2x − 8

;

в)

lim

;

г)

lim

.

x→−4

x→∞ 6x + 5

x→0

1

− cos 2x

	14.7. а)		lim		x2 + x − 12
					4x	2 −13x + 3
			x→ x0
б)	lim	x + 10 −				4 − x ;	в)
	x→−3	2x2 − x − 21
	14.8. а)		lim		3x2 + 5x − 8
					2x	2 + 3x − 5
			x→ x0
б)	lim	2 − x −			x + 6 ;		в)
	x→−2		x2 − x − 6
	14.9. а)		lim		x2	− 3x − 10
					2x	2 + 5x + 2
			x→ x0

	при x0 = 1 ,					x0 = 3 ,	x0 → ∞ ;
lim(2x − 3)				3	;		г) lim x ctg5x .
			x−2
x→2							x→0
	при x0			= −2 , x0 = 1 , x0 → ∞ ;
	2x −1 x / 3						lim 5x ctg3x .
lim				;		г)
x→∞ 2x + 4							x→0
	при x0			= 4 ,		x0 = −2 , x0 → ∞ ;

б) lim

3 + 2x −

x + 4

;

в)

lim

5

ln(2x − 5)

;

3x2 − 4x + 1

− 3

x→1

x→3 x

14.10. а) lim

7x2 − 6x − 1

при x0 = 3 ,

x2 + 4x − 5

x→ x0

7 ln(3x − 7)

б) lim

x2 + x − 12

;

в)

lim

;

4 − x

x − 3

x→3 x − 2 −

x→3

tg2 x

г) lim 2 .

x→0 x2

x0 = 1 , x0 → ∞ ;

г) lim 1− cos 4x . x→0 2x tg2x

14.11.

а)

lim

2x2

+ 3x − 2

при x

= 3,

x

= −2, x → ∞ ;

x→ x0 3x2

+ 2x − 8

0

0

0

4x+1

3x − 2 − 2

3

б)

lim

x2

;

в)

lim 1

+

;

г)

lim sin 3x ctg2x .

− 4

2x − 1

x→2

x→∞

x→0

14.12.

а)

lim

3x2

− 5x + 2

при x

= 4,

x

= 1,

x → ∞ ;

x→ x0 2x2 − x − 1

0

0

0

51

б)

б)

б)

б)

б)

б)

б)

б)

x + 4

− 1

2

2x−1

1− cos 4x

lim

;

в)

lim 1−

;

г)

lim

.

x→−3

3 − 2x − 3

x→∞

x +

4

x

→0

sin 2

3x

14.13.

а)

lim

10x

− 3x2 − 8

при x

= −3,

x

= 2,

x

→ ∞ ;

x→ x0 3x2

− 8x + 4

0

0

0

3x−4

x −

2

+ 2x

2x − 3

arcsin 6x

lim

x

;

в)

lim

;

г)

lim

.

x→∞

x→∞

2x + 1

x

→0

2x

14.14.

а)

lim

x2

− x − 2

при x

= 4,

x

= −1,

x

→ ∞ ;

x→ x0 2x2

− 5x + 4

0

0

0

4− x

x + 6 − 2

3x + 2

sin 2x

lim

x2

;

в)

lim

;

г)

lim

.

− 4

3x + 5

tg3x

x→−3

x→∞

x

→0

14.15.

а)

lim

7x

− x2 −12

при x

= −1,

x

= 3,

x

→ ∞ ;

x→ x0 2x2

−11x + 15

0

0

0

x+ 2

2

2

arctg3x

lim

4x

+ x − 2x

;

в)

lim 1−

;

г)

lim

.

x→∞

x→∞

3x − 1

x

→0

2x

14.16.

а)

lim

3 − 8x − 3x2

при x

= 2,

x

= −3,

x

→ ∞ ;

x→ x0 x2

+ x − 6

0

0

0

3x−2

x

− 2

2x −1

x tg5x

lim

;

в)

lim

;

г)

lim

.

2x + 1 − 3

2x + 5

x→4

x→∞

x

→0 sin 2 3x

14.17.

а)

lim

2x2

+ 7x − 4

при x

= 2,

x

= −4,

x

→ ∞ ;

x→ x0 4 −

3x − x2

0

0

0

2x−4

2x + 3

− 3

3x −1

sin 5x

lim

;

в)

lim

;

г)

lim

.

2 −

x + 1

3x + 2

x→0

x→∞

x

→0 sin 3x

14.18.

а)

lim

2x2

− 17x + 35

при x

= −3,

x

= 5,

x

→ ∞ ;

x→ x0

x2 − x − 20

0

0

0

4− x

9 − x − 3

2x − 3

sin 6x

lim

;

в)

lim

;

г)

lim

.

x + 4 −

2

2x + 1

tg2x

x→0

x→∞

x

→0

14.19.

а)

lim

9x − 2x2 −10

при x

= −5,

x

= 2,

x

→ ∞ ;

x→ x0

x2 − x − 2

0

0

0

x2 + 9

− 3

2

1−3x

tg2 3x

lim

;

в)

lim 1−

;

г)

lim

.

x→0

4 − x2

− 2

x→∞

3x − 1

x

→0

2sin 2

2x

14.20.

а)

lim

3x2 + 2x − 1

при x

= 2,

x

= −1,

x

→ ∞ ;

x→ x0

x3 + 1

0

0

0

52

б)

б)

б)

б)

б)

б)

б)

б)

5 − x

2 + 9

2

1−6x

3x

lim

;

в)

lim

1

+

;

г)

lim

.

2x +

1 − 3

3x

− 4

x→0

x→∞

x→0 sin 2x

14.21.

а)

lim

2x2 − 5x − 3

при x0

= 2,

x0 = 3,

x0 → ∞ ;

3x2

−

4x −15

x→ x0

2n − 3 3n+ 2

x −1 − 7 − x

3x

lim

х− 4

;

в)

lim

;

г) lim

.

x→4

x→0 arctg4x

n→∞ 2n + 5

14.22.

а)

lim

4x2

−

7x − 2

при x0

= 0,

x0 = 2,

x0 → ∞ ;

2x2 − x − 6

x→ x0

2n−7

х− 2

tg2x

3n + 2

lim

;

в)

lim

;

г) lim

.

x→2

x + 2 −

6 − x

x→0 sin 5x

n→∞ 3n

− 4

14.23.

а)

lim

2x2

+

5x − 3

при x0

= 3,

x0 = –3, x0 → ∞ ;

x2 + 5x + 6

x→ x0

4n+ 2

x −1 −

9 − x

ctg3x

n − 6

lim

х− 5

;

в)

lim

;

г) lim

.

x→5

x→0 ctg6x

n→∞ n − 4

14.24.

а)

lim

3x2

+ 11x + 10

при x0

= –3,

x0 = –2, x0 → ∞ ;

2x2 + 5x + 2

x→ x0

n−3

х− 2

4x

5n − 3

lim

;

в)

lim

;

г) lim

.

x→2

x + 3 −

7 − x

x→0 arcsin 5x

n→∞ 5n

+ 6

14.25.

а)

lim

3x2

−14x + 8

при x0

= 2,

x0 = 4,

x0 → ∞ ;

2x2

− 7x − 4

x→ x0

3n+5

x + 7 − 3 − x

lim tg2x ctg3x;

4n −

5

lim

х− 5

;

в)

г) lim

.

− 3

x→−2

x→0

n→∞ 4n

14.26.

а)

lim

4x2

− 25x + 25

при x0

= 2,

x0 = 5,

x0 → ∞ ;

2x2

−

15x + 25

x→ x0

5n+3

х+ 1

n − 4

lim

;

в)

lim sin 6x ctg2x;

г) lim

.

x→−1 x + 5 − 3 − x

x→0

n→∞ n + 5

14.27.

а)

lim

7x2

+ 26x − 8

при x0

= 1,

x0 = –4, x0 → ∞ ;

2x2 + x − 28

x→ x0

4n−5

x + 4 −

8 − x

arctg7x

2n −

5

lim

;

в)

lim

;

г) lim

.

x→2

х− 2

x→0

5x

n→∞ 2n

+ 3

14.28.

а)

lim

2x2

+ 15x + 25

при x0

= 5,

x0 = –5, x0 → ∞ ;

x2 + 15x + 50

x→ x0

53

х− 4

tg5x

3n −1

2n+3

б)

lim

x − 2 −

6 − x

;

в)

lim

;

г) lim

.

x→4

x→0 tg4x

n→∞ 3n + 6

14.29.

а)

lim

3x2

+ 5x − 8

при x0 = –2,

x0 = 1, x0 → ∞ ;

+ 3x − 5

x→ x0 2x2

n+4

x − 2 −

4 − x

sin 3x

5n − 3

б)

lim

х− 3

;

в)

lim

;

г) lim

.

tg2x

x→3

x→0

n→∞ 5n + 4

14.30.

а)

lim

6x2

+ 13x + 7

при x0 = –2,

x0 = –1, x0 → ∞ ;

+ 8x + 5

x→ x0 3x2

5n−1

x − 3 −

9 − x

arcsin 8x

4n + 1

б)

lim

;

в)

lim

;

г) lim

.

x→6

х− 6

x→0

4x

n→∞ 4n − 3

З А Д А Н И Е № 1 5

Задана функция y = f (x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.

1− x,

x ≤ 1,

f(x) = (1− x)2 , 1 < x ≤ 3,

x , x > 3.

	cos x,	x < 0,
15.3.		0 ≤ x < 3,
	f (x) = x + 1,
	x2 − 6x + 7, x ≥ 3.
	2 cos x,	x ≤ 0,
15.5.		0 < x < 3,
	f (x) = 2 − x,
	x2 − 6x + 10, x ≥ 3.
	1− 2x,	x < 0,
15.7.
	f (x) = 2tgx + 1, 0 ≤ x < π / 4,
		x ≥ π / 4.
	x − 3,
	3sin x, x < 0,
15.9.		0 ≤ x < 2,
	f (x) = 2x2 ,
	x − 3,	x ≥ 2.

		sin x,			x ≤ 0,
15.2.	f (x) =				0 < x < 2,
		2x2 ,
		3x − 2,			x ≥ 2.
		1+ x,			x ≤ 1,
15.4.	f (x) =	(1− x)2			, 1 < x ≤ 3,
		2x + 2,			x > 3.
		sin x,			x < 0,
15.6.			+ 1,		0 ≤ x < 3,
	f (x) = x
		x2 − 3x + 4, x ≥ 3.
		cos x,			x ≤ 0,
15.8.			− x,		0 < x < 3,
	f (x) = 2
			2	− 6x + 8, x ≥ 3.
		x
		1− 2x,			x < 0,
15.10.
	f (x) = 2x2 + 1, 0 ≤ x < 3,
		2x − 3,			x ≥ 3.

54

3cos x,

x ≤ 0,

3cos x,

x < 0,

15.11.

f (x) =

− x,

0 < x < 3,

15.12.

f (x) =

0 ≤ x < 2,

2

2x2 ,

2

− 6x + 8, x ≥ 3.

x

2x + 4, x ≥ 2.

x2 + 1,

x < 0,

− cos x,

x ≤ 0,

15.13.

f (x) =

cos x,

0 ≤ x < π,

15.14.

f (x) =

2 − x,

0 < x < 3,

− π, x ≥ π.

2

− 6x

+ 7, x ≥ 3.

x

x

2sin x , x ≤ 0,

x2 + 1,

x < 0,

15.15.

f (x) =

3x2 ,

0 < x < 1,

15.16.

f (x) =

sin x, 0 ≤ x < π,

3 − 2x, x ≥ 1.

x − π, x ≥ π.

2сosx ,

x ≤ 0,

2 cos x,

x ≤ 0,

15.17.

f (x) =

2

,

0 < x < 1,

15.18.

f (x) =

− x ,

0 < x ≤ 2,

x

2

− 2x, x ≥ 1.

2

− 4x

+ 5, x > 2.

3

x

4sin x,

x ≤ 0

cos x,

x ≤ 0,

15.19.

f (x) =

3 − x,

0 < x ≤ 2,

15.20.

f (x) =

3 − x ,

0 < x ≤ 2,

x2 − 4x + 5, x > 2.

x2 − 4x + 3, x > 2.

cos x,

x ≤ 0,

2 − x,

x ≤ 1,

15.21.

f (x) =

2x2 ,

0 < x < 2,

15.22.

f (x) =

(1− x)2 , 1 < x ≤ 3,

3x + 2, x ≥ 2.

x + 1,

x > 3.

2 cos x , x ≤ 0,

2 cos x,

x ≤ 0,

15.23.

f (x) =

3x2 ,

0 < x < 1,

15.24.

f (x) =

4 − x,

0 < x < 3,

− 2x,

x ≥ 1.

2

− 6x

+ 10, x ≥ 3.

5

x

sin x,

x < 0,

3 − 2x,

x < 0,

15.25.

f (x) =

+ 1,

0 ≤ x < 3,

15.26.

f (x) =

0 ≤ x < 2,

x

2x2 + 1,

2

− 4x + 7, x ≥ 3.

x

4x + 1, x ≥ 2.

sin x,

x ≤ 0,

3sin x,

x < 0,

15.27.

f (x) =

2

− 4, 0 < x < 2,

15.28.

f (x) =

2

− 5, 0 ≤ x < 2,

2x

x

3x − 2, x ≥ 2.

x − 3, x ≥ 2.

x

2

+ 1,

x < 0,

x ≤ 0,

3cos x,

15.29.

f (x) =

sin x + 1, 0 ≤ x < π,

15.30.

f (x) =

3 − x,

0 < x < 3,

− π,

x ≥ π.

2

− 6x

+ 8, x ≥ 3.

x

x

55

			З А Д А Н И Е				№	1	6
	Дано уравнение f (x) = 0. Требуется: 1) графическим методом отделить
	корень этого уравнения; 2) найти этот корень с точностью до 0,1 методом
	деления отрезка пополам.
	16.1.	2x + 5x = 0.		16.2.		х3 + 2х – 7 = 0			16.3.	х – (х + 1)3 = 0.
	16.4.	ln x + 5x = 0.		16.5.		x ln x – 4 = 0.			16.6. х3 + 3х – 7 = 0.
	16.7.	ln x – 6 + 7x = 0.		16.8.		3x + 4x = 0.			16.9. 4x + 2x = 0.
	16.10.	5x + 3x = 0.		16.11.		2x + 2x – 2 = 0.			16.12. ln x + 3x – 2 = 0.
	16.13.	2х + 5х – 3 = 0.		16.14.		ln x + 3x – 1 = 0 16.15.				x ln x – 5 = 0.
	16.16.	2ex – x2 = 0.		16.17.		ln x – 5 + 6x = 0 16.18.				4x + 5x = 0.
	16.19. ex + 3x = 0.			16.20.		4x + 3x = 0.			16.21.	ex + 5x = 0.
	16.22.	3x2 – 7ex = 0.		16.23.		3x + x = 0.			16.24. 2 ln x + 5x = 0.
	16.25.	2x ln x – 7 = 0.		16.26.		х3 + 4х + 1 = 0.			16.27. ln x – 7 + 8x = 0.
	16.28. 2 3x + 7x = 0.			16.29.		3 4x + 7x = 0.			16.30. 2 5x + 7x = 0.
		8 . М Е Т О Д И Ч Е С К И Е У К А З А Н И Я
		К К О Н Т Р О Л Ь Н О Й Р А Б О Т Е № 3
		8 . 1 .	К О М П Л Е К С Н Ы Е Ч И С Л А
	Выражение вида			z = x + iy,		x, y R					(8.1)
	где i – так называемая мнимая единица, называется комплексным числом.
	Мнимая единица (символ) определяется равенствами
			i =	−1		или	i2 = −1				(8.2)
	В дальнейшем комплексные числа будут представляться в различных фор-
	мах. Вид комплексного числа (8.1) называется его алгебраической формой, х
	называется действительной частью, y – мнимой частью комплексного числа.
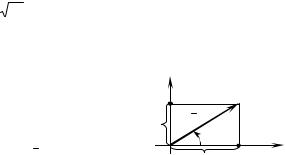
	Комплексное число								y
			z = x − iy								z
	называется сопряженным к числу (8.1).
										r
	Геометрически комплексное число изображает-								y
										ϕ
	ся точкой плоскости с координатами х и y или со-
	ответствующимрадиус-вектором r				(рисунок8.1).				О	x	x
	Действия над комплексными числами вводят-
									Р и с у н о к		8.1
	ся так, чтобы оставались в силе обычные законы
	алгебры и равенства (8.2):

56

1) сложение

(x1 + iy1 ) + (x2 + iy2 ) = (x1 + x2 ) + i( y1 + y2 ),

2)умножение на действительное число λ

λ(x + iy) = λx + i(λy),

3)умножение комплексных чисел

(x1 + iy1)(x2 + iy2 ) = (x1x2 − y1 y2 ) + i(x1 y2 + x2 y1).

4) деление на комплексное число

(x1 x2 + y1 y2 )+ i(x2 y1 − x1 y2 )

x1 + iy1

=

(x1 + iy1 )(x2 − iy2 )

=

=

x2 + iy2

(x2 + iy2 )(x2 − iy2 )

x2 2 + y2 2

=

x1x2 + y1y2

+ i

x2 y1 − x1y2

.

x

2 + y 2

x 2

+ y 2

2

2

2

2

Введём понятие модуля

z = r =

x2 + y2

и аргумента arg z = ϕ комплексного числа (рисунок 8.1). Важно помнить,

что

tgϕ = y / x.

Очевидно, что

x = r cosϕ, y = r sin ϕ.

Подставляя эти выражения в (8.1), приходим к тригонометрической форме комплексного числа:

z= r(cos ϕ + i sin ϕ).

Пр и м е р . Написать в тригонометрической форме комплексное число z = 1+ i .

Р е ш е н и е . Найдем модуль и аргумент этого комплексного числа r = 1+ 1 = 2 , tgϕ = 1 .

Отсюда ϕ равно или π / 4 или – 3π / 4, но так как точка, изображающая комплексное число, попадает, как нетрудно видеть, в первую четверть, то ϕ = π / 4. Тогда

z = 1+ i =		π	+ i sin	π
	2 cos	4		4	. v

При умножении комплексных чисел их модули перемножаются, а аргу-

менты складываются:	[cos(ϕ1 + ϕ2 ) + isin(ϕ1 + ϕ2 )]
z1z2 = r1 r2

z1 z2 = r1 r2 , arg(z1 z2 ) = arg z1 + arg z2.

((8.3)

При делении картина аналогичная

57

	z1	=	r1		[cos(ϕ − ϕ	2	) + isin(ϕ − ϕ	2	)].	(8.4)
	z2		r2		1		1
Если z = r(cos ϕ + i sin ϕ) , то
		zn = rn (cos nϕ + isin nϕ) .								(8.5)

Если n N , то корень n-ой степени из комплексного числа z имеет n различных значений, которые находятся по формуле Муавра

n	z =	n		ϕ + 2πk	+ i sin	ϕ + 2πk		k = 0, n − 1.	(8.6)
			r cos	n		n	,

8 . 2 . В В Е Д Е Н И Е В М А Т Е М А Т И Ч Е С К И Й А Н А Л И З

Функцией называется правило (закон), по которому каждому элементу х (аргументу) некоторого множества Х (области определения) соответствует единственный элемент у (зависимая переменная) другого множества Y (области значения функции).

Множество пар чисел {(x, y) R2 ; x X , y = f (x)} называется графиком

функции y = f (x). Оно определяет некоторую кривую в декартовой системе координат Оху.

Графики функций в прямоугольной системе координат обладают следующими свойствами:

1)график функции y = –f (x) симметричен графику функции y = f (x) относительно оси Ох;

2)график функции y = f (–x) симметричен графику функции y = f (x) относительно оси Оу;

3)график функции y = f (x – a) представляет собой сдвинутый вдоль оси Ох на величину а график y = f (x);

4)график функции y = f (x) + b представляет собой сдвинутый вдоль оси Оy на величину b график y = f (x);

5) график функции y = kf (x) есть растяжение (k > 1) графикa y = f (x) в

kраз (или сжатие при k < 1 в 1 / k раз) вдоль оси Оу;

6)график функции y = f (аx) представляет собой растяжение при а < 1 графикафункции y = f (x) в1 / араз (илисжатие при а> 1 вараз) вдольосиОх.

Число y0 называется пределом функции y = f (x) в точке x0 R (при x → x0), если для любого ε > 0 можно указать такое число δ = δ(ε) , что при всех x X , удовлетворяющих условию 0 < x − x0 < δ , выполняется неравенство

f (x) − y0 < ε .

Аналогично введенным определениям дается и определение предела функции при x → ∞ и бесконечного предела функции в точке.

Наряду с введенным понятием предела функции в точке часто используют понятие одностороннего предела.

58

Число y0 называют пределом функции y = f (x) в точке x0 справа (слева),

если для любого ε > 0 существует такое число δ = δ(ε) , что при всех x X ,

удовлетворяющих условию 0 < x − x0 < δ					(−δ < x − x0 < 0) , выполняется
неравенство		f (x) − y0		< ε .

При вычислении пределов используют следующие символические равенства и формулы:

1

= ∞,

1

= 0,

0

∞

lim C = C ,

lim [f (x) + g(x)]= lim f (x) + lim g(x) ,

x→ x0

x→ x0

x→ x0

x

→ x0

lim [f (x)g(x)]

f (x)

lim f (x)

= lim

f (x) lim g(x) , lim

=

x→ x0

,

g(x)

lim g(x)

x→ x0

x→ x0

x→ x0

x→ x0

x→ x0

lim

sin x

= 1 (первый замечательный предел),

x→0

x

1

x

lim 1

+

= e

(второй замечательный предел).

x

x→∞

Функция y = f (x) называется непрерывной в точке х0, если она определена в некоторой ее окрестности и имеет в этой точке конечный предел, причем

lim f (x) = f (x0 ) .

x→ x0

Здесь не указано, с какой стороны х → x0. Понимают это равенство так
lim	f (x) = lim f (x) = f (x0 ),	(8.7)
x→ x0 −0	x→ x0 +0
Здесь через lim f (x),	lim f (x) обозначены соответственно правый и
x→ x0 +0	x→ x0 −0

левый пределы функции y = f (x) в точке x0.

Если хотя бы одно из равенств в (8.6) не имеет места, функция называется

разрывной, а разность

s(x0 ) = f (x0 + 0) − f (x0 − 0)
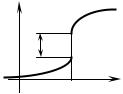
называется скачком функции в точке x0 (см. рисунок	y
8.2).
Точка х0 называется точкой разрыва первого ро-
да функции у = f (х), если f (х) определена в некото-
			s0
рой окрестности точки х0, имеет в ней конечные од-
носторонние пределы f (х0 – 0) и f (х0 + 0), но f (х0 +
0) ≠ f (х0 – 0).	0				x0
								x
Точка х0 называется точкой разрыва второго ро-		Р и с у н о к					8.2

да, если один из односторонних пределов не существует или бесконечен. Заметим, что для точек разрыва первого рода скачок s(х0) функции в точке х0 конечен, а для точек разрыва второго рода – бесконечен.

59

Справедливо утверждение: основные элементарные функции непрерывны

во всех точках области определения.
При решении нелинейных уравнений
f (x) = 0	(8.8)

часто используют приближенные методы.

Рассмотрим метод половинного деления (метод бисекций) численного ре-

шения (8.8).

	Т е о р е м а 8 . 1 . Если функция				y = f (x)		непрерывна на отрезке
[a,b],	принимает значения разных знаков на концах отрезка [a,b]								и первая
производная		f ′(x)	сохраняет знак на интервале			(a,b),		то внутри отрезка
[a,b] существует			единственный	корень ξ	уравнения			f (x) = 0 ,	ξ (a, b)
(рисунок 8.3).p
	y	f ′(x) > 0 x (a, b)			y	y = f (x)
		a	ξ				ξ	x1	b
	0		b	x	0	a	x		x
			f (x)
		Р ис у нок 8.3			Р ис у нок 8.4

Таким образом, при нахождении корней вначале необходимо разбить область определения функции на отрезки, внутри которых находится один корень уравнения (8.8).

Отрезок, содержащий корень, можно найти графически. Для этого

уравнение f (x) = 0 переписывается ввиде

ϕ(x) = ψ(x),

где ϕ(x) и ψ(x) более простые функции, чем f (x) . Построив графики функций y1 = ϕ(x) и y2 = ψ(x) , находим отрезок, содержащий значение ξ

(абсциссу точки пересечения этих графиков), есликорень существует. Рассмотрим один из таких отрезков [a,b], на концах которого функция f (x)

имеет разные знаки (рисунок 8.4). Значение корня ξ находится внутри отрезка [a,b]. Разделим отрезок [a,b] пополам и вычислим значения функции f (x) в

точке х1 = (а + b) / 2.

Если f (x1 ) = 0 , то x1 является корнем уравнения (8.8). Если f (x1 ) ≠ 0 , то выбираем ту из половин [a, x1 ] или [x1, b], на концах которых функция f (x)

имеет противоположные знаки. В рассматриваемом случае (см. рисунок 8.4) это будет отрезок [a, x1 ], который принимаем за новый отрезок. Обозначим этот

60