2298 ЭИ

отрезок через [a1, b1 ]. Если b1 − a1 < ε , где ε – заданная точность, то любая точка из интервала (а1, b1) может быть принята за приближенное значение корня. Если же b1 − a1 ≥ ε , то, положив а = а1, b = b1, продолжаем процесс

деления отрезка пополам. В результате на каком-то конечном шаге получается либо точное значение корня, либо через конечное число шагов длина [an , bn ] станет меньше ε. В последнем случае за приближенное значение

корня можно принять любую точку отрезка [an , bn ] (как правило, берут его середину).

						9 . Р Е Ш Е Н И Е Т И П О В О Г О В А Р И А Н Т А
						К О Н Т Р О Л Ь Н О Й Р А Б О Т Ы № 3
		2			З а д а н и е 1 1 . Даны комплексные числа z1 = −3 + 4i и
	z2	=		29		. а). Записать их в тригонометрической форме и отметить получен-
			5	+ 2i

ные числа на комплексной плоскости; б). Найти числа z1 + z2, z1 – z2, построить; в). Найти z1 z2, z1 / z2, записать в тригонометрической и алгебраиче-

ской формах, сравнить результаты; г). Найти z13 ; д). Найти 3 z2 , построить.

Ре ш е н и е . а). Преобразуем число z2 к виду (8.1), для этого умножим

иразделим его на число, сопряженное к знаменателю

z2 =

29

=

29(5 − 2i)

=

29(5 − 2i)

= 5 − 2i .

5 + 2i

(5 + 2i)(5 − 2i)

25 − 4i2

Запишем числа

z1

и

z2

в тригонометрической форме. Воспользуемся

формулами

z = r = x2 + y2 , tgϕ = y / x,

y

, если z находится в I и IV четверти,

arctg

x

y

+ π, если z

ϕ = arctg

находится в II четверти,

x

y

− π,если z

arctg

находится в III четверти.

x

r = (−3)

2 + 42 = 25 = 5 , tgϕ = −4 / 3.

1

1

Точка z1 попадает во вторую четверть, поэтому ϕ1 = arctg (–4 / 3) + 180°
= = –53,13° + 180° = 126,87° z1 = −3 + 4i = 5 (cos126,87° + i sin126,87°).
r = 52 + (−2)2 =	29 ≈ 5,39 , tgϕ	2	= −2 / 5.
2
	61

Точка z2 попадает в четвертую четверть, поэтому ϕ2 = arctg (–2 / 5) = –

21,8° и

z2 = 5 − 2i = 5,39 (cos(−21,8°) + i sin(−21,8°)).

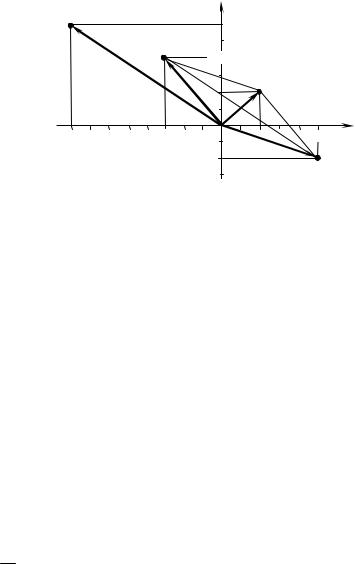
Отметим полученные числа на комплексной плоскости (рисунок 9.1).

							y
z4							6
				z1			5
							4
							2
							1
–8	–7	–6	–5 –4	–3	–2	–1	0
						–1
						–2
						–3
				Р и с у н о к

3

z3

4

1 2 3

5

х

z2

9.1

б). Вычислим z3 = z1

+ z2, z4 = z1 – z2. В алгебраической форме

z3 = z1 + z2 = −3 + 4i + 5 − 2i = 2 + 2i ;

z4 = z1 – z2 = −3 + 4i − (5 − 2i) = −8 + 6i .

Отметим полученные числа на комплексной плоскости (рисунок 9.1).

в). Вычислим z1z2 и z1 / z2.

В алгебраической форме

z z

2

= (−3 + 4i) (5 − 2i) = −15 + 20i + 6i − 8i2 = −7 + 26i ;

1

z

− 3 + 4i

− 3 + 4i

5 + 2i

−15 + 20i − 6i + 8i2

−23 + 14i

1

=

=

=

=

= −0,79

+ 0,48i ;

z2

5

− 2i

5 − 2i

5 + 2i

52 − 22 i2

29

в тригонометрической форме по формулам (8.3), (8.4) имеем

z1

z2 = 5 (cos126,87° + i sin126,87°)5,39 (cos(−21,8°) + i sin(−21,8°))=

= 26,95 (cos105,07°) + i sin105,07°) ,

z1

5(cos126,87° + i sin126,87°)

=

= 0,93(cos148,67° + i sin148,67°).

z2

5,39(cos(−21,8°) + i sin(−21,8°))

Для проверки полученных результатов перейдем от тригонометрической

формы записи комлексных чисел опять к алгебраической:

z1 z2 = 26,95

(cos105,07°) + i sin105,07°) = 26,95

(–0,26 +

0,966i) =

–7,01 +

26,02i,

z1 = 0,93(cos148,67° + i sin148,67°)= 0,93 (–0,854 + 0,52i) = –0,79 + 0,48i. z2

Таким образом, расчеты выполнены верно. 62

в) Вычислим z13 . По формуле (8.5) имеем

z13 = 53 (cos(3126,87°) + i sin(3126,87°)) = 125(cos 380,61° + i sin 380,61°) = = 125(cos 0,61° + i sin 0,61°).

Для нахождения корней третьей степени воспользуемся формулой Муавра

(8.6):

3

z =

3

ϕ + 2πk

+ i sin

ϕ + 2πk

r cos

3

3

, k = 0, 1, 2

3 z2 = 3

− 21,8° + 360°k

+ i sin

− 21,8° + 360°k

=

5,39 cos

3

3

= 1,75(cos(−7,27° + 120°k) + i sin(−7,27° + 120°k)),

k =

0, 2

k = 0 w0 = 1,75(cos(−7,27°) + i sin(−7,27°)) = 1,75(0,99 − 0,13i) = 1,73 − 0,23i

;

k = 1 w1 = 1,75(cos112,73° + i sin112,73°) = 1,75(− 0,39 + 0,92i) = −0,68 + 1,61i ;

k = 2 w2 = 1,75(cos 232,73° + i sin 232,73°) = 1,75(− 0,61− 0,8i) = −1,06 −1,39i .

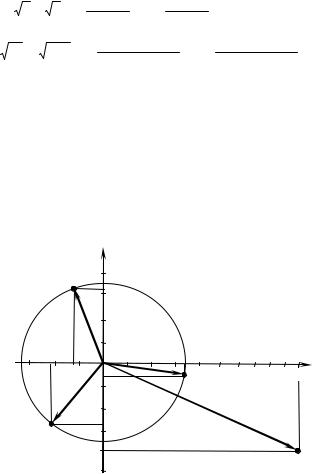
Отметим полученные числа на комплексной плоскости (рисунок 9.2).

	y
w1	2
	1,5
	1,0
	0,5
–1,5 –1	0,5 1	1,5			х
–0,5	0	w02	3	4	5
	–0,5
	–1,0
w2	–1,5

–2,0	z2
–2,5
Р и с у н о к	9.2

2 З а д а н и е 1 2 Методом деформации и сдвигов построить графики функций а) у = 2 sin (2x + π / 3); б) у = 2х – 1 + 4.

63

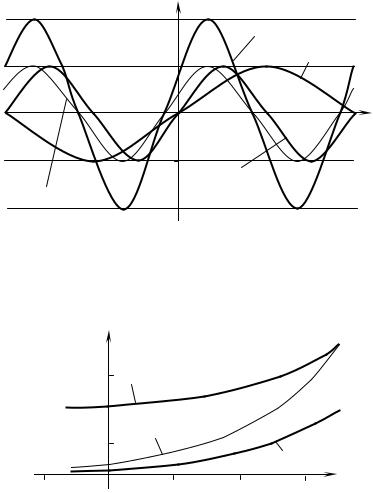
Р е ш е н и е . а). Преобразуем данную функцию к виду у = 2 sin 2(x + π / 6). График функции у = 2 sin 2(x + π / 6) строим следующим образом.

1.Строим график у = sin х.

2.Сжимаем полученный график в 2 раза вдоль оси Ох и получаем гра-

фик у = sin 2х.

3.Сдвигаем график у = sin 2х влево на π / 6 и получаем график у = sin 2(x + π / 6).

4.Растягиваем график у = sin (2x + π / 3) в 2 раза вдоль оси Оу и получаем требуемый график (рисунок 9.3).

у

1

у = 2sin (2x + π / 3)

у = sin x

0,5

–π / 2

π / 2

–π / 6

0

–π

π х

–0,5

у = sin 2x

у = sin (2x + π / 3)

–1

Р и с у н о к

9.3

б). График функции у = 2х – 1 + 4 строим следующим образом.

1.Строим график у = 2х.

2.Сдвигаем график у = 2х вправо на 1 единицу и получаем график у = 2х – 1.

3.Сдвигаем график у = 2х – 1 вверх на 4 единицы и получаем график функ-

ции у = 2х – 1 + 4 (рисунок 9.4). v

у

					6
								у = 2х – 1 + 4
			4
								у = 2х
					2									у = 2х – 1
				0
	–1								1				2				х
															3
								Р и с у н о к				9.4

64

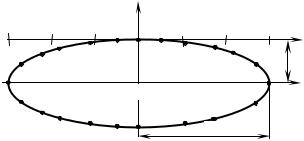
2З а д а н и е 1 3 . Построить кривую, заданную параметрическими

уравнениями x = 3sin t,	по точкам, придавая t значения от t = 0 до t =
y = cost −1
2π c шагом π / 10.

Преобразовать уравнения к уравнениям линии в декартовой системе координат. Определить вид и параметры кривой.

Р е ш е н и е . Для построения кривой заполним таблицу 7.

Таблица 7

t (рад.)		sin x	cos x	x	y	t (рад.)		sin x	cos x	x	y
0		0	1	0	0	π		0	–1	0	–2
π / 10		0,309	0,951	0,927	–0,049	11π /	10	–0,309	–0,951	–0,927	–1,951
π /	5	0,588	0,809	1,763	–0,191	6π /	5	–0,588	–0,809	–1,763	–1,809
3π /	10	0,809	0,588	2,427	–0,412	13π /	10	–0,809	–0,588	–2,427	–1,588
2π / 5		0,951	0,309	2,853	–0,691	7π /	5	–0,951	–0,309	–2,853	–1,309
π /	2	1	0	3	–1	15π /	10	–1	0	–3	–1
3π / 5		0,951	–0,309	2,853	–1,309	8π /	5	–0,951	0,309	–2,853	–0,691
7π /	10	0,809	–0,588	2,427	–1,588	17π /	10	–0,809	0,588	–2,427	–0,412
4π / 5		0,588	–0,809	1,763	–1,809	9π /	5	–0,588	0,809	–1,763	–0,191
9π /	10	0,309	–0,951	0,927	–1,951	19π /	10	–0,309	0,951	–0,927	–0,049
						2π		0	1	0	0

Используя данные таблицы, построим кривую (рисунок 9.5).

			у, у′
–3	–2	–1	1	2	3
			O		х
					b = 3
			–1
			O′(0, –1)		х ′

–2 а = 3

Р и с у н о к 9.5

Исключим из параметрических уравнений параметр t и получим уравнение, содержащее только х и у. Возводя в квадрат параметрические уравнения

и складывая, находим

х2 + у2 = 9 sin2 t + cos2 t – 2 cos t + 1; х2 + у2 = 9(1 – cos2 t) + cos2 t – 2 cos t + 1;

х2 + у2 = 9 – 8 cos2 t – 2 cos t + 1;

х2 + у2 = 10 – 8 cos2 t – 2 cos t. (9.1)

Выразим cos x из второго уравнения параметрически заданной линии cos x = у + 1

65

и подставим в (9.1)

х2 + у2 = 10 – 8 (у + 1)2 – 2 (у + 1).

Произведя необходимые преобразования, получим

х2 + у2 = 10 – 8у2 – 16у – 8 – 2у – 2 х2 + 9у2 + 18у = 0 х2 + 9(у2 + 2у + 1) = 9

2		2			х2		( у+ 1)	2
х	+ 9(у + 1)		= 9			+			= 1 .
					33		1

Получили уравнение эллипса с центром в точке О′(0, –1) и полуосями а = 3, b = 1, что соответствует рисунку 9.5. v

2 З а д а н и е 1 4 . Вычислить пределы

а) lim

x→ x0

б) lim

x→1

3x2 − x	− 2	при х0		= 2; х0 = 1; х0 → ∞.
2x2 + x − 3
										3x+1
x + 3 −	5 − x				1− cos x			2x − 1
			; в)	lim		; г)	lim				.
x −1				x→0	sin2 x		x→∞	2x + 1

Р е ш е н и е . При вычислении пределов допустимы использование уже известных пределов и элементарные преобразования. В некоторых случаях бывает целесообразным использовать для приближенных вычислений при малых значениях х (всюду х → 0 ) таблицу эквивалентных бесконечно малых:

1)

sin x х,

2) tg x х,

3) arcsin x х,

4)

arctg x х,

5) 1− cos x

x2 / 2 ,

6) ln(1+ x) х,

7) ex −1 х,

8) ax − 1 х ln a,

9) (1+ x)a − 1 aх.

3x2 − x − 2

3 22 − 2 − 2

8

а)

1.

lim

= lim

=

;

2x2 + x − 3

2 22 + 2 − 3

7

x→2

x→2

3x2 − x − 2

0

а)

2.

lim

=

.

2x

2

+ x − 3

x→1

0

Неопределенности вида 0 раскрываются путем сокращения намножитель,0

дающий 0. Разложим числитель и знаменатель на множители по формуле

ax2 + bx + c = a(x − x )(x − x	2	) . Для этого решим уравнения 3x2	− x − 2 = 0 и
1

2x2 + x − 3 = 0 . Корнипервогоуравнения– {1, –2 / 3}, второго– {1, –3 / 2}, тогда

3x2

− x − 2 = 3(x − 1)(x + 2 / 3) ,

2x2

+ x − 3 = 2(x − 1)(x + 3 / 2) .

Подставим полученные разложения под знак предела и получим

3x2 − x − 2

0

3(x −1)(x + 2

/ 3)

3(x + 2 / 3)

=

5

= 1.

lim

=

= lim

= lim

2x

2

+ x − 3

0

2(x − 1)(x + 3

/ 2)

2(x + 3 / 2)

5

x→1

x→1

x→1

66

а) 3.		3x2 − x − 2				∞
	lim				=	.
			2	+ x − 3
	x→∞ 2x					∞

Такие неопределенности раскрываются путем вынесения старшей степени неизвестной

2

1

2

1

2

3x2 − x − 2

x

3

−

−

3

−

−

x

x2

3

lim

= lim

= lim

x

x2

=

.

1

3

1

3

2

x→∞ 2x2 + x − 3

x→∞

2

x→∞

2

+

−

x

2

+

−

x

x2

x

x2

lim

x + 3 − 5 − x

= 0

.

б)

x→1

x −1

0

Для того, чтобы избавиться от иррациональностей, умножим и числитель и знаменатель на выражение, сопряженное числителю:

lim

x + 3 −

5 − x

= lim ( x + 3 − 5 − x )

(

x + 3 +

5 − x )

=

x −1

x + 3 + 5 − x )

x→1

x→1

(x −1)

(

= lim

(x + 3) − (5 − x)

= lim

2(x −1)

=

x + 3 +

5 − x )

x→1 (x −1)( x + 3 + 5 − x )

x→1 (x − 1)(

= lim

2

=

2

=

1

.

( x + 3 +

5 − x )

2 + 2

x→1

2

в)

1− cos x

0

lim

=

.

sin

2

x

x→0

0

Для раскрытия неопределенностей такого вида воспользуемся первым за-

мечательным пределом lim

sin x

= 1

и равенством 1− cos x = 2sin

2

x

. Тогда

x→0

x

2

2 x

2 x

x

2

1− cos x

2sin

sin

x2

2

lim

= lim

2

= 2 lim

2

=

sin2 x

sin2 x

x2

x→0

x

→0 sin2 x

x→0 x 2

2

2 x

x

2

x

2

sin

x2

2

2

1

= 2 lim

2

lim

lim

= 2 lim

=

.

x2

x2

2

x→0 x 2

x

→0 sin2 x

x→0

x

→0

2

2x − 1 3x+1

∞

г)

lim

= [1

] .

x→∞

2x + 1

67

Для раскрытия неопределенностей вида [1∞ ] воспользуемся вторым заме-

1 x

чательным пределом

lim 1+

= e.

Тогда

x→∞

x

3x+1

3x+1

2x − 1

2x −1

lim

= lim 1+

−1

=

2x + 1

x→∞ 2x + 1

x→∞

−2

2x+1

(3x+1)

2x

− 1− 2x − 1

3x+1

−

2

2x+1

−2

= lim 1

+

= lim

1+

=

2x + 1

2x

x→∞

x→∞

+ 1

−6x−2

x(−6−2 / x)

−6−2 / x

= lim e 2x+1 = lim e

x(2+1/ x)

= lim e

= e−3 . v

2+1/ x

x→∞

x→∞

x→∞

x2 , x

≤ 0,

2 З а д а н и е

1 5 .

Задана функция f (x) =

0 < x < 2, Уста-

2x − 1,

5 − x,

x ≥ 2.

новить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.

Р е ш е н и е . В интервалах (–∞; 0), (0, 2) и (2, ∞) функция непрерывна. Исследуем функцию на непрерывность в точках х1 = 0 и х2 = 2. Воспользуемся условием непрерывности функции в точке х0 (8.6)

1)	исследуем точку х1 = 0:			lim f (x) = lim (2х−1) = −1
	lim	f (x) = lim x2 = 0;
	x→0−0	x→−0		x→0+0	x→+0
		lim	f (x) ≠ lim		f (х)
		x→0−0		x→0+0	1 рода со cкачком s(0) = –1;
точка	х1 = 0 – точка разрыва			функции
2)	исследуем точку х2 = 2:
		lim	f (x) = lim(2x −1) = 3;
		x→2−0		x→2

68

lim	f (x) = lim(5 − x) = 3; f (2)= 3 ,
x→2+0	x→2

следовательно, в точке х2 = 2 функция непрерывна. Построим график (см. рисунок 9.6). v

у

			4
y = x2			3				y = 5 – x
			2
			1	y = 2x – 1
–3	–2	–1	0	1	2	3	4	х
		–1
		Р и с у н о к				9.6
2 З а д а н и е 1 6 . Дано уравнение							x3 + x − 1 = 0 . Требуется: 1) Гра-

фическим методом отделить корень этого уравнения. 2) Найти этот корень методом половинного деления с точностью ε = 0,1.

Р е ш е н и е . Для нашего примера примем

ϕ(x) = x3 ; ψ(x) = 1− x .

Графики этих функцийизображены нарисунке 9.7.

y

3

y = x3

y = 1 – х

2

1

0

–2

–1

ξ 1

2 x

–1

Р и с у н о к

9.7

Как видно, ξ [0, 1]. Рассмотрим отрезок [0, 1]. Имеем

f (0) = −1 < 0 ; f (1) = 1 > 0 ; f ′(x) = 3x + 1 > 0 x [0, 1].

Таким образом, на отрезке [0, 1] функция f (x) удовлетворяет условиям теоремы 8.1 и на этом отрезке имеет единственный корень. Рассмотрим интервалы (− ∞;0) и (1;∞):

f (x) < 0 x (− ∞;0); f (x) > 0 x (1;∞),

т. е. на этих интервалах функция f (x) не меняет знак, следовательно, корней на них нет.

69

Найдем корень на отрезке [0, 1]. Итерационная процедура метода

половинного деления будет иметь вид

ξ [0, 1],

0

+ 1

3

1)

f

= f (0,5) = 0,5

+ 0,5 −1 = −0,375 < 0;

2

ξ [0,5; 1],

0,5 + 1

3

2)

f

=

f (0,75)

= 0,75

+ 0,75 – 1 = 0,172 > 0;

2

ξ [0,5; 0,75],

0,5 + 0,75

3

3)

f

= f (0,625) = 0,625

+ 0,625 – 1 = –0,131 < 0;

2

ξ [0,625; 0,75],

0,625 + 0,75

3

4)

f

= f (0,688) = 0,688

+ 0,688 – 1 = 0,012

2

>0;

5)ξ [0,625; 0,688].

Так как длина последнего отрезка 0,688 − 0,625 = 0,063 < ε = 0,1, то процесс закончен и приближенное значение корня ξ [0,625; 0,688]. Возьмем в качестве корня середину отрезка, т. е. ξ ≈ 0,66.

Для проверки результатов расчетов вычислим f (0,66): f (0,66) ≈ −0,053 , т. е. корень найден верно. v

Б И Б Л И О Г Р А Ф И Ч Е С К И Й С П И С О К

1.Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.:

Наука, 2004. 376 с.

2.Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. для втузов. В 2-х томах. Т. I. М.: Интеграл-пресс, 2007. 416 с.

3.Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упраж-

нениях и задачах. Часть 1. М.: Высшая школа, 2007. 416 с.

4.Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая матема-

тика для экономических специальностей: Учебник и практикум. Ч. 1. Под ред. Кремера Н.Ш. М.: Высшее образование, 2005. 486 с.

5.Письменный Д.Т. Конспект лекций по высшей математике (часть 1). М.: Айрис-пресс, 2004. 288 с.

6.Берман Г.Н. Сборник задач по курсу математического анализа. СПб.: Про-

фессия, 2008. 432 с.

7.Клетеник Д.В. Сборник задач по аналитической геометрии. СПб.: Профес-

сия, 2007. 200 с.

8.Высшая математика: Методические указания, рабочая программа и контрольные задания для студентов заочной формы обучения инженернотехнических специальностей. Часть 1 // Ю.В. Гуменникова, Л.В. Кайдалова, А.В. Ефашкин, Н.Н. Щипкова; Самара: СамГАПС. 2005. 74 с.

70