2253 ЭИ

№

З А Д А Н И Е

Р Е Ш Е Н И Е

С(0, –2), СD – его медиана.

ка АВ):

хd =

ха + хb

=

3 − 3

= 0 ,

Тогда координаты

точки

D

2

равны …

yа + yb

2

yd =

=

4 + 4

= 4 D (0, 4).

2

2

Если

а

= 1,

= 2

и угол

a

cos(a,

),

b

b

=

a

b

b

между векторами a

и

ра-

a

= a(а +

) = a 2 + а

=

b

23.

c

b

b

вен π / 3, то скалярное произ-

2

ведение

векторов

a

и

=

a

+

a

b

cos (a,b) = 12 + 1 2 сos (π / 3)

c = a +

равно …

= 1 + 2 (1 / 2) = 2.

b

Векторы

=

(3,

2k,

5)

и

Условие перпендикулярности

a

24.

= (–3, 1, 2) перпендикуляр-

a

b

= 0

axbx + ayby + azbz = 0

b

ны, если k = …

3(–3) + 2k + 5 2 = 0 k = –0,5.

Условие коллинеарности

a

x

a y

a

z

а× b = θ

=

=

Векторы

a = (3,

2α, 5) и

bx

by

25.

bz

b

= (–3,

1,

β)

коллинеарны,

3

=

2α

=

5

.

если α = …, β = …

− 3

1

β

Значение каждой из дробей равно –1

α = –0,5; β = –5.

Известно, что

а

= 7,

=

Учитывая свойство скалярного произ-

b

ведения a b

a b = 0 , находим

5, a

.

Тогда

значение

26.

b

(4

− a)

= 4

− a

= 4(

)2 =

b

b

b

b

b

b

скалярного

произведения

2 = 100 .

(4

− a)

равно…

= 4

b

b

b

Для векторов а = (1, 0, − 3) и

Найдем скалярное произведение a

.

b

= (− 6, 1, − 2)

справедливы

Если

a

= 0

векторы

перпендику-

b

b

утверждения …

лярны, если a

< 0 угол между век-

b

1) Векторы

a

и

b

не пер-

торами

тупой,

если

a

> 0

угол

27.

пендикулярны.

b

острый.

2) Вектор a

перпендикуля-

рен оси Oу.

a

b

= axbx + ayby + azbz

= –6 + 6 = 0

3) Вектор

параллелен оси

векторы перпендикулярны

невер-

b

Oх.

но утверждение 1).

4) Вектор a

образует тупой

Вектор перпендикулярен

оси,

проек-

11

№

З А Д А Н И Е

Р Е Ш Е Н И Е

угол с осью Oz.

ция на которую равна 0 верно утвер-

5) Векторы a и

коллине-

ждение 2).

b

арны.

Вектор параллелен оси,

если он пер-

пендикулярен двум другим осям, т. е.

две соответствующие проекции равны 0

утверждение 3) неверно.

Вектор образует тупой угол с той

осью, проекция на которую отрицатель-

на утверждение 4) верно.

Векторы

a

,

если

а×

=

b

b

θ

a

x

=

ay

=

a

z

1

≠

0

≠

−3

век-

b

x

b

y

b

− 6

1

− 2

z

торы неколлинеарны.

Итак, справедливы утверждения 2) и

4).

i

j

×

k

= i

3

− 1

− j

− 2

− 1

Векторное

произведение

a

b

=

− 2

3

− 1

28.

векторов

а = (− 2, 3, − 1) ,

0

1

5

1

5

0

5

=(0, 1, 5) равно …

b

− 2 3

.

+ k

= 16i + 10 j − 2k

0

1

ax

a y

az

Смешанное

произведение

(a

b

c) =

bx

by

bz

,

29.

векторов

а = (−2, 0, 0),

cx

c y

cz

и c = (2, 3, − 1)

b = (3, − 1, 1)

− 2

0

0

−1

1

равно …

= 4 .

(abc) =

3

−1 1

= −2

3 −1

2

3

−1

Объем параллелепипеда, по-

Объем параллелепипеда, построенного

на векторах а,

и

с , определяется по

b

строенного

на

векторах

формуле

30.

а = (λ, 0, 0),

b

= (3,

− 1, 1) ,

ax

ay

az

c = (2, 3, −1) ,

равен 4,

если λ

V =

(ab c)

, (ab c) =

bx

by

bz

.

принимает значения …

cx

cy

cz

12

№

З А Д А Н И Е

Р Е Ш Е Н И Е

(a

c) =

λ

0

0

−1 1

3 −1 1

= 4; λ

= 4;

b

2

3

−1

3

−1

λ(1− 3) = 4 λ = −2 .

Модуль нормированного вектора ра-

В евклидовом пространстве

вен 1. Тогда

3

2

1

2

2

1

2

R

вектор а = λ, −

,

яв-

a =

2

+

= 1

31.

3

3

λ +

−

3

3

ляется нормированным

при

4

1

5

2

значениях λ, равных …

2

2

λ

+ 9 +

9

= 1 λ +

9 = 1 λ = ±

3 .

Для заданного вектора х = (х1,

х2 )

со-

ответствующий

ему

нормированный

х

х

2

Нормированным вектором в

вектор имеет

вид

х0

=

1

,

,

где

х

х

32.

R2 для вектора х = (3, 4)

явля-

ется…

х =

х12 + х22

. Тогда

х =

32 + 42 = 5

3

4

0

х

=

,

.

5

5

Норма вектора

а = (х1, х2 , х3, х4 )

оп-

Значение х < 0, при котором

ределяется равенством

а

=

х2

+ х2

+ х2 + х2

33.

норма вектора а = (1, 3,

х, − 1)

1

2

3

4

12 + 32 + х2 + (−1)2

= 6 х2 = 25.

равна 6, равно…

Откуда x = –5 (x = 5 не удовлетворяет

условию х < 0).

Два вектора в R4 линейно зависимы

тогда и только тогда, когда координаты

Векторы а = (х, 10, –4, 12),

их пропорциональны, т. е.

34.

= (3, 5, у, 6) линейно зави-

х

10

−4

12

b

=

=

=

.

симы при х = …, у = …

3

5

у

6

Значение каждой из дробей равно 2,

отсюда находим x = 6, y = –2.

13

№	З А Д А Н И Е	Р Е Ш Е Н И Е
		Нормальный вектор		плоскости
	Нормальный вектор плоско-					n
		имеет координатами коэффициенты при
35.	сти	x, y, z в общем уравнении плоскости
	х + 2у + z – 15 = 0	Ах + By + Cz + D = 0
	имеет координаты…
		n = ( A, B,C)	n = (1, 2, 1) .
	Из уравнений	Уравнение плоскости		Ах + By + Cz +
	а) 2x – 3y + z + 1 = 0;
	б) x + 2y – 6 = 0;	D = 0, параллельной оси Oz, имеет ко-
36.	в) x + 3y = 0	эффициент при	z	равный 0
	выберите те, которые опреде-	C = 0 Ax + By + D = 0 случаи б) и
	ляют плоскость, параллель- в).
	ную оси Oz.
	Уравнение	Данная плоскость пересекает все ко-
	3х + у – 2z – 6 = 0

37.определяет плоскость, пересе- ординатные плоскости (Oxy, Oxz, Oyz), кающую координатные плос- так как в ее уравнении отличны от нуля кости … все коэффициенты при х, у и z.

Какая точка лежит в плоско-

Координаты точки, лежащей на плос-

сти

кости, должны тождественно удовлетво-

2х + у – 3z + 4 = 0

рять этому уравнению:

38.

1) 2 0 + 0 – 3 0 + 4 ≠ 0;

из перечисленных?

2) 2 (–2) + 0 – 3 0 + 4 = 0;

1) (0, 0, 0);

2) (–2, 0, 0);

3) 2 5 + (–1) – 3 7 + 4 ≠ 0;

3) (5, –1, 7);

4) (4, –1, 1).

4) 2 4 + (–1) – 3 1 + 4 ≠ 0 2).

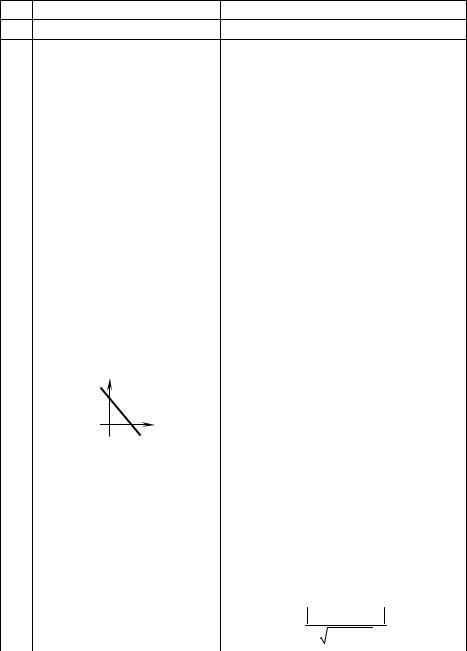
1 способ. Уравнение прямой у = kx +

b. Точки (0, 2) и (–1, 0) принадлежат

прямой

Уравнение линии на рисунке

b = 2,

b = 2, k = 2 у = 2х + 2.

имеет вид…

− k + b = 0

y

2 способ. Уравнение прямой, прохо-

39.

дящей через две точки (х1, у1) и (х2, у2),

2

имеет вид

x − x1

=

y − y1

− x

x

2

y

2

− y

–1

0 x

1

1

x + 1

=

y − 0

y = 2x + 2.

0 + 1

2 − 0

3 способ. Уравнение прямой в отрез-

ках имеет вид

х

+

y

= 1

х

+

y

= 1

а

b

−1

2

14

№

З А Д А Н И Е

Р Е Ш Е Н И Е

y= 2x + 2.

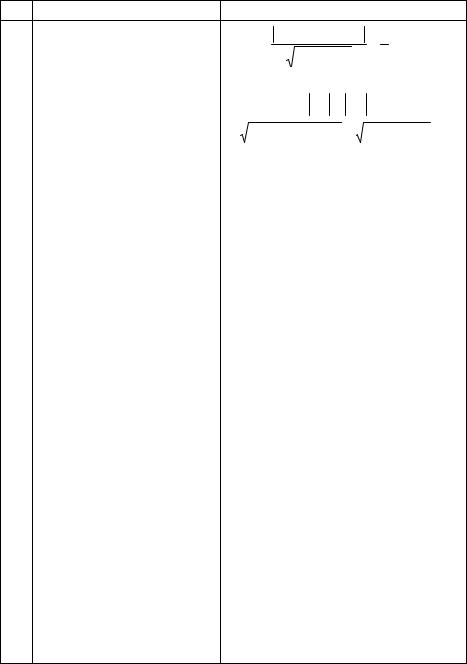
1способ. Прямая проходит через начало координат, следовательно, ее уравнение имеет вид у = kx, откуда k = у / х. Так как точка В принадлежит прямой, то

Прямая проходит через точ-

k = –1 / 2.

2 способ. Составим каноническое

40. ки О(0, 0) и В(–2, 1). Тогда ее

угловой коэффициент равен…

уравнение прямой, проходящей через

точки О(х1, у1) и В(x2, y2):

х− х1

=

у− у1

х− 0

=

у− 0

х

2

− х

у

2

− у

− 2 − 0

1− 0

1

1

у = –х / 2 k = –1 / 2.

1 способ.

По условиям

задачи

А ≠ 0,

В ≠ 0, С ≠ 0. Прямая проходит через точ-

График прямой линии, за-

ки

(0,

1)

и (1,

0)

В+ С = 0,

А+ С = 0

данной уравнением

В = А=

Ах + Ву + С = 0,

– С справедливы утвер-

ждения 1) и 3).

имеет вид…

2 способ. Преобразуем общее уравне-

ние прямой

Ах + Ву + С = 0

41.

у

к виду

x

+

y

= 1

. Введем обо-

1

− C / A

− C / B

0

1 х

значения a = − C

, b = − C

x

+

y

= 1

Правильными

утверждениями

A

B

a

b

– уравнение прямой в отрезках. В дан-

являются…

C

ном случае а = 1 и b = 1 −

= 1,

1) АВ > 0;

2) BC > 0;

A

3) BC < 0;

4) AB < 0.

−

C

= 1 A = B = –C АВ > 0; BC < 0,

B

т. е. справедливы утверждения 1) и 3).

Расстояние от точки М(1, 2)

Расстояние от точки М(х0, у0) до пря-

до прямой

мой Ах + Ву + С = 0 определяется по

42.

4у = 3х + 10

формуле

Ax0 + By0 + C

d =

равно…

A2 + B2

15

№

З А Д А Н И Е

Р Е Ш Е Н И Е

		d = 31+ (−4) 2 + 10 =							5 = 1 (ед.).
		3	2	+ (−4)		2			5
Треугольник с	вершинами	Из условия		равенства					длин сторон
A(0, 1), B(2, –3),	C(4, k) и ос-	треугольника		AB	=		AC	имеем

43.нованием BC является равно-

бедренным

при

k < 0 рав-

(2 − 0)2 + (3 + 1)2 =

42 + (1− k)2

ном…

4 = (1 – k)2 k1 = 3, k2 = –1 k = –1.

Уравнением прямой, парал-

Условие параллельности двух прямых

лельной у = 2х –1, является …

А1х + В1у + С1 = 0 и А2х + В2у + С2 = 0

44.

1) 2х + у + 1 = 0;

имеет

вид

A1

=

B1

= λ,

λ ≠ 0 R

2) х – у – 2 = 0;

3) х + у – 1 = 0;

A2

B2

4) 2х – у + 3 = 0.

данной прямой параллельна прямая 4).

Уравнение прямой перепишем в кано-

Даны уравнения плоскостей

ническом виде

х− 3

=

у+ 1

=

z

на-

−1

2

3

1) – 3х + 5у – z – 2 = 0;

правляющий

вектор

прямой

2)

– у – 3z + 5 = 0;

s = (2, 3, − 1) . Нормальные векторы для

3)

– х – 3z – 2 = 0;

каждой из плоскостей равны соответст-

45.

4)

– 5х + 3у – z – 3 = 0.

венно

n1 = (−3, 5, − 1) ,

n2 = (0, − 1, − 3) ,

Прямая x = 3 + 2t,

n3 = (−1, 0, − 3) , n4 = (−5, 3, − 1) .

Условие параллельности данной пря-

y = –1 + 3t;

мой и

плоскости

состоит

в

равенстве

z = – t

нулю скалярного произведения n s = 0 .

параллельна плоскости…

Это равенство выполняется только для

плоскостей 2), 4).

2

Образ вектора x =

в ба-

y = Ax

4

46.

зисе

линейного

оператора,

−1

2

2

6

заданного

матрицей

−1

2

y =

− 5

=

.

A =

4

4

−12

, имеет вид…

−

4

5

Если

линейный

оператор в

В

базисе

( е1, е2 )

вектор

47.

х = 1 е

+ 0 е

2

. Тогда образ у = Ах имеет

базисе ( е1, е2 ) задан матрицей

1

вид

16

№

З А Д А Н И Е

Р Е Ш Е Н И Е

2

−1

, то образ у = Ах

Aх =

2

−1

1

2

A =

=

3

3

4

4

0

3

вектора х = е1 имеет вид …

у = (2, 3).

Уравнение

Дополним уравнение до полного квад-

2x2 + 2y2 + x = 0

рата 2(x2 + x / 2 + 1 / 16) + 2y2 = 1 / 8

48.

2(x + 1 / 4)2 + 2y2 = 1 / 8

(x + 1 / 4)2 +

определяет на плоскости…

y2 = 1 / 16

окружность с центром

О(–1 / 4; 0) и радиусом R = 1 / 4.

Уравнение окружности с центром в

точке (х0, у0) и радиусом R имеет вид

Если С(1, 1) – центр окруж-

(х – х0)2 + (у – у0)2 = R2

49.

ности, которая проходит через

(х – 1)2 + (у – 1)2 = R2.

точку

А(5, 4), то уравнение

Точка А(5, 4) принадлежит окружно-

этой окружности имеет вид …

сти, следовательно,

(5 – 1)2 + (4 – 1)2 = R2 R = 5.

Итак, (х – 1)2 + (у – 1)2 = 25.

Кривизна окружности, за-

Для окружности радиуса R кривизна

равна k = 1/ R . Для нахождения радиуса

данной уравнением

окружности

дополним

уравнение до

50.

х2 – 2х + у2 + 2у – 7 = 0,

полного квадрата

(x

2

− 2x

+ 1) + ( y

2

+ 2 y + 1) = 9 ,

равна…

(x − 1)2 + ( y + 1)2 = 9

О(1; –1), R = 3.

Тогда k = 1 / 3.

Если

уравнение гиперболы

x2

y2

имеет вид

(a > 0, b > 0)

2

2

−

= 1

– канониче-

51.

x

−

y

= 1 ,

a2

b2

ское уравнение гиперболы, где а – дей-

4

9

ствительная полуось, b – мнимая полу-

то длина ее действительной

ось а = 2.

полуоси равна…

x2

y2

Уравнение

гиперболического парабо-

Уравнение

z =

+

оп-

x2

y2

52.

2 р

2q

z =

лоида имеет вид

−

. Тогда

ределяет

гиперболический

a2

b2

параболоид, если…

2р > 0, 2q < 0.

53.

Геометрический образ урав-

Приведем

канонические

уравнения

нения

основных поверхностей второго порядка

17

№

З А Д А Н И Е

Р Е Ш Е Н И Е

x2

+

y2

−

z2

= 0

x2

+

y2

+

z2

= 1

–

эллипсоид,

5

6

3

a2

b2

c2

есть…

x2

+

y2

−

z

2

= 1

– однополостный

ги-

a2

b2

c2

перболоид,

x

2

−

y

2

−

z2

= 1 –

двуполо-

a

2

b2

c2

стный гиперболоид,

z =

x2

+

y2

–

эл-

a2

b2

липтический параболоид,

z =

x

2

−

y2

–

a

2

b2

гиперболический

параболоид,

x2

+

y2

= 1 – эллиптический цилиндр,

a2

b2

x2

−

y2

= 1 – гиперболический цилиндр,

a2

b2

y2 = 2 px

– параболический

цилиндр,

x2

+

y2

−

z2

= 0 – конус

в

данном

a2

b2

c2

случае конус, а2 = 5, b2 = 6, c2 = 3.

Если все

λ i > 0 , где λi

– собственные

значения матрицы A квадратичной фор-

мы, то квадратичная форма называется

положительно определенной.

Квадратичная форма

Составим матрицу квадратичной фор-

мы A =

α

− 3

. По критерию Силь-

2

2

5

− 3

54.

α х1 − 6х1х2 + 5х2

вестра для положительно определенной

квадратичной

формы

главные

миноры

является

положительно

опре-

α

− 3

деленной при α равном …

матрицы

1 = α,

2 =

должны

1) –5;

2) 0;

3) 1;

4) 2.

− 3

5

удовлетворять условиям

> 0,

α > 0,

1

α

− 3

> 0

> 0

2

− 3

5

18

№

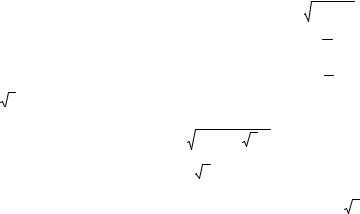
З А Д А Н И Е

Р Е Ш Е Н И Е

α > 9 / 5. Таким образом, в версиях отве-

тов верно только 4).

Составим матрицу квадратичной фор-

мы

α

− 2

Квадратичная форма

A =

− 5

. По критерию Силь-

− 2

αх12 − 4х1х2 − 5х22

вестра в случае отрицательно опреде-

ленной формы главные миноры матрицы

55.

является отрицательно опре-

1 = α, 2 =

α

− 2

должны

удовле-

− 2

− 5

деленной при α равном …

творять условиям

1) 3;

2) 5;

1 < 0,

α < 0,

α < –4 / 5.

> 0

3) –2;

4) –0,5.

2

− 5α − 4 > 0

В версиях ответа этому условию удов-

летворяет только α = –2.

На плоскости введены пря-

Формулы, выражающие декартовы ко-

моугольная и полярная систе-

ординаты точки через полярные, имеют

мы координат, причем поло-

вид

x

= r cos ϕ ,

56.

жительная полуось абсцисс

совпадает с полярной осью.

Если (r, ϕ) – полярные коор-

y

= r sin ϕ .

динаты точки М, то абсцисса

Поэтому х = r cos ϕ.

этой точки равна…

Полярная и декартова системы коор-

динат связаны соотношениями

r =

х2

+ у2 ,

у

x = r cos ϕ ,

sin ϕ =

,

= r sin ϕ ,

r

y

ϕ = x

Полярные координаты точки

cos

,

r

57.

М(–1,

3 ) имеют вид…

r ≥ 0, 0 ≤ ϕ ≤ 2π.

В условиях задания имеем

r =

(−1)2 + (

3)2

= 2 , cos ϕ = –0,5;

3 / 2 ϕ = 2π / 3

2π

sin ϕ =

2,

–

3

полярные координаты точки (–1,

3 ).

19

№

З А Д А Н И Е

Р Е Ш Е Н И Е

Уравнение линии

(r 2 cos 2 ϕ + r 2 sin 2 ϕ)3 = 3r cos ϕ

(х

2

2 3

= 3х

+ у )

58.

в полярных

координатах

r 6 (cos 2ϕ + sin 2 ϕ)3 = 3r cos ϕ

( x = r cos ϕ ,

y = r sin ϕ ) имеет

r 6 = 3r cos ϕ r 5 = 3 cos ϕ .

вид…

Разностью множеств A и B называ-

ется множество, состоящее из всех тех

А и В – множества действи-

элементов

множества

A ,

которые не

тельных чисел:

А = [− 2, 5),

принадлежат множеству B .

59.

В = (0, 8].

Тогда

множество

А

В

А \ В равно…

–2 А \ В0

5

8

х

А \ В = [− 2, 0].

Декарто-

yy

вым

произве-

дением

мно-

А

A × B

жеств

А и

В

называется

b

множество

0

B

Даны множества

всех

упоря-

1

2

3 x

доченных пар

x A ,

A = {b, y} и B = {1, 2, 3}.

элементов

(x, y) ,

в которых

60.

Тогда декартовым (прямым)

y B .

Если А и В – числовые множества, то

произведением A × B являет-

элементами

декартова

произведения

ся…

этих

множеств

будут

упорядоченные

пары чисел. Изображение каждой пары

чисел на плоскости позволяет получить

фигуру на этой плоскости. Таким обра-

зом,

A × B = {(b, 1), (b, 2), (b,3), (y, 1), (y, 2),

(y, 3)}.

Пересечение множеств

Пересечением множеств А и В называ-

А = {1, 3, 5, 10}

ется множество, образованное из всех

61.

и

тех элементов, которые принадлежат и

В = {3, 5, 7}

множеству А, и множеству В

A I B =

равно…

{3, 5}.

20