ФБТ БИ 1курс / физика лекції

2.сила завжди направлена до положення рівноваги.

Розглянемо пружину так, щоб зміщення кульки відносно рівноваги дорівнювало якомусь

значенню a. У цьому стані енергія системи складається із потенціальної енергії, що обумовлена додатковим розтягом пружини. Після цього предоставимо систему самій собі. Під дією сили F кулька рухається з прискоренням до положення рівноваги. При цьому потенціальна енергія пружини перетворюється у кінетичну енергію руху кульки.

В стані рівноваги на кульку не діє ніяка сила, тобто пружина повертається у свій початковий стан.

l = l + l .

Потенціальна енергія розтягу пружини повністю перейшла в кінетичну і тому швидкість кульки стала максимальною. З положення рівноваги кулька буде рухатися вверх, зжимаючи пружину. Внаслідок цього на кульку діє сила F=-kx. Швидкість кульки буде зменшуватись, а її кінетична енергія буде перетворюватись в потенціальну енергію зжимання пружини.

В крайньому верхньому положенні швидкість кульки дорівнює нулю, і кінетична енергія повністю перетворюється в потенціальну енергію пружини.

Якщо на систему не діють ніякі сили, то під дією сили kx кулька буде здійснювати коливання від а до –а. Для даної системи другий закон Ньютона:

mx == kx ,

(3)

x = d 22x . dt

Якщо розділити рівняння (6.1.3) на m, отримаємо:

x =	− k	x ;		k	= ω 2	;
	m			m	0
x +ω0 x = 0 .			(4)

Це рівняння руху кульки під дією сили пружності.

Будь-яке тіло, що здійснює коливання згідно рівняння (4), називається лінійним гармонічним осцилятором.

Рішенням рівняння (4) є рівняння вигляду: x = Acos( ω0t +α) . (5)

Дане рівняння описує вільні незатухаючі гармонічні коливання. У рівнянні x – зміщення системи

від положення рівноваги в момент часу t; А– амплітуда коливань;	ωt	- кутова(циклічна) частота
	0

коливань; ω0t +α - фаза коливань; α - початкова фаза коливань.

Час T, протягом якого система здійснює одне повне коливання, називається періодом коливань. Число коливань за одиницю часу – частота ν = T1 .

Кутова частота ω пов’язана з періодом і частотою:

0

ω0 = 2Tπ = 2πν ,

1Гц – частота коливання, період якого дорівнює 1 сек.

Якщо рівняння (5) продиференціювати по часу, знайдемо швидкість і прискорення процесу:

v = x = dx = −Aω sin(ω t +α) ,			(7)
dt	0	0

a =

x =

d

2 x

= −Aω0

2

cos(ω0t +α) . (8)

dt 2

Позначимо

− Aω0

= v0

, тоді:

− Aω2

= a

0

0

ì x = Ac o sω(0t + α )

ï

π

ï

v0 c o sω(0t + α +

) .

ív =

2

(9)

ï

a

c o sω(

ïa =

0

0

t + α + π )

î

Тобто швидкість та прискорення теж змінюються за гармонічним законом, причому швидкість

π

випереджає переміщення по фазі на 2 , а прискорення і переміщення знаходяться в протифазі.

51

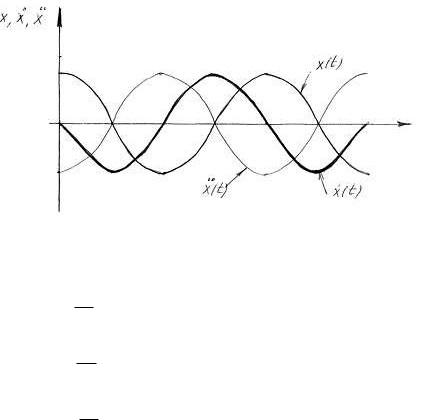
Рис. 3 Враховуючи співвідношення між частотами (6), систему (9) можемо записати:

ì			2π
ï x =	Aco s		(			t + α ) = Aco s2(π νt + α )
ï				T
				2π			π
ï
ív =	v0	co s		(		t + α +	2	)	.	(10)
ï					T
ï					2π
ïa =	a0	co s			(	t + α + π )
î					T

52

6.1.3. Енергія коливального руху На прикладі пружинного маятника можна показати, що робота пружної та квазіпружної сили за

повний цикл гармонічного коливання дорівнює нулю. Тоді ці сили є консервативними, а поля цих сил – потенціальні. Це означає, що для коливальної системи виконується закон збереження енергії.

W =Wп +Wк = const .

(11)

Виразимо значення енергії коливальної системи через її параметри. Для того, щоб надати зміщення x системі від початкового положення рівноваги необхідно виконати роботу проти сил поля:

x	x		2
A = òδA = −òFdx = +ò(−kx)dx = kx			.
0	0	2

Дана робота іде на надання даній системі запасу потенціальної енергії, тобто потенціальна енергія:

Wп =	kx	2	.	(12)
	2

Враховуючи рівняння (5) і те, що mω02 = k , можна записати:

Wп	=	ma2ω			2
		2		0	cos2 (ωt + α ) . (13)
		Кінетична енергія – енергія руху. Враховуючи вираз для швидкості з рівняння (7), знаходимо:
Wk	=	mv2	=		ma2ω 2	sin(ωt + α)
		2			0		.	(14)
					2
		На основі рівнянь (11), (13), (14), знаходимо, що повна енергія системи в будь-який момент часу:
W = 1 ma			2ω2 .			(15)
		2			0

З рівняння (15) видно, що повна енергія не залежить від часу, що відповідає закону збереження енергії замкненої системи.

Для коливальної системи потенціальну і кінетичну енергію можна виразити через повну енергію:

W	п	=W cos 2 (ω t +α) ,	(16)
		0
W	к	= W sin 2 (ω t +α) .	(17)
		0

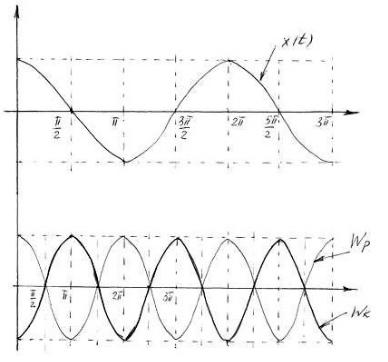
З даних формул витікає, що потенціальна і кінетична енергія змінюються у протифазі, а частота їх зміни в 2рази перевищує частоту гармонічних коливань.

Рис. 4

Середнє значення sin 2 + cos 2 дорівнює половині, і тоді середнє значення потенціальної енергії

дорівнює середньому значенню кінетичної енергії і дорівнює половині повної енергії.

Приведена довжина фізичного маятника – така довжина, при якій період коливань фізичного маятника дорівнює періоду коливань математичного маятника:

I

lпр = I 0 + l .

m

Лекція 10

6.2.Складання коливань

6.2.1.Векторна діаграма. Складання коливань одного напрямку

Будь-яке гармонічне коливання може бути представлене за допомогою вектора A , довжина якого дорівнює амплітуді. Напрям вектора утворює з віссю x кут, що дорівнює початковій фазі коливань:

x = Acos( ω0t +α) .

Якщо привести вектор A в коливальний рух з деякою швидкістю ω0 , то	проекція вектора на вісь x
буде змінюватись в межах від A до – A . Проекція кінця вектора A на	вісь x буде здійснювати
гармонічні коливання з амплітудою, яка дорівнює довжині A , циклічною частотою		ω
		0 , і фазою α .

Рис. 1

Такі векторні діаграми відображають собою уявлення коливань і операцій над ними у вигляді векторів і називаються векторними діаграмами.

Нехай матеріальна точка приймає участь у двох гармонічних коливаннях: x1 = A1 cos( ω0t +α1 )

x2 = A2 cos( ω0t +α2 )

з однаковою частотою і вздовж одного напряму.

Математична точка буде здійснювати результуюче коливання, яке можна записати: x = Acos( ω0t +α) .

Знайдемо вираз для амплітуди і початкової фази, скориставшись векторною діаграмою

Рис. 2

Результуючий вектор A дорівнює векторній сумі:

A = A1 + A2 ,

а амплітуда і початкову фазу α знаходимо на основі прямокутного трикутника OBC:

A2 = x2 + y2 = (x + x						2	)2		+ (y + y				2	)2	= (A cosα	1	+ A cosα		2	)2 + (A sinα		1	+ A sinα		2	)2 =
			1							1					1		2			1			2
= A2	+ A2	+ 2A A cos(α						1	+ α	2	).
1	2	1	2
	Рівняння для визначення початкової фази коливань (α2																	− α1 ):
α = arctg		A1 sinα1 + A2 sinα2										.
		A cosα		1	+ A cosα						2
		1					2
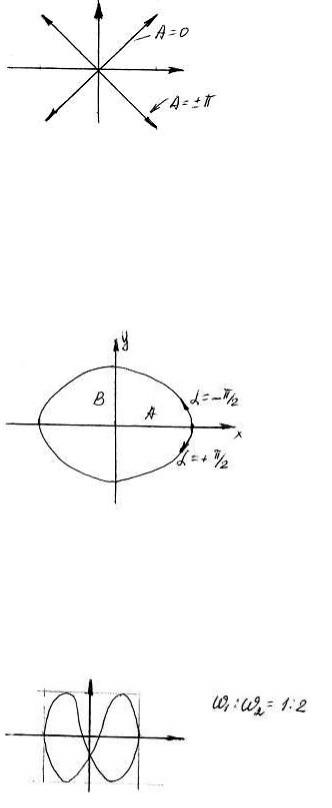
	Якщо проаналізувати цей вираз, то можемо																побачити,			що при	α2 -α1 = 0			коливання будуть
здійснюватись в одній і тій самій фазі. Амплітуда буде сумуватися: A = A1 + A2 . Якщо α2																										-α1 = ±π , то

коливання будуть знаходитись в протифазі, амплітуда буде: A = A1 − A2 . Якщо частоти коливань –

неоднакові ω1 ¹ ω2 , то вектори			A1	і A2	будуть обертатися з різною	швидкістю, тоді результуючий
вектор A буде		пульсувати по	своїй	величині і рухатись з несталою		швидкістю,	тоді результуюче
коливання –	не	гармонічне. Якщо частоти однакового напрямку, відрізняються не					досить помітно (
ω << ω ),	то	результат коливання		можна	розглядати як гармонічний з пульсуючою амплітудою,

коливання такого вигляду називають биттям.

6.2.2. Складання взаємно-перпендикулярних коливань Нехай матеріальна точка приймає участь в двох взаємо перпендикулярних коливаннях:

x = Acos ωt - перше коливання ,	(1)
y = B cos( ωt +α) - друге коливання	(2)
з однаковою частотою ω і різницею фаз	α (наприклад, коливання матеріальної точки відносно

положення рівноваги в одному напрямі і коливання в напрямі, що перпендикулярний до першого). В даному випадку матеріальна точку буде рухатись по деякій криволінійній траєкторії, рівняння якої в параметричній формі виражається рівняннями (1) і (2). Якщо видалити з них час t, то отримаємо рівняння траєкторії, що

виражається через різницю фаз α . На основі рівняння (2) знаходимо:

y	= cos(ωt + α) = cosωt cosα − sinωt sinα =	x			x2
			cosα − sinα	1−		.
B		A			A2

Перенесемо перший доданок у ліву частину рівняння і піднесемо до квадрату ліву і праву частини, і отримаємо рівняння результуючого коливання:

x2		y2		2xy	2
	+		−	AB cosα = sin		α
A2		B2
						.	(3)

Рівняння (3) – рівняння еліпса, півосі А і В якого не співпадають з координатними осями x і y. 1. α = 0

æ x

y

ö

2

ç

-

÷

= 0 .

B

è A

ø

Звідси маємо рівняння прямої:

y =

B

x .

(4)

A

Тобто

матеріальна

точка рухається вздовж

прямої,

відстань її

від початку координат

r =

cos ωt . Тобто результуючий рух є

гармонійним

коливанням вздовж прямої

x 2

+ y 2

= A2 + B 2

рівняння (3) з деякою частотою ω і амплітудою A =

.

A2 + B2

Рис. 3

2. α = ±π

рівняння (3) прийме вигляд:

æ x			y ö		2
ç		+		÷	= 0 .
	A
è			B ø

Результуючий рух буде представляти собою гармонічний рух вздовж прямої

y = -	B	x	(5)
	A

Рис. 4 3. α = ± π2

рівняння (3) прийме вигляд:

x2	+	y2	= 1	. (6)
A2		B2

Рівняння еліпса, що приведене до координатних осей x і y. Напівосі еліпса А і В відповідно дорівнюють амплітудам коливань, якщо амплітуди коливань однакові – еліпс перейде у коло.

Випадки α = ±	π	відрізняються лише напрямком руху по еліпсу, що витікає з рівнянь (1) і (2):
	2

Рис. 5	ω, то їх можна розглянути як
Якщо частоти коливань відрізняються на досить малу частоту
коливання з однією частотою, але з повільно змінюючоюся різницею фаз	ωt +α . Тоді рівняння (6.2.1) і
(6.2.2):
x = Acos ωt
y = B cos( ωt +( ωt +α)).

Результуючий рух в даному випадку буде відбуватися по змінній кривій, форма якої залежить лише від різниці фаз, що змінюються в межах (−π;π) . Якщо частоти відрізняються незначно, то траєкторія

приймає вигляд фігур Лісажу. При відношенні частот ω1 : ω2 = 1: 2

Рис. 6

Лекція 11 6.3. Згасаючі та вимушені коливання

6.3.1.Згасаючі коливання. Добротність

Убудь-якої коливальної системи є сили, які перешкоджають коливальному руху, наприклад, сили тертя в точці підвісу маятника, сили опору навколишнього середовища, тощо. Результуючою всіх цих систем називається затримуючою силою. Дія цієї сили викликає постійне затухання коливань. При малих швидкостях руху тіла, що знаходиться в коливальному русі затримуюча сила пропорційна швидкості руху:

Fзатр	=−rv =−r x

r- постійна величина для системи – коефіцієнт опору.

На систему діє квазіпружна та затримуюча сила, тоді другий закон Ньютона має вигляд:

mx = -kx - rx

. (1)

Поділимо на масу і отримаємо:

x = - mk x - mr x ,

+	k	= ω2	;	r	= 2β ,
	m	0		m

β - коефіцієнт затухання.

Маємо рівняння затухаючих коливань:

x = 2βx		+ω2 x = 0 , (2)
		0
ω	- величина власної частоти осцилятора.
0
	Так	як затримуюча сила викликає постійне зменшення амплітуди коливань ( A = A(t) ), тоді

розв’язок рівняння (2) будемо шукати:

x = A(t) cos( ωt +α) ,

(3)

ω - частота затухаючих коливань, ω ¹ ω0 .

Продиференціюємо рівняння (3) і підставивши значення x, x, x у рівняння (2), отримаємо:

[A + 2βA + A(ω02 − ω 2 )]cos(ωt + α) = 2ω(A + βA)sin(ωt + α ) = 0 .

Дане рівняння виходить при будь-яких значеннях t, якщо один з коефіцієнтів при тригонометричних функціях дорівнює нулю, тобто:

		(4)
A +βA =0 ,
так як 2ω ¹ 0 , то можна скоротити, тоді:
		2	2	) = 0 . (5)
A + 2βA + A(ω0 −ω
З рівняння (4)		знаходимо інші величини якщо			dA	= −βA , то	dA	= −βdt ,
					dt		A

A	dA	t	A		A		−βt
ò	A	= -β òdt Þ ln		= -βt Þ		= e		.	(6)
			A		A
A		0	0		0
0

Із рівняння (6) знайдемо залежність амплітуди від часу:

A(t) = A0 e−βt .

Знайдемо вираз для частоти ω : з рівняння (4) знаходимо:

A =−βA ;

			2	A .
A	= −βA = −β(−βA) = β
	Підставляємо в рівняння (6.3.5) і отримаємо:
β 2 A − 2β 2 A = −A(ω02 −ω2 ) .
	Звідси, скоротивши на А, маємо:
β 2	= ω02 -ω2 Þ ω =	ω02 - β 2		.		(7)

Дане рівняння використовують для реальної системи при умові, що відношення

β <ω0 .

r < k , тобто

2m m

При цих умовах, тобто при невеликому затуханні вільні затухаючі коливання описуються рівнянням:

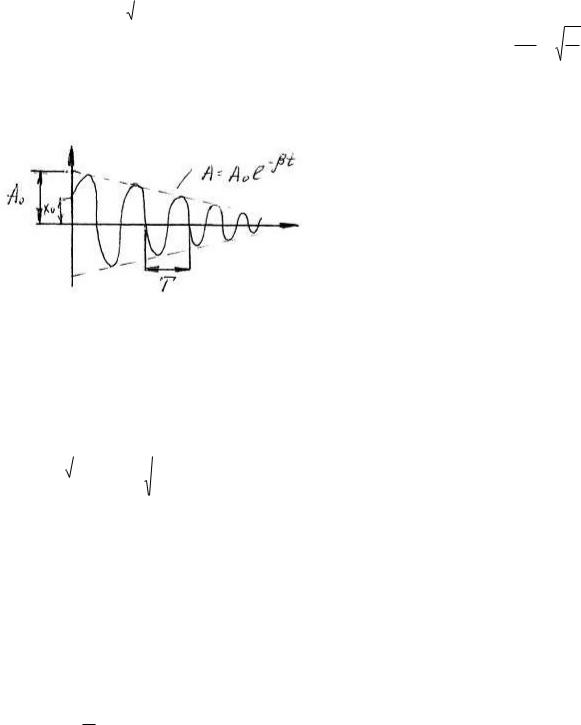
x = A e−βt cos( ωt +α) .	(8)
0

Графік даної функції має вигляд:

Рис. 1

При значенні t=0 початкове зміщення x0 : x0 = A0 cos α ,

A0 і початкова фаза α задаються початковими умовами: x(0) = x0 .

x(0) = x0

Період затухаючих коливань:

T =

2π

=

2π

=

2π

ω

ω02 - β 2

k

-

r 2 .

(9)

m

4m2

Відношення значень амплітуд відповідає моментам часу, що відрізняються на величину періоду:

	A(t)	= eβT .
	A(t +T )

Це відношення – дикримент затухання, а логарифм даного відношення:

	λ = ln	A(t)	= βT .
		A(t +T )

Це відношення – логарифмічний дикримент затухання.

Знайдемо деякий час τ , по закінченні якого амплітуда коливань зменшується в e=2,72 раз. Скористаємось формулою (6):

A e−βt	= eβτ = e ,
0
A e−β (t+τ )
0

тому, що τ = β1 , τ - час релаксації.

З урахуванням рівняння (10) знаходимо, що:

τ = Tλ .

Число коливань ( N e ) по закінченню яких амплітуда зменшується в e раз:

Ne = Tτ = λ1 . Величина

	Q =	π	=	π	= Neπ	(11)
		λ		βT

називають добротністю коливальної системи. Добротність пропорційна числу коливань, яке здійснює система за той час, по закінченню якого амплітуда зменшується в е раз.

6.3.2. Вимушені коливання Вимушеними називають коливання, які здійснюються під дією якоїсь зовнішньої сили, яка змінюється

в простому випадку по гармонійному закону:

Fx = Fm cos ωt .

Виникаючі при цьому коливання називають вимушеними. На дану частину тіла будуть діяти три сили: квазіпружна –kx, опору −rx , зовнішня вимушена сила Fx . З основного рівняння динаміки – другого

закону Ньютона:

mx = −kx −rx + Fm cos ωt . (12)

Або розділивши на масу Fmm = fm :

x + 2βx +ω02 x = fm cos ωt . (13)

Дослід показує, що по закінченню деякого часу, з початку дії вимушеної сили в системі встановлюється гармонічне коливання з частотою вимушеної сили, але які відстають по фазі від останнього

на величинуϕ . Таким чином:

x = Acos( ωt −ϕ)	(14)
Продиференціюємо рівняння (14) по часу і знайдемо швидкість і прискорення:
x = −Aωsin(ωt −ϕ) = Aωsin(ωt −ϕ +		π )	.	(15)
		2

x = −Aω2 cos(ωt −ϕ) = Aω2 cos(ωt −ϕ +π)

Підставимо вирази для початкового переміщення, швидкості і прискорення у рівняння (13). Сума трьох гармонічних функцій в лівій частині повинна дорівнювати силі f m cos ωt . Враховуючи фазові зміщення між початковим відхиленням, швидкістю і прискоренням, дане рівняння за допомогою векторної діаграми за умови, що ω <ω0 .

Рис. 2

Швидкість випереджає зміщення на величину π . Прискорення випереджає переміщення на величину π .

З даної діаграми за теоремою Піфагора слідує:

A2 (ω02 - ω 2 )2 + 4β 2 A2ω 2 = fm2 Þ
A =		fm			(16)
				.
		(ω02 - ω 2 )2 + 4β 2ω 2

З даної діаграми також видно, що відставання переміщення по фазі від вимушеної сили:

tgϕ =	2βω
		.	(17)
	(ω02 − ω2 )
Рівняння (16) і (17) показують, що амплітуда коливань і відставання зміщення по фазі на π
визначається властивостями			самого осцилятора, тобто ω0 , β, f m ,ω але ніякими не початковими

умовами. 6.3.3. Резонанс

Резонанс грає важливу роль в техніці.

Рис. 3

У даному випадку коефіцієнт затухання β1 < β2 < β3 . За даним графіком видно, що залежність амплітуди від частоти має максимум при частоті, яку можна знайти з умови ddAω = 0 . Дану частоту

називають резонансною частотою:

ωрез = ω02 − 2β 2 . (18)

Існуючий максимум амплітуди, який при цьому виникає, називається явищем резонансу – різке збільшення амплітуди під дією вимушеної сили, а графіки називаються резонансними кривими. Вираз для амплітуди при резонансі знайдемо підставивши рівняння (18) у (16):

	Amax =		fm			. (19)
		2β	ω02	− β 2

Чим менше затухання системи, тим більше виражений резонанс. Явище резонансу використовується в техніці коли потрібно збільшити коливання, або коли роблять так, щоб їх взагалі не було.

Залежність базового зсуву ϕ від частоти ω може бути показана кривими:

Рис. 4

При слабкому затуханні ωрез ≈ω0 і значення фазового зсуву ϕ при резонансі практично дорівнює

π2 .

Намалюємо графік залежності середньої потужності вимушеної сили від частоти: