50

Институт электронной техники

Кафедра ИПОВС

Лабораторная работа 3

«Моделирование поверхности 3D-объекта. Сплайновые кривые и сплайновые поверхности»

Содержание

11. Регулярная поверхность в параметрическом виде __________________ стр. 32

12.Сплайновые поверхности _______________ _______________ стр. 34

13. Бикубическая поверхность Безье__________________ стр. 35

14.Бикубическая B-сплайновая поверхность____________________ стр. 43

15. __________________________________ стр. 27

16. _________________ стр. 29

17. ______________________ стр.34

Регулярная поверхность в параметрическом виде.

Регулярной поверхностью называется множество точек M(x,y,z) 3-х мерного пространства, координатыx,y,zкоторых определяются из следующих соотношений:

(61)

Здесь x(u,v),y(u,v),z(u,v), – гладкие функции своих аргументов, причем выполняется соотношение:

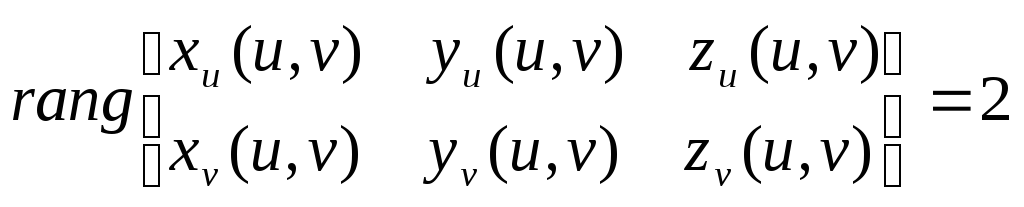(62)

Область D– это некоторая область на плоскости параметровu,v.

Уравнения (61) называются параметрическими уравнениями поверхности. Их часто записывают в векторной форме:

(63)

В этом случае точка Mна поверхности будет определяться двумя параметрамиM(u,v).

Для примера рассмотрим поверхность сферы с радиусом R. Уравнение сферы имеет вид:

(63)

В качестве параметров удобно выбрать сферические координаты u=,v=. Тогда параметрические уравнения (61) примут следующий вид:

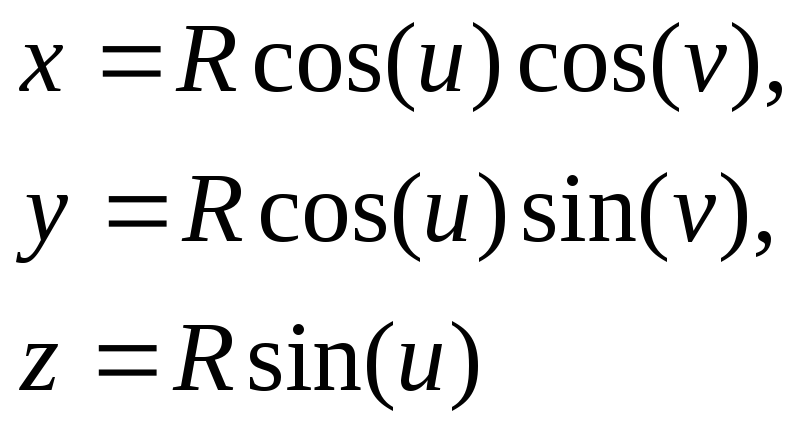(64)

Пусть областью изменения параметров u,vбудет следующая областьD:

(65)

На Рис.33 изображена эта область Dна плоскости параметровu,v.

На Рис.34 изображена часть сферической поверхности, на которую параметрические уравнения (64) отображают точки области D.

В области Dизображены также две линииu=constиv=const. При помощи этих линий можно построить координатную сетку в областиD. Затем эту сетку можно отобразить на элементе сферической поверхности с помощью уравнений (64).

На Рис.34 показана такая координатная сетка, нарисованная желтыми линиями. Благодаря этой координатной сетке, элемент сферической поверхности выглядит как 3-х мерный объект.

Если вычислить частные производные по параметрам (u,v) от радиуса-вектораr(u,v) (63), то можно найти касательные векторы к рассматриваемой поверхности.

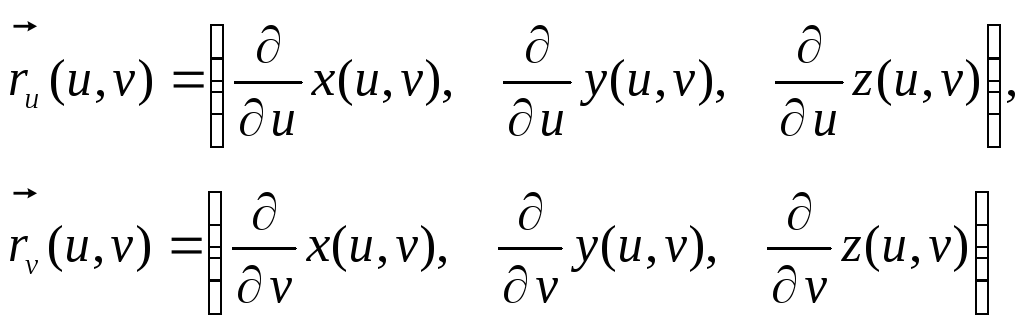(66)

На Рис.34 изображены два касательных вектора, построенных с помощью формул (66). Причем вектор ruявляется касательным вектором к координатной линииv=const, а векторrvявляется касательным вектором к координатной линииu=const.

Рис.33 Область Dизменения параметров (u,v).

Рис.34 Элемент сферической поверхности. Касательная плоскость. Касательные векторы ru,rvи нормальный векторN.

(Изображение на Рис. 34 создано программой gr3D01.cpp.)

На Рис.34 показан также вектор нормалиNк рассматриваемой поверхности. Вектор нормали можно найти как векторное произведение касательных векторов:

(67)

Для нахождения проекций вектора нормали удобно записать векторное произведение (67) в форме определителя:

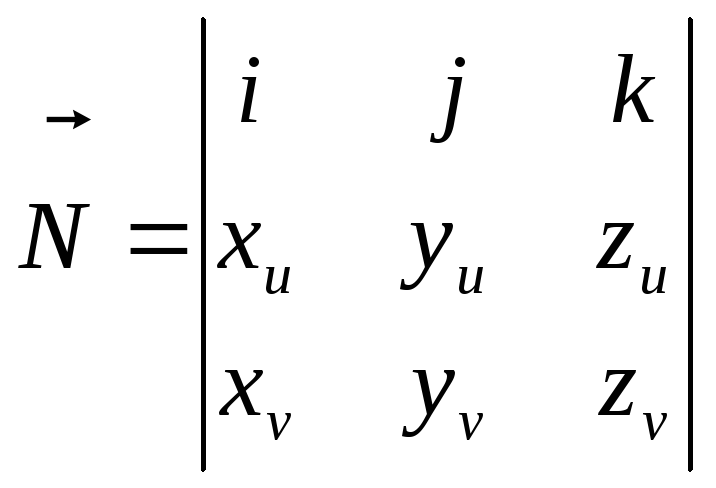(68)

Изображенный на Рис.34 вектор нормали построен с помощью формул (68).

Условие (62) в определении регулярной поверхности, означает, что в каждой точке Mрегулярной поверхности существует касательная плоскость, и эта плоскость при непрерывном перемещении по поверхности текущей точкиMизменяется непрерывно. Непрерывно при этом изменяются касательные векторы и вектор нормали.

Покажем, как можно найти уравнение касательной плоскости, проходящей через точку M, принадлежащую этой поверхности. Пусть координаты это точки равныM(x₀,y₀,z₀). Пусть также известен вектор нормалиNк поверхности в этой точке. Тогда уравнение касательной плоскости будет иметь следующий вид:

(69)

Плоскость является 2-х мерным объектом, поэтому ее можно, как и любую поверхность, описать двумя параметрами с помощью параметрических уравнений. Пусть этими параметрами будут параметры pиq. Тогда используя касательные векторыив точке M(x₀,y₀,z₀), параметрические уравнения касательной плоскости (69) можно записать в следующем виде:

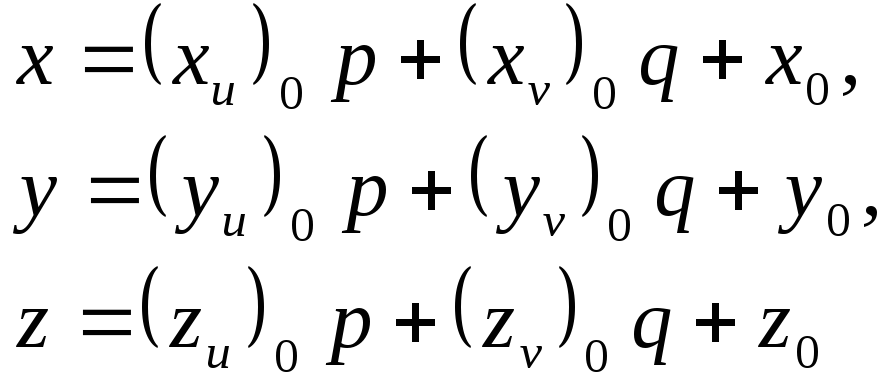(70)

Изображенная на Рис.34 касательная плоскость построена с помощью формул (70).