35

Московский институт электронной техники

Кафедра ИПОВС

Лабораторная работа 2

«Композиция двухмерных аффинных преобразований. Моделирование движения объектов в плоскости».

Содержание

1. Аффинные преобразования на плоскости ………………………………….. стр. 2.

2. Два взгляда на аффинные преобразования ………………………………….. стр. 3.

3. Элементарные аффинные преобразования …………………………………… стр. 5

4. Однородные координаты ……………………………………………………… стр. 8.

5. Композиция элементарных аффинных преобразований ……………………. стр. 10.

6. Класс Matrix2Dи аффинные преобразования в 2Dграфике ………………… стр.12.

7. Пример аффинных преобразований в 2D-графике …………………………. стр. 13.

8. Пример программы моделирования движения в Windows………………… стр. 17

11. Уничтожение следа за движущимся объектом повторным рисованием …. стр. 19

13. Использование режима XORдля моделирования движения ……………… стр. 21

15. Использование оперативной памяти для моделирования движения ……… стр. 23

16. Примеры анимации в Windowsпрограммах ………………………………… стр. 25

17. Задание к выполнению лабораторной работы ………………………………. стр.28

Аффинные преобразования на плоскости.

В компьютерной графике все, что связано с построением и обработкой изображений в плоскости принято называть 2D-графикой (2-Dimensional). В этой лабораторной работе мы будем рассматривать методы построения изображения движущихся объектов в 2D-графике. Допустим, что на плоскости введена прямолинейная система координат.

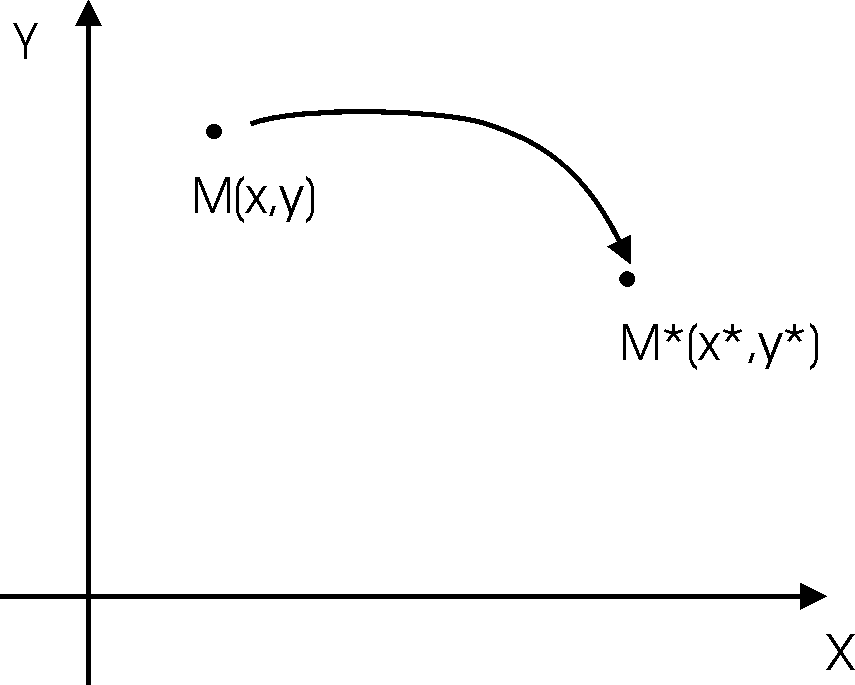
Рис. 1.

Движение точки M(x,y).

Тогда каждой точке Mставится в соответствие упорядоченная пара чисел (x,y) - ее координаты (Рис. 1). Совершим над координатами точкиMследующее линейное преобразование.

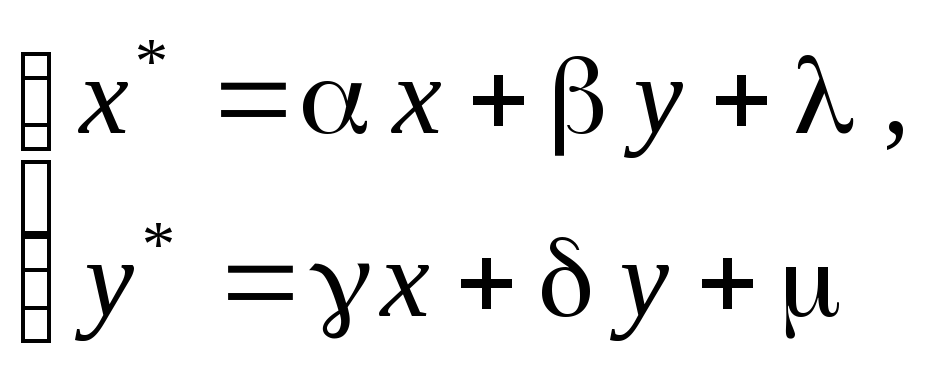(1)

В результате мы получим другую точку M^*с координатами (x^*,y^*). Преобразование (1) можно рассматривать как математическое описание движения точкиMиз одного места в другое.

Будем предполагать, что определитель, составленный из коэффициентов ,,,отличен от нуля.

(2)

Тогда условие (2) означает, что существует обратное преобразование.

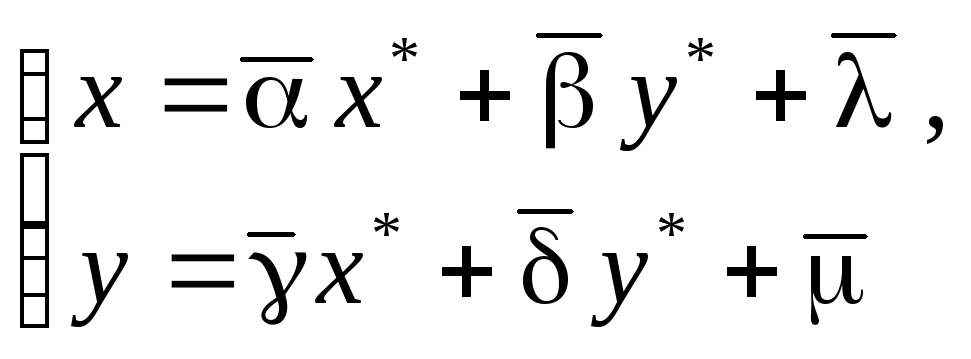(3)

Преобразование (3) можно рассматривать как математическое описание обратного движения точки M.

Линейное преобразование (1) вместе с условием (2) называется аффинным преобразованием. В математической литературе аффинным преобразованиемназывают взаимно однозначное отображение плоскости на себя, при котором трем точкам на одной прямой соответствуют три точки тоже лежащие на одной прямой (Рис. 2).

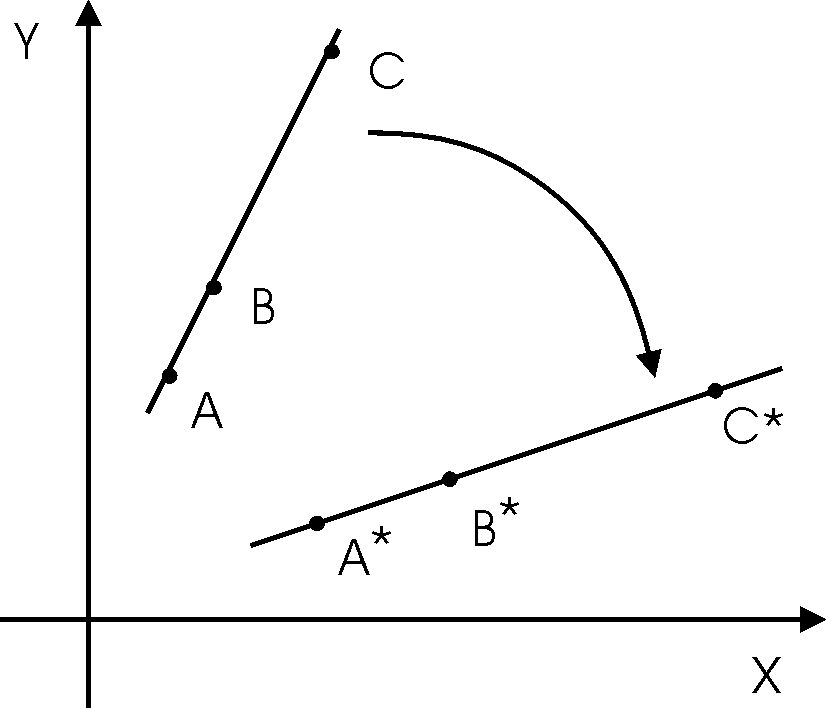
Рис. 2.

Аффинное преобразование. Трем точкам на одной прямой соответствуют три точки, лежащие на одной прямой.

Легко проверить, что линейное преобразование (1) отвечает указанному свойству аффинного преобразования. Укажем еще одно свойство аффинного преобразования. Аффинное преобразование переводит скрещивающиеся прямые в скрещивающиеся, а параллельные линии в параллельные линии (Рис. 3).

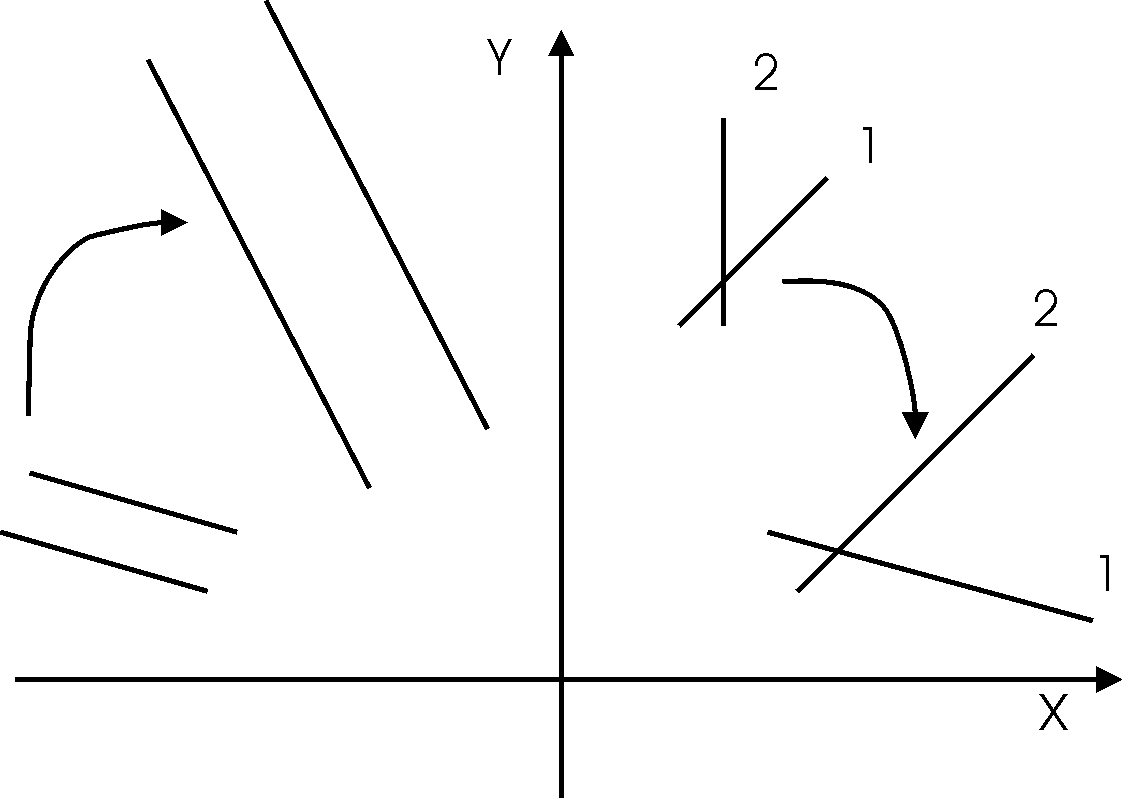
Рис. 3.

Аффинное преобразование. Параллельные линии переходят в параллельные, скрещивающиеся в скрещивающиеся.

Два взгляда на аффинные преобразования.

Формулы линейного преобразования (1) можно интерпретировать двумя способами. Во-первых, в неподвижной системе координат движутся точки по заданному закону движения. Во-вторых, точки объекта неподвижны, а поворачивается система координат в обратную сторону.

Рассмотрим первую интерпретацию аффинного преобразования – неподвижна система координат, а движутся точки объекта. На рисунках 1, 2, 3 изображена именно такая ситуация, движутся объекты – точки и линии. Для примера, изобразим простейший объект – треугольник ABC, который поворачивается на угол в 45по часовой стрелке вокруг начала координат и оказывается в положении треугольникаA^*B^*C^*(Рис. 4).

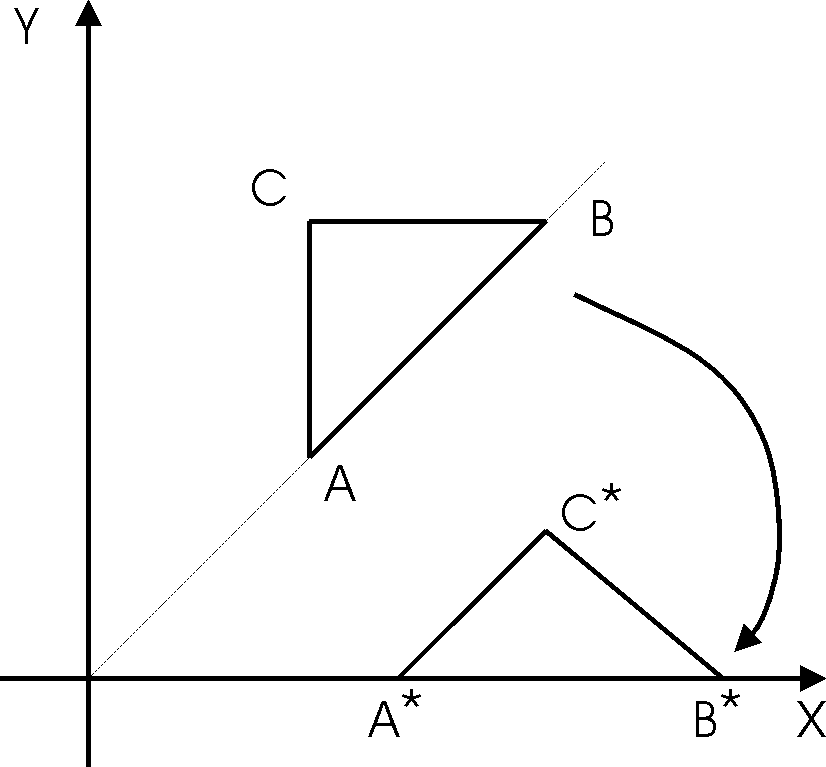
Рис. 4.

Движение треугольника в неподвижной системе координат.

Относительно неподвижной системы координат (x,y) после аффинного преобразования треугольник занимает новое положение, а именно лежит на осиx. Вершины треугольника теперь имеют новые координаты (x^*,y^*). Для каждой вершины мы получили преобразование координат

(4)

Теперь дадим другую интерпретацию аффинным преобразованиям (1). Будем считать треугольник ABCнеподвижным относительно системы координат (x,y), и введем новую систему координат (x^*,y^*). Эту систему координат получим из старой системы координат, повернув ее на угол в 45против часовой стрелки вокруг начала координат (Рис. 5).

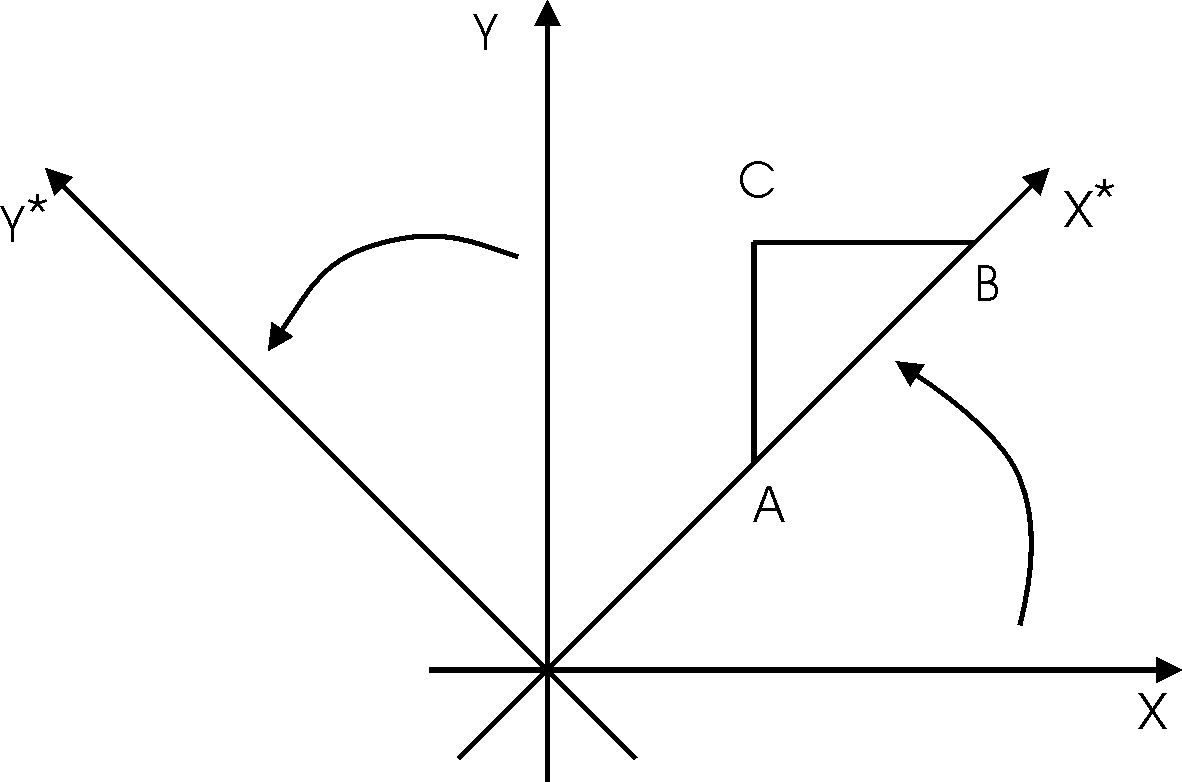
Рис. 5.

Неподвижный треугольник в разных системах координат.

В новой системе координат вершины треугольника ABCбудут иметь другие координаты. Легко видеть, что относительно новой системы координат (x^*,y^*) треугольникABCрасполагается точно так же, как треугольникаA^*B^*C^*(рис. 4) располагался относительно старой системы координат (x,y). Поэтому цепочка преобразований координат будет точно такой же, как и цепочка (4).

Подведем итог. Аффинное преобразование (1) можно рассматривать или как движение объекта в одном направлении (поворот на 45), или как преобразование системы координат в противоположном направлении (поворот на -45).

В 3D-графике первому случаю соответствует ситуация когда наблюдатель стоит на месте, связанный с неподвижной системой координат, а движутся объекты, например вращаются перед наблюдателем.

Второму случаю в 3D-графике соответствует ситуация когда неподвижны объекты, а наблюдатель вместе с подвижной системой координат движется вокруг объектов наблюдая их с разных сторон.

Наконец отметим, что при композиции аффинных преобразований, моделирующих сложное движение как в 2D- так и в 3D-графике необходимо использовать обе точки зрения на аффинное преобразование. Это мы покажем дальше.