Семестровая работа. Вариант №31221

Вариант №31221

Задание: Построить математическую модель нагрева теплотехнически толстого тела в форме пластины в условиях конвективного теплообмена и разработать алгоритм решения полученной системы дифференциальных уравнений методом конечных разностей с использованием явной разностной схемы.

Решение:

— Дифференциальное уравнение теплопроводности, используемое при моделировании процесса нагрева теплотехнически толстого тела:

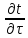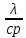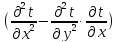= ∙ , (1)

где: t = t (x, y, z) – температура, ̊С;

τ – время нагрева, с;

x, y, z – координаты точки тела, м;

λ – теплопроводность металла, Вт/(м∙К);

с – теплоёмкость металла, Дж/(кг∙К);

p – плотность металла, кг/м³;

— Т.к. в практике термической обработки путём подбора значения толщины нагреваемого слоя S сводят рассмотрение нагрева садки печи к рассмотрению нагрева бесконечной плоской пластины, то этим решение трехмерной задачи сводится к решению одномерной и уравнение (1) принимает вид:

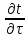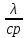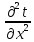= ∙ , (2)

где: t = t (x, τ) и 0 < x < S.

— Начальные условия охлаждения:

t(x, 0) = t₀. (3)

— Граничные условия охлаждения:

– λ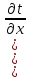 = q_пов, (4)

где q_пов – удельный тепловой поток, Вт/м²;

– λ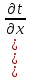 = 0. (5)

— Удельный тепловой поток в печи с постоянной температурой в условиях конвективного теплообмена:

q_пов = α_к [t_c – t(0,τ)], (6)

где α_к – коэффициент теплоотдачи конвекцией, Вт/(м²∙К);

t_c – температура среды, ̊С.

Система уравнений (2) – (6) представляет собой математическую модель процесса нагрева теплотехнически толстого тела в форме пластины в условиях конвективного теплообмена в печи с постоянной температурой.

Для решения этой системы наиболее подходящим является метод конечных разностей, в основе которого лежит конечно-разностная аппроксимация производных.

Для реализации данного метода необходимо разбить нагреваемое тело на слои толщиной h и построить в координатно-временном пространстве сетку с размерами ячейки h × k, где k – шаг численного интегрирования по времени.

Рисунок 1 – Вид конечно-разностной сетки

— Для узлов сетки, расположенных на оси x и соответствующих τ = 0, температура равна t₀.

— Для узлов сетки, соответствующих внутренним точкам нагреваемого тела:

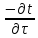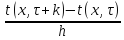= , (7)

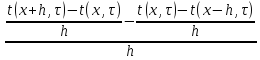= , (8)

Подставив (7), (8) в (2) и приняв шаг сетки по времени равным:

k = 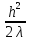∙cp, (9)

получим:

t(x, τ + k) = 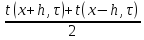. (10)

Выражение (10) позволяет для каждого момента времени рассчитать значение температуры в любом внутреннем узле сетки, если известно распределение температур для предыдущего момента времени.

— Значение температуры в узлах, соответствующих x = 0 и x = S, находятся из кривых условий (4), (5).

Поскольку в этом случае:

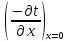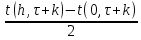= , (11)

= , (12)

то из (4) и (5) следует:

t(0, τ + k) = t(h, τ + k) + q_пов ∙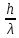, (13)

t(S, τ+k) = t(S–h, τ+k). (14)

Уравнение (13) после подстановки в него (6) принимает вид:

t(0, τ+k) = t(h, τ+k) +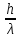 {α_к[t_c – t(0, τ+k)]} (15)

и становится нелинейным уравнением относительно t(0,τ + h). Для его решения могут быть использованы разные методы, наиболее простым из которых является метод итерации. Суть его состоит в том, что для каждого момента времени τ первоначально принимается

t(0, τ+k) = t(0, τ). (16)

Затем это значение подставляется в (15) и находится новое приближение для t = (0, τ+k), которое опять подставляется в ту же формулу. Подобная процедура повторяется несколько раз до получения значения t(0, τ+k) с заданной точностью.

Таким образом, рассчитывая поэтапно t(x,τ), начиная с τ=k, можно проследить изменение температуры тела по глубине и по времени в процессе нагрева. Точность расчётов увеличивается с уменьшением величины h и k, а выполнение условия (9) обеспечивает сходимость численного решения рассматриваемой системы дифференциальных уравнений.

7