
отчёт_lab1
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра высшей математики №2
отчет
по лабораторной работе №1
по дисциплине «Статистика случайных процессов»
Тема: Исследование характеристик случайных процессов
|
Студент гр. 3381 |
|
Сучков А.И. |
|
Преподаватель |
|
Егоров В.А. |
Санкт-Петербург
2018
Цель работы.
Научится находить различные характеристики случайных процессов, такие как математическое ожидание, дисперсия, корреляционная функция (в том числе и нормированная), спектральная плотность.
Основные теоретические положения.
Функция
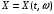 ,
где
,
где
 ,
,
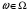 (t
– время,
(t
– время,
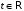 или
или
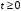 ,
Ω – пространство
элементарных событий) называется
случайным процессом (с.п.). В дальнейшем
с.п.
,
Ω – пространство
элементарных событий) называется
случайным процессом (с.п.). В дальнейшем
с.п.
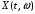 будем обозначать сокращенно
будем обозначать сокращенно
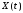 или X.
или X.
Рассматриваются
случайные процессы с действительными
значениями. При фиксированном значении
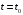
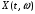 является случайной величиной, которая
называется сечением случайного процесса
в момент времени t0.
При фиксированном значении
является случайной величиной, которая
называется сечением случайного процесса
в момент времени t0.
При фиксированном значении

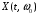 является неслучайной (обычной) функцией
от времени t,
которая называется реализацией случайного
процесса.
является неслучайной (обычной) функцией
от времени t,
которая называется реализацией случайного
процесса.
При
фиксированном значении t
сечение
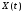 является случайной величиной. Пусть
для любого
является случайной величиной. Пусть
для любого
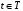 существует математическое ожидание
существует математическое ожидание
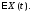 Математическим ожиданием с.п.
Математическим ожиданием с.п.
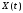 называется неслучайная функция от
времени t:
называется неслучайная функция от
времени t:
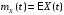 .
.
Свойства
математического ожидания (м.о.) с.п. Пусть
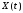 ,
,
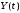 – случайные
процессы,
– случайные
процессы,
 – неслучайная функция,
– неслучайная функция,
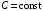 :
:
-
 ;
; -
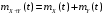 ;
; -
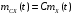 ;
; -
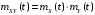 ,
если сечения
,
если сечения
 ,
,
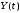 некоррелированы при каждом
некоррелированы при каждом
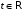 ;
; -
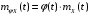 .
.
Пусть
при каждом фиксированном t
для сечения
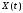 определена дисперсия
определена дисперсия
 .
Дисперсией с.п.
.
Дисперсией с.п.
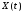 называется неслучайная функция от
времени t:
называется неслучайная функция от
времени t:
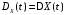 .
.
Среднеквадратическим
отклонением с.п.
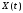 называется величина:
называется величина:
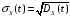 .
.
Свойства
дисперсии с.п. Пусть
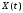 ,
,
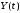 – случайные
процессы,
– случайные
процессы,
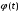 – неслучайная
функция,
– неслучайная
функция,
 :
:
-
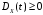 ;
; -
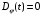 ;
; -
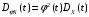 ;
; -
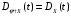 ;
; -
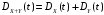 ,
если сечения
,
если сечения
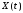 ,
,
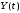 некоррелированы при каждом
некоррелированы при каждом
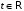 .
.
Пусть
 – центрированный с.п. Корреляционной
функцией с.п.
– центрированный с.п. Корреляционной
функцией с.п.
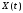 называется неслучайная функция от двух
аргументов t1,
t2:
называется неслучайная функция от двух
аргументов t1,
t2:
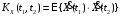 .
.
Нормированной
корреляционной функцией с.п.
 называется неслучайная функция:
называется неслучайная функция:
 .
.
Свойства
корреляционной функции с.п. Пусть
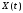 – случайный процесс, U
– случайная величина,
– случайный процесс, U
– случайная величина,
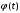 – неслучайная функция:
– неслучайная функция:
-
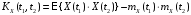 ;
; -
 ;
; -
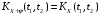 ;
; -
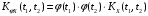 ;
; -
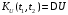 ;
; -
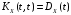 ;
; -
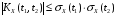 ;
; -
 .
.
Пусть
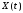 ,
,
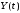 – случайные процессы. Взаимной
корреляционной функцией с. п.
– случайные процессы. Взаимной
корреляционной функцией с. п.
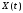 ,
,
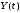 называется неслучайная функция от двух
аргументов t1,
t2:
называется неслучайная функция от двух
аргументов t1,
t2:
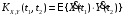 .
.
Два
с.п.
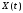 ,
,
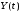 называются некоррелированными, если
называются некоррелированными, если
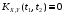 .
Нормированной взаимной корреляционной
функцией с.п.
.
Нормированной взаимной корреляционной
функцией с.п.
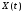 ,
,
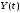 называется неслучайная функция:
называется неслучайная функция:
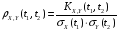 .
.
Свойства
взаимной корреляционной функции. Пусть
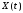 ,
,
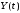 – случайные процессы,
– случайные процессы,
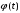 ,
,
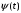 – неслучайные функции:
– неслучайные функции:
-
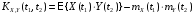
-
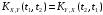 ;
; -
 ;
; -
 ;
; -
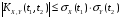 ;
; -
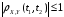 .
.
Пусть
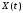 – случайный процесс,
– случайный процесс,
 – его производная. Тогда верны следующие
свойства:
– его производная. Тогда верны следующие
свойства:
-
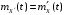 ;
; -
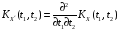 ;
; -
 .
.
Пусть
 – случайный процесс,
– случайный процесс,
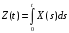 .
Тогда выполняются следующие свойства:
.
Тогда выполняются следующие свойства:
-
 ;
; -
 ;
; -
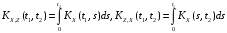 .
.
Постановка задачи.
Задание
№1: Найти
математическое ожидание
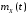 ,
корреляционную функцию
,
корреляционную функцию
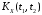 ,
дисперсию
,
дисперсию
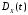 случайного процесса
случайного процесса
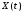 ,
где U, V – некоррелированные
случайные величины.
,
где U, V – некоррелированные
случайные величины.
Задание
№2: Найти
корреляционную функцию
 и дисперсию
и дисперсию
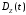 ,
если
,
если
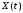 и
и
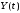 – некоррелированные случайные процессы
и даны корреляционные функции
– некоррелированные случайные процессы
и даны корреляционные функции
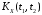 и
и
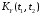 .
.
Задание
№3:
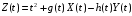 ,
где g(t),
h(t)
– неслучайные функции; X(t),
Y(t)
– центрированные случайные процессы
с корреляционными функциями
,
где g(t),
h(t)
– неслучайные функции; X(t),
Y(t)
– центрированные случайные процессы
с корреляционными функциями
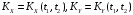 и взаимной корреляционной функцией
и взаимной корреляционной функцией
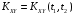 .
Найти математическое ожидание
.
Найти математическое ожидание
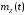 ,
корреляционную функцию
,
корреляционную функцию
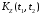 ,
дисперсию
,
дисперсию
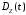 ,
нормированную корреляционную функцию
,
нормированную корреляционную функцию
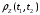 случайного процесса
случайного процесса
 .
.
Задание
№4: Найти
математическое ожидание
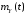 ,
корреляционную функцию
,
корреляционную функцию
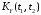 ,
дисперсию
,
дисперсию
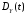 ,
нормированную корреляционную функцию
,
нормированную корреляционную функцию
 случайного процесса
случайного процесса
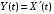 ,
не дифференцируя
,
не дифференцируя
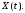 Найти взаимную корреляционную функцию
Найти взаимную корреляционную функцию
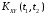 и нормированную взаимную корреляционную
функцию
и нормированную взаимную корреляционную
функцию
 .
U
– случайная величина.
.
U
– случайная величина.
Задание
№5:
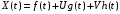 ,
где f(t),
g(t),
h(t)
– неслучайные функции; U,
V
– некоррелированные случайные величины
(см. табл. 1). Найти математическое
ожидание
,
где f(t),
g(t),
h(t)
– неслучайные функции; U,
V
– некоррелированные случайные величины
(см. табл. 1). Найти математическое
ожидание
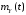 ,
корреляционную функцию
,
корреляционную функцию
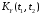 ,
дисперсию
,
дисперсию
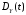 случайного процесса
случайного процесса
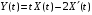 ,
не дифференцируя X(t).
,
не дифференцируя X(t).
Задание
№6:
 ,
где f(t)
– неслучайная функция; U
– случайная
величина,
,
где f(t)
– неслучайная функция; U
– случайная
величина,
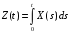 .
.
Найти
математическое ожидание
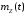 ,
корреляционную функцию
,
корреляционную функцию
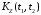 ,
дисперсию
,
дисперсию
 ,
взаимные корреляционные функции
,
взаимные корреляционные функции
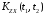 и
и
 не
интегрируя X(t).
не
интегрируя X(t).
Задание
№7:
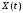 – случайная величина; U
– случайная
величина;
– случайная величина; U
– случайная
величина;
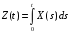 .
.
Найти
корреляционную функцию
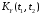 ,
дисперсию
,
дисперсию
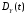 ,
нормированную корреляционную функцию
,
нормированную корреляционную функцию
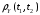 случайного процесса
случайного процесса
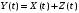 ,
не интегрируя X(t).
,
не интегрируя X(t).
Задание
№8: Доказать,
что случайный процесс
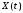 стационарен в широком смысле. Проверить
свойство эргодичности для математического
ожидания, корреляционной функции. Найти
дисперсию случайного процесса. U, V
– некоррелированные случайные величины.
стационарен в широком смысле. Проверить
свойство эргодичности для математического
ожидания, корреляционной функции. Найти
дисперсию случайного процесса. U, V
– некоррелированные случайные величины.
Задание
№9:
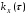 – корреляционная функция стационарного
случайного процесса
– корреляционная функция стационарного
случайного процесса
 .
Найти корреляционную функцию, дисперсию
производной
.
Найти корреляционную функцию, дисперсию
производной
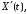 взаимную корреляционную функцию
взаимную корреляционную функцию
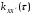 .
.
Задание
№10:
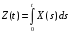 .
Найти корреляционную функцию, дисперсию
случайного процесса
.
Найти корреляционную функцию, дисперсию
случайного процесса
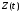 ,
взаимную корреляционную функцию
,
взаимную корреляционную функцию
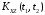 .
В задачах, в которых корреляционная
функция
.
В задачах, в которых корреляционная
функция
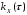 содержит
содержит
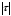 ,
рассмотреть только случай
,
рассмотреть только случай
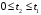 .
.
Задание
№11:
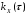 – корреляционная функция стационарного
случайного процесса
– корреляционная функция стационарного
случайного процесса
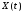 .
Найти его спектральную плотность.
.
Найти его спектральную плотность.
Выполнение работы.
Задание №1
Дано:
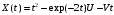 ;
;
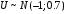 ;
;
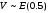
Решение:
Сначала
необходимо вычислить математические
ожидания и дисперсии случайных величин
U
и V:
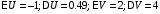 .
.
Математическое ожидание от суммы случайных процессов равно сумме математических ожиданий от слагаемых:
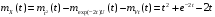 .
.
Теперь необходимо найти корреляционную функцию. Поскольку прибавление к случайному процессу неслучайной функции t2 не влияет на корреляционную функцию, получаем:
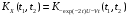 .
.
Так
как случайные процессы
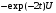 и
и
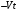 некоррелированы из-за некоррелированности
случайных величин U,
V,
получим:
некоррелированы из-за некоррелированности
случайных величин U,
V,
получим:
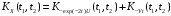 ,
,
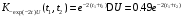 ;
;
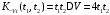 .
.
Таким образом,
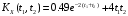 .
.
Поскольку,
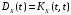 ,
получим:
,
получим:
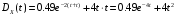
Задание №2
Дано:
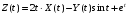 ;
;
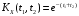 ;
;
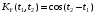
Решение:
Прибавление к случайному процессу
неслучайной функции et
не влияет на корреляционную функцию.
Далее, из-за некоррелированности
случайных процессов
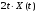 и
и
 имеем:
имеем:
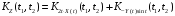 ;
;
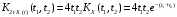 ,
,
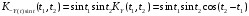 .
.
Таким образом,
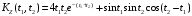 .
.
Поскольку,
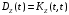 ,
получим:
,
получим:
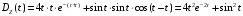 .
.
Задание №3
Дано:
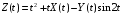 ;
;
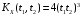 ;
;
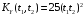 ;
;

Решение: Так как X(t), Y(t) – центрированные случайные процессы, то их математические ожидания равны нулю. Таким образом:
 .
.
Прибавление
неслучайной функции t2
к случайному процессу
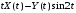 не меняет его корреляционной функции,
то получаем:
не меняет его корреляционной функции,
то получаем:
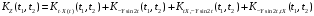 ;
;
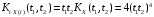 ;
;
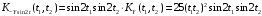 ;
;
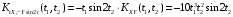 ;
;
 .
.
Таким образом,
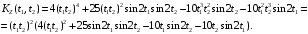
Поскольку,
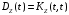 ,
получим:
,
получим:
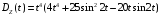 .
.
По определению нормированной корреляционной функции:
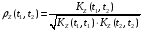 .
.
Таким образом,
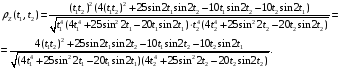
Задание №4
Дано:
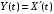 ;
;
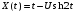 ;
;

Решение:
Сначала
необходимо вычислить математическое
ожидание и дисперсию случайной величины
U:
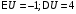 .
.
Математическое ожидание случайного процесса X(t):
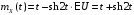 .
.
Корреляционная функция случайного процесса X(t):
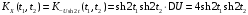 .
.
Дисперсия случайного процесса X(t) имеет вид:
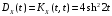 .
.
Поскольку,
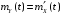 ,
получим:
,
получим:
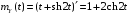 .
.
Поскольку,
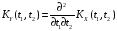 ,
получим:
,
получим:
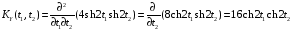 .
.
Дисперсия случайного процесса Y(t):
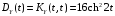 .
.
Нормированная корреляционная функция имеет вид:
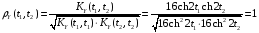 .
.
Взаимная корреляционная функция имеет вид:
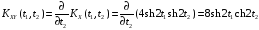 .
.
Нормированная взаимная корреляционная функция имеет вид:
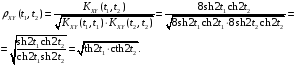
Задание №5
Дано:
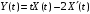 ;
;
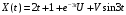 ;
;
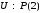 ;
;
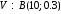
Решение:
Сначала
необходимо вычислить математические
ожидания и дисперсии случайных величин
U
и V:
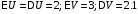 .
.
Математическое ожидание случайного процесса X(t) имеет вид:
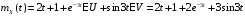 .
.
Корреляционная функция случайного процесса X(t) имеет вид:

Математическое ожидание производной случайного процесса X(t) имеет вид:
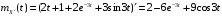 .
.
Корреляционная функция производной случайного процесса X(t) имеет вид:
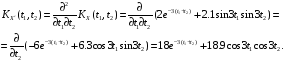
Взаимные корреляционные функции случайного процесса X(t) и его производной имеют вид:
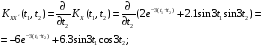
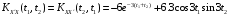 .
.
Математическое ожидание случайного процесса Y(t) имеет вид:
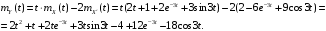
Корреляционная функция случайного процесса Y(t) имеет вид:
 ;
;
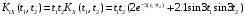 ;
;
 ;
;
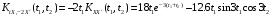 ;
;
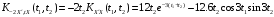 ;
;
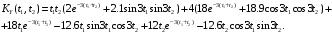
Дисперсия случайного процесса Y(t) имеет вид:
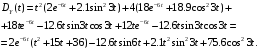
Задание №6
Дано:
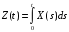 ;
;
 ;
;

Решение:
Сначала необходимо вычислить математическое
ожидание и дисперсию случайной величины
U:
 .
.
Математическое ожидание случайного процесса X(t) имеет вид:
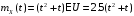 .
.
Корреляционная функция случайного процесса X(t) имеет вид:
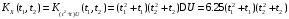 .
.
Математическое ожидание случайного процесса Z(t) имеет вид:
 .
.
Корреляционная функция случайного процесса Z(t) имеет вид:
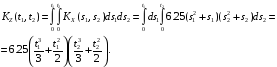
Дисперсия случайного процесса Z(t) имеет вид:
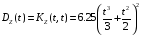 .
.
Взаимные корреляционные функции случайных процессов X(t) и Z(t) имеют вид:
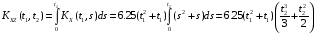 ;
;
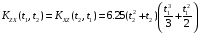 .
.
Задание №7
Дано:
 ;
;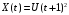 ;
;
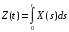 ;
;

Решение: Корреляционная функция случайного процесса X(t) имеет вид:
 .
.
Корреляционная функция случайного процесса Z(t) имеет вид:
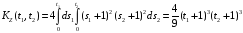 .
.
Взаимные корреляционные функции случайных процессов X(t) и Z(t) имеют вид:
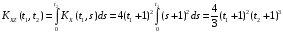 ;
;
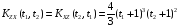 .
.
Корреляционная функция случайного процесса Y(t) имеет вид:
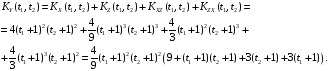
Дисперсия случайного процесса Y(t) имеет вид:
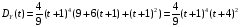 .
.
Нормированная взаимная корреляционная функция имеет вид:
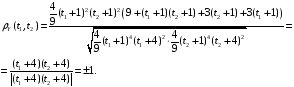
Задание №8
Дано:
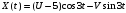 ;
;
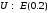 ;
;
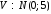
Доказательство:
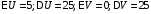 .
.
Математическое ожидание случайного процесса X(t) имеет вид:
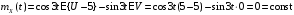 .
.
Корреляционная функция случайного процесса X(t) имеет вид:
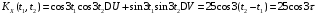 .
.
Таким
образом,
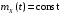 ,
а корреляционная функция зависит только
от (t2 – t1),
следовательно, случайный процесс X(t)
стационарен в широком смысле.
,
а корреляционная функция зависит только
от (t2 – t1),
следовательно, случайный процесс X(t)
стационарен в широком смысле.
Необходимо
проверить свойство эргодичности
относительно математического ожидания
mX.
Пусть
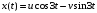 – реализация случайного процесса X(t).
Преобразование:
– реализация случайного процесса X(t).
Преобразование:
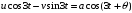 ,
,
где
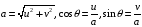 .
Стационарный случайный процесс X(t)
называется эргодическим относительно
математического ожидания mX,
если для любой его реализации x(t)
.
Стационарный случайный процесс X(t)
называется эргодическим относительно
математического ожидания mX,
если для любой его реализации x(t)
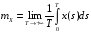 .
.
Проверка данного равенства:
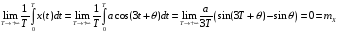 –
–
следовательно, случайный процесс X(t) эргодичен относительно математического ожидания.
Стационарный случайный процесс X(t) называется эргодическим относительно корреляционной функции kX(τ), если для любой его реализации x(t)
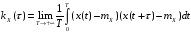 .
.
Проверка данного равенства:
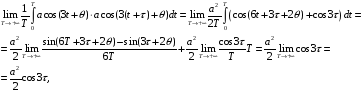
что
не совпадает с
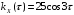 при
при
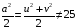 .
Таким образом, равенство выполняется
не для всякой реализации x(t)
случайного процесса X(t),
следовательно, случайный процесс X(t)
не является эргодическим относительно
корреляционной функции.
.
Таким образом, равенство выполняется
не для всякой реализации x(t)
случайного процесса X(t),
следовательно, случайный процесс X(t)
не является эргодическим относительно
корреляционной функции.
Дисперсия случайного процесса X(t) имеет вид:
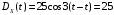 .
.
Задание №9
Дано:
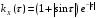
Решение:
Пусть
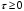 .
Тогда
.
Тогда
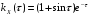 .
Имеем:
.
Имеем:
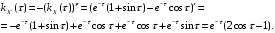
Так
как функция
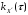 – четная, то, доопределив полученную
функцию по четности на интервале
– четная, то, доопределив полученную
функцию по четности на интервале
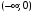 ,
получим
,
получим
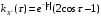 при
при
 .
.
Дисперсия
случайного процесса X(t)
равна
 .
.
Взаимная корреляционная функция имеет вид:
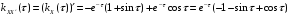 ,
,
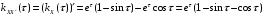 ,
,
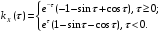
Задание №10
Дано:
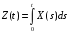 ;
;
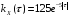 ;
;

Решение:
При
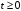 имеем:
имеем:
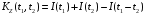 ,
где
,
где
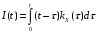 .
Тогда:
.
Тогда:
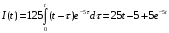 ;
;

Дисперсия случайного процесса Z(t) имеет вид:
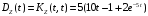 .
.
При
условии
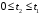 ,
взаимная корреляционная функция
случайных процессов X(t)
и Z(t)
имеет вид:
,
взаимная корреляционная функция
случайных процессов X(t)
и Z(t)
имеет вид:
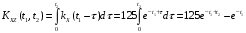 .
.
Задание №11
Дано:

Решение: Спектральная плотность имеет вид:
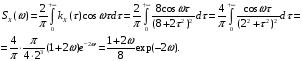 .
.
Выводы.
В ходе выполнения лабораторной работы были получены навыки нахождения различных характеристик случайных процессов, такие как математическое ожидание, дисперсия, корреляционная функция (в том числе и нормированная), спектральная плотность.
