контр.раб. выс.мат / контрольная высш.мат. вариант 26

Задача № 1.26

В первом ящике 24 детали, из которых 16 – стандартные, во втором ящике 18 деталей, 15 из них стандартные. Из каждого ящика наугад берут по две детали. Какова вероятность того, что: а) три детали будут стандартные; б) хотя бы две детали стандартные; в) ни одной стандартной детали?

Решение

а) Среди вынутых деталей три будут стандартными, если из первого ящика вынута одна стандартная и одна нестандартная деталь, а из второго ящика две стандартные детали, либо наоборот. Вероятность того, что из первого ящика вынут одну стандартную и одну нестандартную деталь:

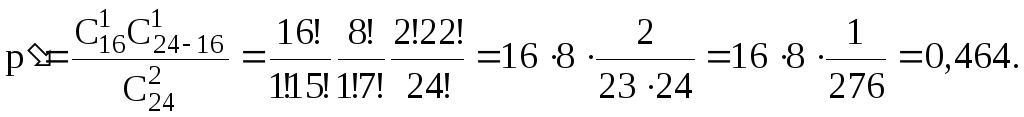
Вероятность вынуть из первого ящика две стандартных детали:

Находим аналогичные вероятности для второго ящика:

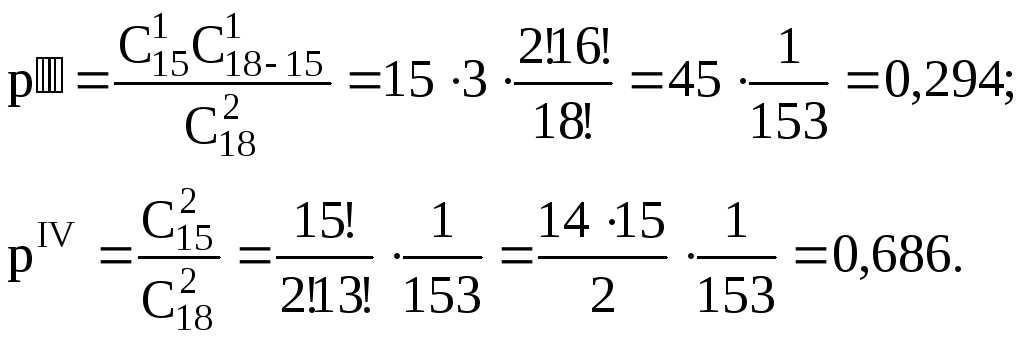
Тогда искомая вероятность того, что среди вынутых деталей будут три стандартные:

б) Вероятность того, что ноль деталей будут стандартными:

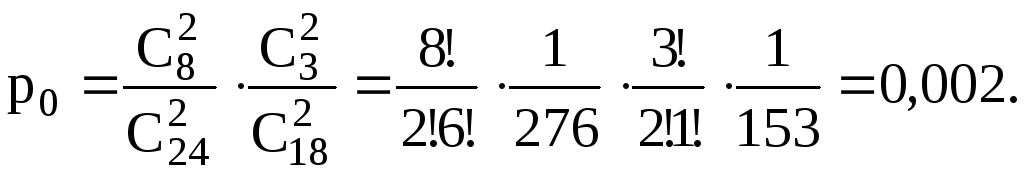
Вероятность того, что только одна деталь стандартная (она может быть извлечена как из первого, так и из второго ящика):

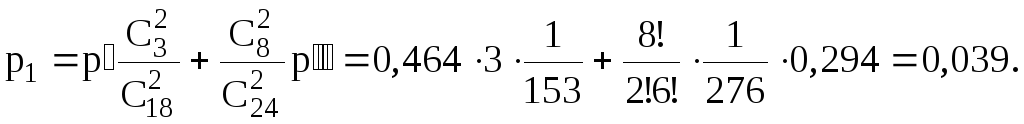
Тогда искомая вероятность того, что будет извлечено хотя бы две стандартные детали:

в) Вероятность того, что не будет извлечено ни одной стандартной детали:

Ответ: а) 0,446; б) 0,959; в) 0,002.

Задача № 2.26

Вероятность производства бракованной детали равна p. Найти вероятность того, что из взятых на проверку n деталей m бракованных.

Решение

Так как вероятность р – мала, а число n – велико, то используем формулу Пуассона. Искомая вероятность: Вычисляем:

Ответ: 0,1586.

Задача № 3.26

Охотник, имеющий n патронов, стреляет в цель до первого попадания (или пока не израсходует все патроны). Вероятность попадания при каждом выстреле равна p. Составить закон распределения СВ X – числа израсходованных патронов. Вычислить M(Х), D(X ) и σ(X ).

n=4; p=0,6.

Решение

Возможные значения СВ Х: 1; 2; 3; 4.

Находим соответствующие вероятности:

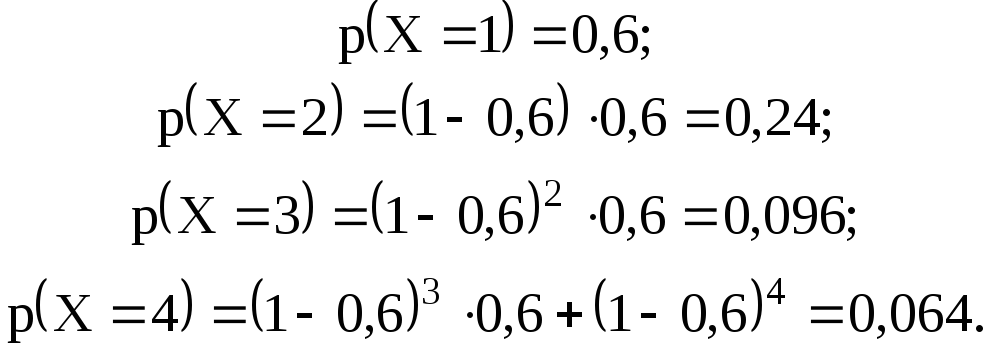
Составляем закон распределения СВ Х.

xi	1	2	3	4
pi	0,6	0,24	0,096	0,064

Проверка:

Для определения числовых характеристик СВ Х составим расчётную таблицу.

xi	pi	xipi
1	0,6	0,6	0,6
2	0,24	0,48	0,96
3	0,096	0,288	0,864
4	0,064	0,256	1,024
∑	1	1,624	3,448

Математическое ожидание:

Дисперсия:

Среднеквадратическое отклонение:

Задача № 4.26

Решение

Среднеквадратическое отклонение:

Математическое ожидание:

Плотность вероятности:

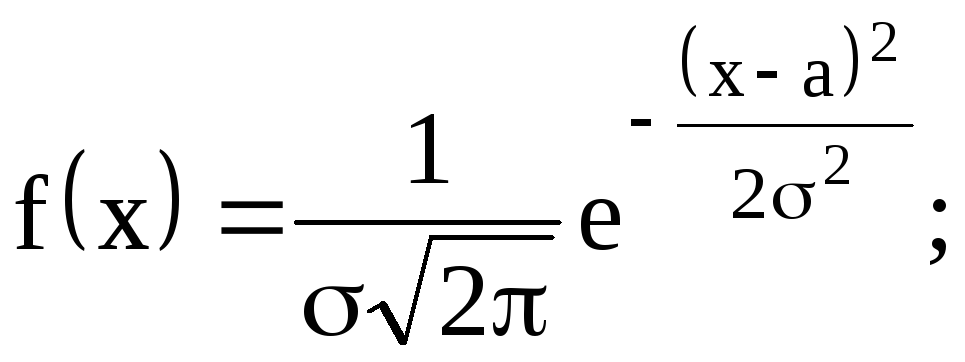
Строим график функции f(x).

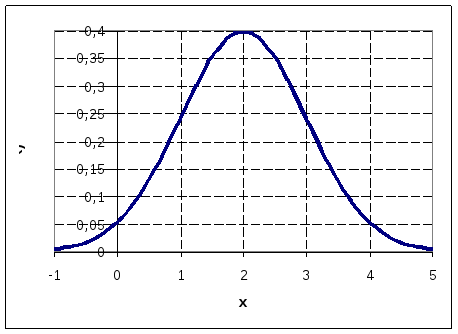
Интервал практически наиболее вероятных значений СВ Х (по правилу трёх сигм):

Находим вероятности:

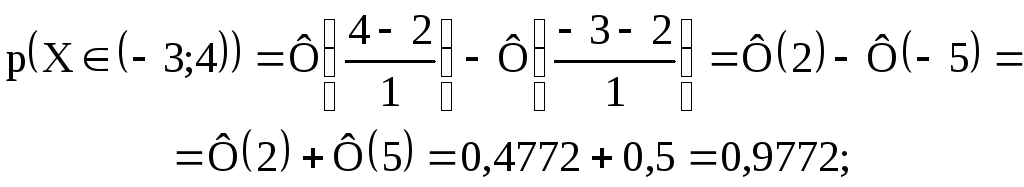
Здесь Ф(х) – функция Лапласа (задаётся таблично).

Так как , то для СВ Х вероятнее попасть в интервал , чем в интервал .

Задача № 5.26

2	4	2	0	4	2	0	5	1	1	3	0	0	2
4	3	2	1	3	0	4	5	1	2	3	3	1
5	2	0	0	2	3	2	1	2	6	2	1	3
3	1	3	1	5	4	2	3	4	3	5	5	3
2	6	0	2	1	1	3	2	3	5	3	5	2
5	1	1	1

Решение

Обозначим через x_i варианты признака X. По условию видим, что x_i принимает значения 0;1;2;3;4;5;6. Поэтому Х – дискретная СВ. Объём выборки n=70. Составляем расчётную таблицу, где на основе исходных данных заполняем первые 4 её столбца.

i	xi	ni	ni/n	F*(xi)	xini		pi		ni
1	2	3	4	5	6	7	8	9	10	11
0	0	8	0,1143	0,1143	0	0	0,0857	5,999	8	0,6674
1	1	14	0,2000	0,3143	14	14	0,2105	14,735	14	0,0367
2	2	16	0,2286	0,5429	32	64	0,2587	18,109	16	0,2457
3	3	15	0,2143	0,7572	45	135	0,2118	14,826	15	0,0020
4	4	6	0,0857	0,8429	24	96	0,1301	9,107	6	1,0600
5	5	9	0,1286	0,9715	45	225	0,0639	6,307	11	3,4921
6	6	2	0,0285	1	12	72	0,0262
∑	-	70	1	-	172	606	0,9869	-	-	5,5039

На основании столбцов 2 и 3 таблицы строим полигон частот.

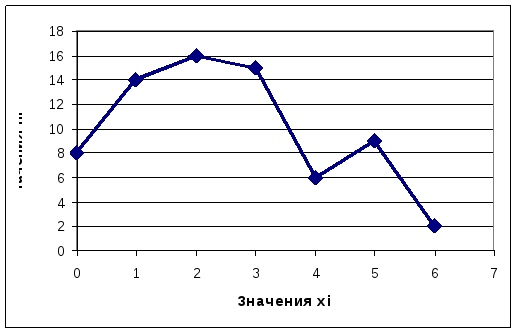
Эмпирическая функция распределения: , где n_x – сумма частот вариант, меньших х. На основании столбца 4 таблицы получаем:

Строим график эмпирической функции распределения.

F^*(x)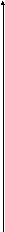

1

0 1 2 3 4 5 6 x

Заполняем пятый столбец таблицы. Также на основе имеющихся данных заполняем шестой и седьмой столбцы таблицы.

Находим числовые характеристики выборки:

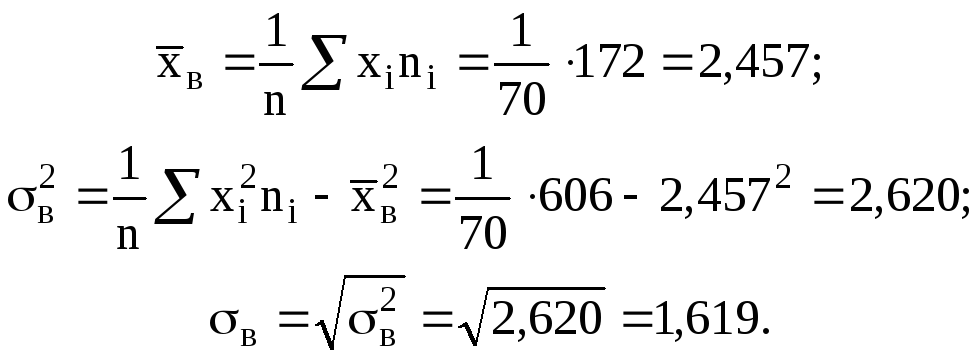
По виду полигона, а также из того, что почти совпадают, что является признаком распределения Пуассона, выдвинем гипотезу о том, что рассматриваемый признак Х распределён по закону Пуассона , где - математическое ожидание и дисперсия распределения. Пусть - математическое ожидание, тогда: . На основании этой формулы вычисляем теоретические вероятности и сводим их в столбец 8 таблицы. Сумма p_i отличается от единицы, так как она была бы равна единице, если бы .

Сравнивая графы 4 и 8, заключаем, что распределение близко к пуассоновскому.

На основании имеющихся данных заполняем столбцы 9, 10 и 11 таблицы. Причём в этих столбцах объединены два последних интервала, так как частота в каждом интервале должна быть не меньше пяти.

По таблице находим: .

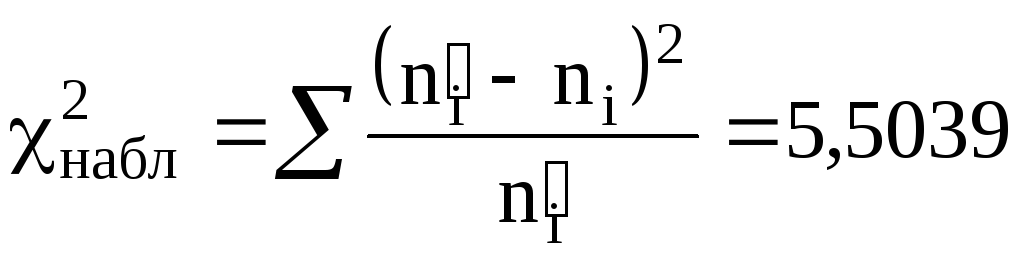Число групп в таблице с учётом объединения k=6, число параметров распределения r=1, тогда число степеней свободы . По таблице распределения Пирсона при находим критическое значение: . Так как , то принимаем гипотезу о пуассоновском распределении генеральной совокупности.

Задача № 6.26

672	668	671	671	668	672	669	673	673	666	672	673	673	663	677
669	674	670	674	672	676	671	666	662	669	674	674	669	675	670
676	674	669	664	675	672	676	668	668	678	671	671	668	667	674
671	668	672	671	671	671	669	661	674	665	670	672	665	674	675
667	673	678	673	671	675	673	671	672	668	667	669	669	677	663
671	674	667	668	664	674	669	667	674	666	674	668	681	674	672
671	666	666	670	669

Решение

Так как повторяющихся значений довольно немного, то этот признак следует отнести к непрерывным. Объём выборки: n=95. Строим вариационный ряд, то есть располагаем исходные данные в порядке возрастания (в таблице 1 варианты в порядке возрастания расположены по столбцам).

Таблица 1

661	667	669	671	672	674	677
662	667	669	671	672	674	677
663	667	669	671	672	674	678
663	668	669	671	673	674	678
664	668	669	671	673	674	681
664	668	669	671	673	674
665	668	669	671	673	674
665	668	670	671	673	674
666	668	670	671	673	675
666	668	670	672	673	675
666	668	670	672	674	675
666	668	671	672	674	675
666	669	671	672	674	676
667	669	671	672	674	676
667	669	671	672	674	676

По формуле Стерджесса находим длину интервала варьирования:

Начало первого интервала находим по формуле:

К а₀ прибавляя последовательно h, находим начала остальных интервалов и конец последнего интервала. Далее на основании таблицы 1 подсчитываем количество вариант в каждом интервале. Результаты сводим в столбец 2 и 3, 4 таблицы 2. Здесь x_i – середины интервалов.

Таблица 2