Применение математической статистики при обработке результатов анализа

Ошибки измерений. Во всякой экспериментальной работе большое значение имеет точность измерений, воспроизводимость и правильность результатов анализа. Опыт показывает, что любая измеряемая величина имеет свою ошибку; это обусловлено несовершенством приборов, их ограниченной точностью, влиянием внешних условий, потерей вещества, загрязнениями, неправильно проведенными записями и пр.

Кроме того, при измерениях могут появляться ошибки от ряда причин, природа которых остается неизвестной. Поэтому в результате эксперимента аналитик всегда устанавливает только приближенное значение определяемой величины, но никогда не может получить истинного ее значения . Вследствие этого измеряемая величина имеет некоторую ошибку, величину которой принято определять как абсолютную и относительную ошибку.

Абсолютной ошибкой М измеряемой величины называют разницу между полученным результатом измерения X и истинным (или более достоверным) значением А определяемой величины:

М = А - X, (97)

Абсолютную ошибку определяют в абсолютных единицах, ее размерность отвечает размерности измеряемой величины.

Относительной ошибкой V измеряемой величины называют отношение абсолютной ошибки М к точному значению А определяемой величины:

(1)

Но так как истинное значение измеряемой величины неизвестно и абсолютная ошибка М очень мала по сравнению с величинами Л и X, то в формуле (1) величину А можно заменить очень близкой к ней величиной X. Тогда отно­сительная ошибка будет определяться по формуле

(2)

откуда

(3)

Относительная ошибка, как видно из формулы (2), является отношением двух величин одной и той же размерности, поэтому относительные ошибки — всегда безразмерные величины. Относительную ошибку, как правило, выражают в процентах

(4)

В связи с этим возникает необходимость оценить степень приближения определяемой величины к истинному ее значению, иными словами, дать оценку точности полученных данных эксперимента, а в некоторых случаях выяснить и устранить причины, обусловливающие появление ошибок.

Цель будет достигнута, если для обработки экспериментальных данных применить методы математической статистики, сформулированные в теории ошибок.

Все ошибки разделяют на систематические, случайные и грубые (промахи).

Систематические сшибки зависят от неправильных показаний измерительных приборов, неправильно градуированных приборов, мерных колб, пипеток, бюреток, невыверенных разновесов и др. Систематические ошибки должны быть устранены. Для этого перед работой все приборы необходимо прокалибровать, неисправные заменить на исправные и т. д. В показания выверенных приборов следует внести соответствующие поправки.

Случайные ошибки возникают от различных помех, несовершенства органов чувств экспериментатора и других случайных причин. Ограниченная точность приборов, изменение условий, при которых проводится опыт (особенно это имеет значение при параллельных определениях), также приводят к возникновению случайных ошибок. Устранить их при измерениях невозможно, однако, поль­зуясь методом теории ошибок, можно уменьшить их влияние на результаты анализа и более точно установить вероятную ошибку в этих результатах.

Грубые ошибки в основном связаны с субъективными свойствами экспериментатора: невнимательностью и неряшливостью, занятием посторонними делами во время работы и др. Это приводит к неверным отсчетам, неправильным записям. При обработке результатов анализа грубые ошибки во внимание не при­нимают — их отбрасывают.

Метод математической статистики, применяемый для обработки результатов измерений, вполне оправдал себя в ряде областей науки. Однако в области химического анализа его применение еще недостаточно, хотя в этом имеется необходимость.

Известно, что анализ вещества сопровождается рядом массовых однотипных операций; это: взятие навески, растворение, градуировка мерной посуды, титрование, измерение силы тока и др. Все эти операции выполняются различными приборами, среди которых можно выделить совокупность таких однотипных приборов, как гальванометры, аналитические весы, микропипетки и многие другие. Поэтому работа аналитика относится к таким процессам, к которым можно применять методы математической статистики для обработки результатов эксперимента.

Широкое использование методов математической статистики для обработки экспериментальных данных, а также для оценки аналитических данных в любой лаборатории приносит очень большую пользу.

Нормальное распределение. Результаты каждого анализа представляют собой сумму большого числа взаимно независимых слагаемых (процессов взвешивания, растворения, осаждения и др.), которые подвергаются воздействию многообразных факторов. Поэтому можно считать, что случайные ошибки при всех химических анализах подчиняются закону нормального (гауссовского) распределения вероятностей и описываются уравнением:

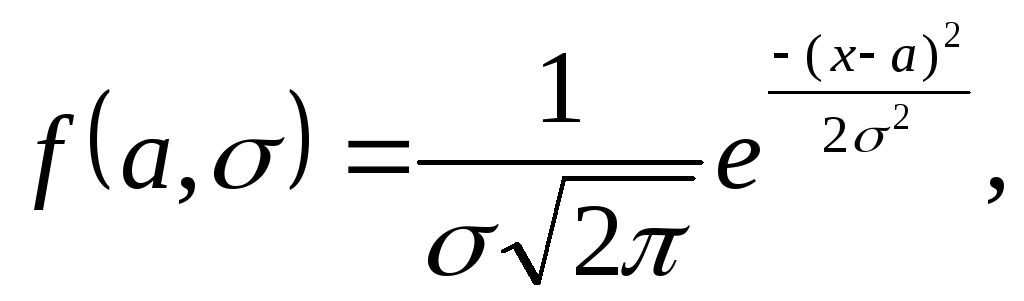(5)

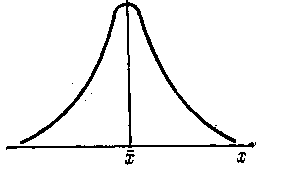
Рис. 1. Кривая нормаль­ного распределения.

где а — истинное значение определяемой ве­личины; х — значение, полученное при данном измерении; ² — дисперсия;  — среднее квадратическое отклонение;  и е — известные математические константы:  = 3,1416..., е — основание натуральных логарифмов (е = =2,1783).

Данная формула включает истинное зна­чение определяемой величины а и выведена на основе предположения, что число измере­ний велико.

Кривая нормального распределения (рис. 1) симметрично распределяется относительно ординаты, проходящей через точку х-х на оси абсцисс, и асимптотически приближается к оси абсцисс.

В практике обычно пользуются нормированным распределением для удобства сравнения различных распределений, данные которых выражают в единой форме. При этом частоты или вероятности выражают в относительных числах, в долях единицы или процентах, приняв полную вероятность за единицу или за 100%, а значения варьирующего признака — не в именованных единицах, а в так называемых нормированных отклонениях, долях среднего квадратического отклонения , которые обозначаются буквой t.

Нормированные отклонения определяются по формуле:

Нормирование сводится к тому, что начало координат переносят в центр распределения х, а по оси абсцисс откладывают отклонения х от х, выраженное в долях , т. е.

.

На оси ординат откладывают частоты в долях единицы или процентах.

При таком способе получения кривых нормального распределения, не­смотря на большие различия их по форме, площадь, образуемая ими с осью абсцисс, будет для них всегда равна единице при любых значениях и  .

Отсюда следует, что форма кривой нормального распределения зависит от среднего квадратического отклонения . Если значения среднего квадратического отклонения малы, то кривая имеет иглообразную форму, а если они больше, кривая становится пологой.

На рис. 173 приведены три кривые нормального распределения резуль­татов измерения с равными х и различными значениями , т. е. ₁ = 1; ₂ = 2; ₃ = 4, подтверждающие это. Наблюдаемые отклонения варьирующего приз­нака от х влево и вправо определяются величиной  и в основном укладываются в границах трех квадратических отклонений ±3 или трех нормированных отклонений ±3t, потому что t выражено в . Из рис. 174 видно, что в преде­лах укладывается основная масса всех наблюдений (68,3%, т. е. около²/з). Поэтому  называется основным отклонением. В пределах находится 95,5%, а в пределах— 99,7% всех наблюдений, т. е. укладываются почти все наблюдаемые отклонения вариационного ряда. Продолжение кривой за пределыпрактического значения не имеет, так как вероятность встре­тить значение варьирующего признака, превышающегона , равна только 0,3%, т. е. 3 наблюдения на 1000 могут отклоняться больше чем на .

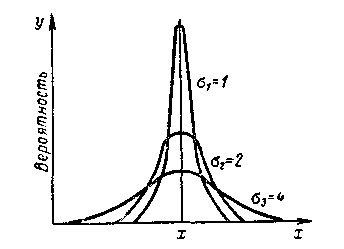
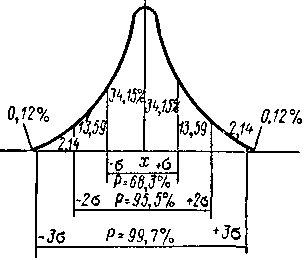
Рис. 2. Кривая нормального рас- Рис. 3. Теоретические полигоны

пределенияс различными значения- вариаций, включающие число слу-

ми сигмы. чаев в пределах:

В практической работе считают возможным пользоваться вероятностями, которые соответствуют величинам ±2 (±2t) и ±3 (±3 t). Вероятность для: ±2 (±2 t) выражают округленной величиной 0,95, или 95%, а для: ±3 (±3t) — 0,99, или 99%. Эти вероятности называют доверительными вероятностями или надежностями, и обозначают ; это значения, которыми можно уверенно пользоваться.

В работе при использовании вероятности 0,95 (95%) риск сделать ошибку составляет 0,05 (5%), или 1 раз на 20, а при вероятности 0,99 (99%) возможность ошибиться составляет 0,01 (1%), или 1 раз на 100. Величины 0,05 (5%) и 0,01 (1%) получили название уровней значимости.

Выбор в работе доверительной вероятности, т. е. надежности, или уровня значимости для тех или иных исследований подсказывается практическими соображениями и возможностями, а также ответственностью выводов. В аналитической работе обычно принимают двусигмовые пределы за допустимые откло­нения, а величину ±2 называют максимальной допустимой ошибкой. Рекомен­дуется пользоваться доверительной вероятностью, т. е. надежностью  = 0,95.

Закон нормального распределения вероятностей применим для большого числа (п) измерении или наблюдений так называемой генеральной совокупности явлений. Установлено, что нормальное распределение применимо для наблюде­ний при п > 20. В связи с этим классическая теория ошибок, основанная на нормальном распределении, неприменима для обработки малого числа измере­ний.

С начала XX в. в математической статистике стало разрабатываться новое направление, которое получило название статистики малых выборок, или микро-статистики. Очень большое практическое значение для малых выборок получило открытое в 1908 г. английским химиком и статистиком Гассетом t-распределение, получившее название распределения Стьюдента (Стьюдент — псевдоним Гассета).

Распределение Стьюдента зависит от числа степеней свободы, по которым определяется среднее квадратическое отклонение, т. е. выборочная дисперсия. Число степеней свободы обозначают буквой k и рассчитывают по формуле k = п — 1. Соотношение между кривыми нормального распределения и кривыми t-распределения для числа степеней свободы k = п — 1 = 1 и k = п — 1 = 5 показано на рис. 5. Как видно из рисунка, кривые t-распределения по форме напоминают кривые нормального распределения, но при малых значениях числа степеней свободы k = п — 1 они очень медленно сближаются с осью абсцисс.

Как показали Комарь и др., для оценки экспериментального материала, полученного в аналитических лабораториях (где экспериментатор в силу специфики работы делает сравнительно ограниченное число измерений), можно применять методы статистической обработки экспериментальных данных, основанных на t-распределении для малых выборок.

В статистическом анализе при обработке экспериментального материала проводят четкое разграничение между параметрами малых выборок и параметрами генеральной совокупности. Греческими буквами обозначают все пара­метры генеральной совокупности, а латинскими — параметры милых выборок.

Для обработки результатов химиче­ского анализа с целью оценки точности метода и качества выполняемых анали­тических работ (воспроизведение, правильность) с успехом можно применять метод математической статистики, разработанный для малого числа наблюдений. При этом полученную систему наблюдений рассматривают как случайную выборку из некоторой гипотетической ге­неральной совокупности явлений.

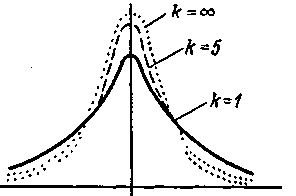
Рис. 5. Соотношение между нор­мальным распределением k =  и t-распределением для k = 1 и k =5.

Оценка точности измерений. Результаты химических анализов являются приближенными числами. Нахождение наиболее вероятного их значения — одна из важнейших задач при обработке результатов анализа [2, 5—13].

Под вероятностью какого-либо явления принято понимать отношение числа случаев, благоприятствующих этому явлению, к числу всех случаев, образующих рассматриваемую группу. При этом считается, что вероятность появления всех случаев одинакова, поэтому нет оснований полагать, что какой-нибудь из случаев имеет больше, а другой меньше шансов осуществиться.

Например, в коробке находится 15 шаров, из них 8 белых, 4 синих и 3 желтых. Вероятность вынуть из коробки шар того или другого цвета будет соответственно равна: для белого — ⁸/₁₅, для синего — ⁴/₁₅ и для желтого — ³/₁₅. Но из этой коробки нельзя вынуть черный шар, ибо его здесь нет; поэтому вероятность такого случая равна нулю. Если в коробке будут все шары синего цвета, то вероятность вынуть шар синего цвета равна единице.

Сумма вероятностей всех событий в рассматриваемой группе равна единице, иногда вероятности отдельно или их сумму выражают в процентах.

На основании закона нормального распределения случайных ошибок показано, что арифметическое среднее из результатов всех измерений является наиболее вероятным значением измеряемой величины и определяется по фор­муле:

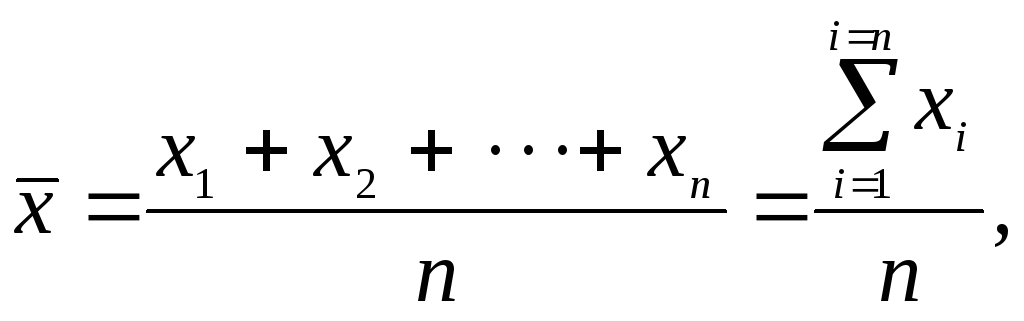
где x₁, x₂, … , х_п — результаты отдельных измерений; п — число параллельных измерений; — среднее арифметическое значение определяемой величины, оно Принимается за приближенное значение истинного числа и записывается

В случаях, когда для оценки пользуются средними арифметическими данными, имеющими различную достоверность, одним данным придают большее значение, другим — меньшее. Например, получены данные результатов ана­лиза 0,25% и 0,31%; допустим, что первому результату придается большее значение, т. е. больший нес, например 2, а второму меньший — 1. Тогда среднее арифметическое вычисляют так:

Но этим приемом определения среднего арифметического следует пользоваться с чрезвычайно большой осторожностью, так как он может внести заметную субъективную ошибку.

Отклонение случайной измеряемой величины от среднего арифметического принято в теории ошибок называть дисперсией или рассеиванием.

Дисперсия в достаточной степени характеризует воспроизводимость метода. Установлено, что чем меньше точность измерений, тем больше дисперсия, и наоборот — при более точных измерениях дисперсия мала.

Дисперсия в малых выборках обозначается символом S² и вычисляется по формуле:

(6)

Корень квадратный из величины выборочной дисперсии называется стандартным отклонением или средним квадратическим отклонением (S) отдельного определения от средней арифметической. Оно вычисляется по формуле:

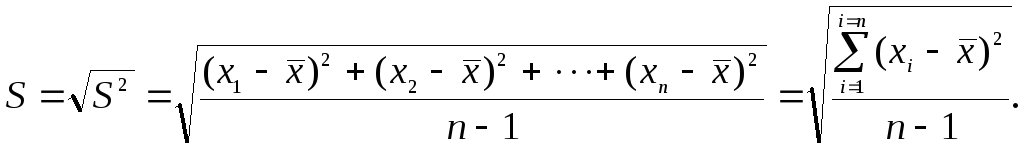(7)

При оценке точности полученных результатов анализа вычисляют выборочную дисперсию средней квадратической S-. Для этого пользуются формулой

(8)

Квадратный корень из этой величины называется средней квадратической ошибкой среднего арифметического и вычисляется по формуле:

(9)

Точность прямого измерения характеризуется величиной , которая равна абсолютной величине разности между средней арифметическойк и истинным значением измеряемой величины а. Его рассчитывают по формуле:

(10)

или

(11)

где  — доверительная вероятность, или надежность (в практической работе больше всего пользуются надежностью 0,95, реже — 0,99 и еще реже — надежностью 0,999); t_,_k — коэффициент нормированных отклонений при малой выборке, который зависит от п и . Числовые значения t_,_k для различных  и k = п — 1 приведены в табл. 1, где п — число измерений, a k — число сте­пеней свободы.

Таблица 1

Значения t_,_k для различных а и k

k				k	
	0,95	0,99	0,999		0,95	0,99	0,999
1	2	3	4	1	2	3	4
1	12,706	63,657	636,619	18	2,103	2,878	3,922
2	4,303	9,925	31,598	19	2,093	2,861	3,883
3	3,182	5,841	12,941	20	2,088	2,845	3,850
4	2,776	4,804	8,610	21	2,080	2,831	3,819
5	2,571	4,032	6,859	22	2,074	2,819	3,792
6	2,447	3,707	5,959	23	2,069	2,807	3,767
7	2,365	3,499	5,405	24	2,064	2,797	3,745
8	2,306	3,355	5,041	25	2,060	2,787	3,725
9	2,262	3,250	4,781	26	2,058	2,779	3,707
10	2,228	3,169	4,587	27	2,052	2,771	3,690
11	2,201	3,106	4,487	28	2,048	2,783	3,674
12	2,179	3,055	4,318	29	2,045	2,756	3,659
13	2,160	3,012	4,221	30	2,042	2,750	3,648
14	2,145	2,977	4,140	40	2,021	2,704	3,551
15	2,131	2,947	4,073	60	2,000	2,660	3,460
16	2,120	2,921	4,015	120	1,980	2,617	3,373
17	2,110	2,898	3,965	~	1,980	2,576	3,291

Для характеристики точности метода кроме рассчитывают его вероятную относительную ошибку по формуле

(12)

или

(13)

где t_,_k — множитель, зависящий от надежности и от числа степеней свободы k = п — 1; — средняя арифметическая из п числа определений.

Для характеристики относительной пестроты или выравненности варьи­рующего признака в изучаемом явлении определяют коэффициент вариаций или изменчивости.

Коэффициентом вариации (изменчивости) называют отношение среднего квадратического отклонения, выраженного в процентах, к среднему арифмети­ческому. Его обозначают V и вычисляют по формуле

(14)

Чем больше V, тем относительно больше пестрота и меньше выравненность изучаемых явлений, и наоборот.

Коэффициент вариации, будучи отвлеченным числом, выраженным в процентах, дает возможность сравнивать варьирование признаков разной размерности.

Ё При небольшом числе измерений кроме определения точности прямого измерения, т. е. _, вычисляют еще доверительный интервал (предел), или интервальное значение измеряемой величины. Интервальным значением или до­верительным пределом называют границы, в пределах которых с_надежностью  находится__истинное__значение измеряемой величины а.

Доверительный предел измеряемой величины рассчитывают по формуле

(14)

и

(15)

или

(16)

В теории ошибок установлено, что, пользуясь этими уравнениями, можно достаточно точно оценить приближенное равенство .

При малом числе измерений, кроме доверительного предела (или так называемого интервального значения) измеряемой величины требуется вычислить и приближенно оценить значение стандартного отклонения  для генеральной совокупности. При этом допускают, что стандартное отклонение для генеральной совокупности  приближенно равно средней квадратической ошибке отдельного определения S при малом числе измерений, т. е.   S.

В этом случае интервальное значение  будет вычисляться так:

(17)

где — точность стандартного отклонения, найденная при надежности  и числе степеней свободы k = п — 1 по формуле — множи­тель, который зависит от надежности и числа степеней свободы k = п — 1 (табл. 2); S — среднее квадратическое отклонение отдельного определения. При вычислении и оценке границ  допускают, что для q > 1 левая дове­рительная граница интервального значения  равна нулю. Тогда формула для расчета и оценки стандартного отклонения будет иметь вид:

0< <S+_. (18)

Если истинное число а известно и обработка экспериментальных данных показывает, что

(19)

значит, в измерениях допущена систематическая ошибка Е . Доверительный предел ее может быть найден по формуле:

(20)

Следовательно, полученные после статистической обработки экспериментальных данных значения позволяют полностью определить точность, правильность и воспроизводимость проводимых наблюдений.

Таблица 2