
Простые числа №1
.doc§2 Простые числа.
п.1 Простые и составные числа.
Сколько делителей может иметь натуральное
число? У числа 1 только один делитель.
Всякое натуральное
![]() имеет
два делителя: 1 и само число а. Есть
числа, которые не имеют других делителей.
имеет
два делителя: 1 и само число а. Есть
числа, которые не имеют других делителей.
Определение. Натуральное число р называется простым, если оно имеет ровно два делителя: 1 и р.
Определение. Натуральное число, а называется составным, если кроме 1 и а у него есть еще, хотя бы один делитель.
Замечание. Число 1 не относится ни к составным, ни к простым.
Множество N можно разбить на три подмножества.
-
1 — число, имеющее один делитель.
-
Простые числа, имеющие ровно два делителя.
-
Составные числа, имеющие по меньшей мере три делителя.
Выпишем несколько первых простых чисел:
2, 3, 5, 7, 11, 13, 17 …
Бесконечно ли эта последовательность, или можно перечислить все простые числа? Ответ был известен еще Евклиду.
Теорема. (Евклида)
Множество простых чисел бесконечно.
Доказательство. “![]() ”Пусть
”Пусть
![]() —
множество всех простых чисел, где
—
множество всех простых чисел, где
![]() —
последнее (наибольшее) простое число.
—
последнее (наибольшее) простое число.
Составим число
![]() .
Очевидно,
.
Очевидно,
![]() ,
значит, N—составное.
,
значит, N—составное.![]() делится
на какое-то из простых, например, на
делится
на какое-то из простых, например, на
![]() .
Но тогда, по свойствам делимости, 1
делится на
.
Но тогда, по свойствам делимости, 1
делится на
![]() ,
что невозможно.
,
что невозможно.
■
Рассмотрим некоторые элементарные свойства простых чисел.
1. Пусть
![]() —
наименьший делитель натурального числа
а.
—
наименьший делитель натурального числа
а.
Тогда p—простое число.
Доказательство. Пусть d—некоторый
делитель числа p.
![]()
Но p—наименьший
делитель
![]() или
или
![]() p—простое.
p—простое.
■
2. Пусть
![]() —
наименьший делитель составного числа
а.
—
наименьший делитель составного числа
а.
Тогда
![]()
Доказательство. а— составное, значит
![]()
По условию
![]()
■
3. Пусть а — натуральное число, p — простое число.
Тогда а делится на p, либо а и p взаимно просты.
Доказательство. Пусть
![]() .
D — делитель простого
.
D — делитель простого
![]() или
или![]()
Если d=1, то а и p взаимно просты.
Если d=p, то а делится на р.
■
4. Пусть p—простое число, произведение аb делится на p, тогда а делится на p или b делится на р.
Доказательство. Если а не делится на p, то по свойству 3 НОД(а, p)=1.
Но тогда, по свойству 2 взаимно простых чисел, b делится на р.
■
Замечание 1. Свойство 4 легко обобщать
по индукции: если произведение
![]() делится
на простое p, то найдется
множитель
делится
на простое p, то найдется
множитель
![]() ,
который делится на р.
,
который делится на р.
Замечание 2. Если произведение
![]() делится на простое p,
причем все сомножители
делится на простое p,
причем все сомножители
![]() —
простые числа, то хотя бы один из
сомножителей равен р.
—
простые числа, то хотя бы один из
сомножителей равен р.
Для составления списка простых чисел, не превосходящих заданного числа N, используют алгоритм, который называют “решето Эратосфена”.
Выпишем натуральные числа от 2 до N.
![]()
Число 2 — простое. Вычеркнем из списка все числа кратные 2 (кроме 2). Первое из оставшихся—число 3, будет простым. Вычеркнем из списка все числа кратные 3 (кроме числа 3). Первое из оставшихся—число 5, будет простым. Затем вычеркнем все числа, кратные 5 (кроме числа 5) и так далее.
Алгоритм остановится, когда не вычеркнутое
число станет больше, чем
![]() .
Действительно, по свойству 2, все составные
числа в нашем списке имеют делитель
.
Действительно, по свойству 2, все составные
числа в нашем списке имеют делитель
![]() .
Значит, они уже вычеркнуты.
.
Значит, они уже вычеркнуты.
Все остальные числа — простые.
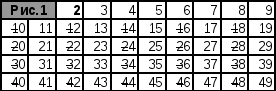
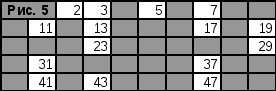
Пример. Найти все простые числа на промежутке от 2 до 100.
Решение. Вычеркнем (выделим) числа, кратные 2 (рис. 1).
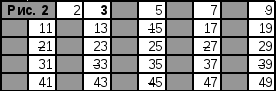
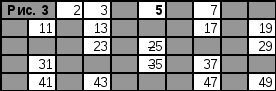
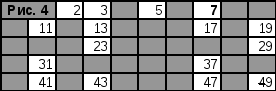
Далее, вычеркнем числа кратные 3 (рис.2), кратные 5 (рис. 3) и кратные 7 (рис. 4).
Следующее простое число
![]() все
остальные числа — простые (рис. 5).
все
остальные числа — простые (рис. 5).
Замечание. Если p
— первое, не вычеркнутое число, то все
числа меньше
![]() уже вычеркнуты.
уже вычеркнуты.
![]() Вычеркивать кратные числу p
можно начинать с
Вычеркивать кратные числу p
можно начинать с
![]() .
.
п. 2 Факторизация.
Составное число 495 имеет делитель 5,
значит
![]() .
Второй сомножитель также число составное
.
Второй сомножитель также число составное
![]() .
Продолжая процесс, можно исходно число
разложить на множители
.
Продолжая процесс, можно исходно число
разложить на множители
![]()
Определение. Факторизацией составного числа N называется разложение N на простые множители.
Самый очевидный способ факторизации
числа N сводится к
перебору всех возможных простых
делителей,
![]() .
.
Пример. Разложить на множитель число 323.
Заметим, что
![]() .
Значит, делитель нужно искать среди
простых чисел
.
Значит, делитель нужно искать среди
простых чисел
![]() .
Перебирая их по очереди находим, что
.
Перебирая их по очереди находим, что
![]()
Пример. Доказать, что 919 — простое число.
Так как
![]() ,
то наименьший простой делитель не
превосходит 29. Проверкой убедимся, что
919 не делится на простые числа
,
то наименьший простой делитель не
превосходит 29. Проверкой убедимся, что
919 не делится на простые числа
![]() .
.
![]() —
простое число.
—
простое число.
Для больших натуральных чисел рассмотренный способ неэффективен. Многие математики искали более простые способы факторизации, требующие меньшего объема вычислений.
I. Метод Ферма.
Пусть N — данное число,
![]() .
Образуем числа
.
Образуем числа
![]()
Если одно из них окажется точным
квадратом, то получим равенство
![]() ,
или
,
или
![]() .
.
Перебор следует вести в плоть до значения
![]() .
(В этом случае
.
(В этом случае
![]() и
и
![]() ).
Если точный квадрат
).
Если точный квадрат
![]() не
встретился, то N —
простое число.
не
встретился, то N —
простое число.
Пример. Разложить на множители N=9271.
Имеем
![]() ,
значит m=97. вычислим
последовательно:
,
значит m=97. вычислим
последовательно:
![]() .
.
Итак,
![]() .
.
II. Метод Эйлера.
Эйлер предложил записывать число N
в виде суммы
![]() ,
где d — специально
подобранный множитель такой, что НОД
(x, yd)=1.
величина d зависит от
вида числа N. Так, если
N=4k+1,
то d=1, если N=6k+1,
то d=3 и т.д. Всего Эйлер
указал 65 множителей d
для разных видов N.
,
где d — специально
подобранный множитель такой, что НОД
(x, yd)=1.
величина d зависит от
вида числа N. Так, если
N=4k+1,
то d=1, если N=6k+1,
то d=3 и т.д. Всего Эйлер
указал 65 множителей d
для разных видов N.
Если N представлено
в виде
![]() двумя способами (с одним и тем же d),
то N можно разложить
на множители.
двумя способами (с одним и тем же d),
то N можно разложить
на множители.
Например, пусть
![]()
Тогда
![]() ,
где НОД (u,v)=1.
,
где НОД (u,v)=1.
Получаем систему:
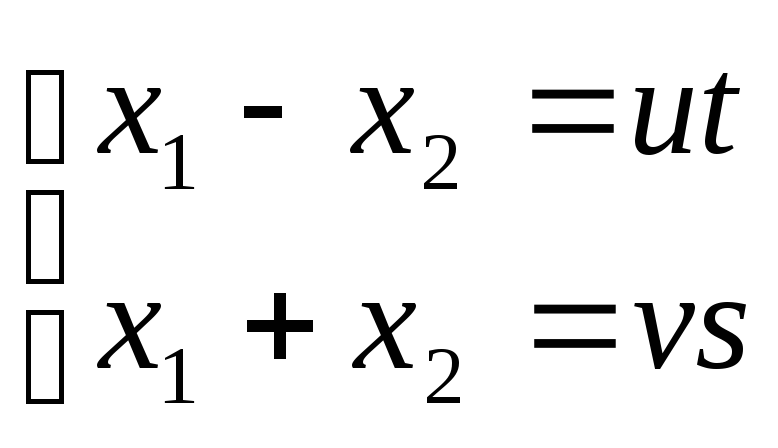 и
и
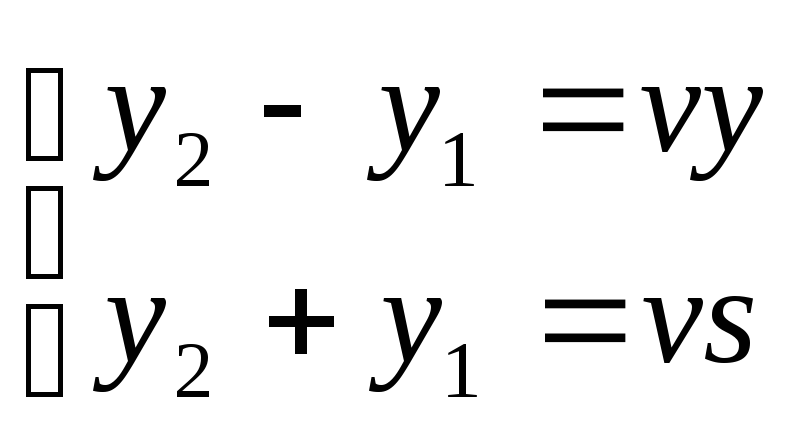
решая которые, находим:
![]() .
.
Пример. Разложить на множители N = 2197.
Имеем
![]()
Отсюда, u=2, v=3, t=10, s=24.
![]() .
.
III. Ряд приемов основан на простых
алгебраических тождествах. Например,
теорема Софии Жермен утверждает, что
![]() —
составное число.
—
составное число.
Это следует из того, что
![]() и при N>1 оба множителя
больше 1.
и при N>1 оба множителя
больше 1.
Последние десятилетия поиск новых эффективных алгоритмов факторизации слал одной из самых актуальных задач теории чисел. Причиной тому послужила разработка криптографических алгоритмов с открытым ключом, дешифровка которых требует факторизации больших составных чисел.
п.3. О формулах, генерирующих простые числа.
Долгое время математики пытались найти
формулу , позволяющие вычислить сколько
угодно большое простое число. Наибольшую
известность получила формула Мерсенна.
![]() и
числа Ферма
и
числа Ферма
![]() .
.
Определение.
![]() —
числа Мерсенна.
—
числа Мерсенна.
Для составных значений
![]() число
число
![]() делится на
делится на
![]() и
значит, не будет простым.
и
значит, не будет простым.
Пусть N — простое
число. Тогда,
![]() —
простые числа.
—
простые числа.
Но уже
![]() ,
таким образом, простота числа p
не гарантирует простату
,
таким образом, простота числа p
не гарантирует простату
![]() .
.
Простыми оказались числа Мерсенна при
![]() .
.
Простоту числа
![]() (записываемого 139 цифрами) доказал в
1876 году французский математик Э. Люка.
(записываемого 139 цифрами) доказал в
1876 году французский математик Э. Люка.
Дальнейший поиск простых чисел Месенна продолжился с помощью вычислительной техники.
Наиболее известное (на 2011 год) простое
число является 46–м числом Мерсенна.
Это
![]() .
Для его записи требуется около 13 миллионов
цифр.
.
Для его записи требуется около 13 миллионов
цифр.
Основой для вычислительных алгоритмов
служит критерий простоты чисел
![]() ,
указанный Люка в 1878 году и усовершенствованный
Лемером в 1930.
,
указанный Люка в 1878 году и усовершенствованный
Лемером в 1930.
Критерий Люка – Лемера.
Число
![]() простое тогда и только тогда, когда в
рекуррентной последовательности
простое тогда и только тогда, когда в
рекуррентной последовательности
![]() член
член
![]() делится на
делится на
![]() .
.
На сегодняшний день неизвестно, конечно или бесконечно множество чисел Мерсена.
Определение.
![]() — числа Ферма.
— числа Ферма.
Первые члены последовательности являются
простыми числами:
![]()
Ферма предположил (1650), что все числа
такого вида будут простыми. Однако Эйлер
показал (1739), что
![]() .
.
В настоящее время неизвестно, имеются
ли другие простые числа Ферма при
![]() .
.
С помощью чисел Ферма можно получить другое доказательство теоремы Эвклида.
Теорема (Пойа).
Любые два числа Ферма взаимно просты.
Доказательство. Пусть
![]() и
и
![]() —
произвольные числа Ферма.
—
произвольные числа Ферма.
Покажем, что
![]() делится на
делится на
![]() .
В самом деле,
.
В самом деле,
![]() делится на х+1, т.е. на
делится на х+1, т.е. на
![]() .
.
Пусть m — общий делитель
![]() и
и
![]() .
Тогда
.
Тогда
![]() и так как
и так как
![]() ,
значит,
,
значит,
![]() .
Но числа Ферма нечетные
.
Но числа Ферма нечетные
![]()
■
Следствие. Простых чисел бесконечно много.
Доказательство. каждое из
![]() имеет нечетный делитель, который не
делит остальные числа Ферма следовательно,
есть по меньшей мере N
простых нечетных чисел,
имеет нечетный делитель, который не
делит остальные числа Ферма следовательно,
есть по меньшей мере N
простых нечетных чисел,
![]() простых
чисел бесконечно много.
простых
чисел бесконечно много.
■
Замечание. Простые числа Ферма
неожиданно появляются в задаче о
построении правильного N–угольника
с помощью циркуля и линейки. Гаусс
доказал, что построение возможно тогда
и только тогда, когда
![]() ,
где
,
где
![]() —
простые числа Ферма.
—
простые числа Ферма.
Неоправдавшиеся предположения о простоте
чисел
![]() и
и![]() побудили ученых искать другие формулы,
значения которых были бы только простые
числа, или хотя бы содержали бесконечно
много простых значений.
побудили ученых искать другие формулы,
значения которых были бы только простые
числа, или хотя бы содержали бесконечно
много простых значений.
Эйлер обратил внимание на многочлены:
![]() ,
задающий простые числа при
,
задающий простые числа при![]() и
и
![]() ,
принимающий простые значения при
,
принимающий простые значения при
![]() .
.
Позднее была доказана следующая теорема.
Теорема (Гольдбах).
Никакой многочлен
![]() с
целыми коэффициентами не может принимать
простые значения
с
целыми коэффициентами не может принимать
простые значения
![]() при
всех
при
всех
![]() .
.
Доказательство. Пусть
![]() ,
пусть
,
пусть
![]() —
простое число.
—
простое число.
Тогда по формуле Тейлора:
![]() .
.
Все коэффициенты
![]() —
целые числа
—
целые числа
![]() делится
на р.
делится
на р.
Если попробовать, чтобы значения
![]() были
простыми, то
были
простыми, то
![]() при
всех целых t, но это
противоречит тому, что
при
всех целых t, но это
противоречит тому, что
![]() .
.
■
