
- •1. Задачи, приводящие к понятию определенного интеграла. Определение определенного интеграла.
- •2. Теорема существования определенного интеграла. Свойства определенного интеграла.
- •3. Теорема о связи определенного и неопределенного интегралов. Формула Ньютона-Лейбница.
- •4. Замена переменной в ои.
- •5. Интегрирование по частям в ои.
- •6. Несобственные интегралы по бесконечному промежутку интегрирования
- •7. Несобственные интегралы от ф-й, терпящих бесконечный разрыв
- •8. Применение определенных интегралов для выч. Площадей
- •9. Применение определенного интеграла для выч. Длин дуг
- •10. Применение определенного интеграла для выч. Объемов тел
- •11. Задачи приводящие к дифферинциальным уравнениям. Основныепонятия о дифференциальных уравнениях.
- •12. Дифференциальные уравнения первого порядка. Поле направлений. Изоклины. Задача Коши. Теорема Коши.
- •13. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка.
- •14. Линейные дифференциальные уравнения первого порядка и уравнения Бернулли. Общая схема решения дифференциальных уравнений первого порядка.
- •15. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
- •16.Линейные диф.Уравнения высших порядков. Теорема сущ.И единственности. Свойства решений.
- •17.Теорема о структуре общего решения линейного однородного дифференциального уравнения.
- •18. Линейные однородные диф уравнения 2 порядка с постоянным коэффициентом
- •19. Теорема о структуре общего решения линейного неоднородного уравнения
- •20. Нахождение частного решения для линейного диф уравнения 2 порядка с постоянным коэф и спец правой частью
- •24. Знакоположительные ряды. Первый и второй достаточный признаки сходимости рядов
- •25. Знакоположительные ряды. Признак Даламбера и интегральный признак Коши
- •26.Знакочередующиеся ряды.Признак Лейбница.Абсолютно и условно сходящиеся ряды.
- •27.Знакопеременные ряды. Достаточный признак сходимости. Абсолютно и условно сходящиеся ряды.
- •28.Функциональные ряды. Область сходимости ряда, достаточный признак сходимости.
- •29.Степенные ряды. Радиус сходимости степенного ряда
- •31. Ряд Тейлора.
- •32. Разложение основных эл-ных ф-й в ряд Тейлора.
- •33. Применение рядов к приближенным выч.М и решению дифференциальных уравнений.
- •34.Задачи приводящие к понятию двойного интеграла. Двойной интеграл и его выч..
- •35. Тройной интеграл и его выч..
- •36.Криволинейные интегралы первого и второго рода и их выч.
- •37. Основные понятия и определения теории вероятностей. Классическое определение вероятности.
- •38. Сумма событий. Теорема сложения вероятностей.
- •39. Произведение событий. Теорема умножения вероятностей.
- •40. Формула полной вероятности.
- •41. Схема Бернулли. Формула Бернулли.
- •42. Локальная и интегральная теоремы Лапласа. Формула Пуассона.
- •43. Дискретные случайные величины.
- •44. Числовые характеристики дискретных случайных величин.
- •45.Непрерывные случайные величины. Интегральная и дифференциальная ф-и распределения.
- •46.Числовые характеристики непрерывных случайных величин.
- •48. Нормальный з-н распределения.
- •49.Основные понятия математической статистики. Генеральная совокупность и выборка. Вариационный и интервальный статистические ряды. Полигон. Гистограмма. Эмпирическая ф-я распределения.
- •50.Точечные оценки параметров распределения. Их свойства и выч..
- •51. Интервальные оценки параметров распределения. Доверительный интервал для математического ожидания нормального з-на распределения при известном .
- •52.Интервальные оценки параметров распределения. Доверительный интервал для математического ожидания нормального з-на распределения при неизвестном .
- •53. Элементы корреляционного анализа. Двумерная случайная величина. Функциональная и корреляционная зависимость
1. Задачи, приводящие к понятию определенного интеграла. Определение определенного интеграла.
1)Задача
о нах. пройденного пути.
Пусть нам известен з-н изменения скорости
в мат. точке как v(t)
и нам нужно найти путь, пройденный за
время (α, β). Если бы она двигалась с
пост. скоростью, то S=vt.
Весь промежуток времени от α до β разобьем
на отрезки [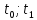 ],[
],[ ]…[
]…[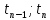 ],
где
],
где
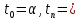 β. Длины эл-ных промежутков обозначены:
β. Длины эл-ных промежутков обозначены:
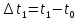

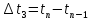 .
На каждом из них обозначим точку:
.
На каждом из них обозначим точку:
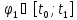 ,
,
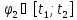 ,
,
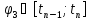 .
Если эл. промежутки достаточно малые,
то скорость на каждом из них можно
считать равной скорости в выбранной
точке.
.
Если эл. промежутки достаточно малые,
то скорость на каждом из них можно
считать равной скорости в выбранной
точке.
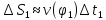 ,
,
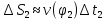 ,
,
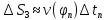 .
Весь пройденный путь:
.
Весь пройденный путь:
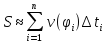 .
За точное значение пути возьмем:
.
За точное значение пути возьмем:
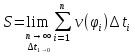
2)Задача
о вычислении площади криволинейной
трапеции.
Для выч. площади криволинейную трапецию
разобьем на n
маленьких эл-ных трапеций. Каждую из
них заменим на прямоугольник и будем
считать, что площадь эл. трапеции ровна
площади соотв. прямоугольника. Для этого
разделим отрезок [a;b]
на n
эл-ных
отрезков [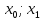 ],[
],[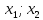 ]…[
]…[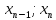 ],
где
],
где
 b.
Длины:
b.
Длины:
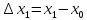

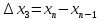 .
На каждом отрезке выберем произв. образом
по точке. Вычислим значение ф-и в этих
точках. Каждую из эл-ных трапеций заменим
прямоугольником с тем же основанием,
но высотой равной значению ф-и в выбранной
точке. Если эл-ные трапеции достаточно
малы, то их площади приблизительно равны
площадям прямоугольников, а суммарная
площадь ровна приблизительно площади
криволинейной трапеции:
.
На каждом отрезке выберем произв. образом
по точке. Вычислим значение ф-и в этих
точках. Каждую из эл-ных трапеций заменим
прямоугольником с тем же основанием,
но высотой равной значению ф-и в выбранной
точке. Если эл-ные трапеции достаточно
малы, то их площади приблизительно равны
площадям прямоугольников, а суммарная
площадь ровна приблизительно площади
криволинейной трапеции:
 .
За точное значение берется предел, когда
число разбиений n
->∞,
а каждый из эл-ных отрезков стягивается
в точку, т. е.
.
За точное значение берется предел, когда
число разбиений n
->∞,
а каждый из эл-ных отрезков стягивается
в точку, т. е.
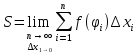 .
.
Определение:1)отрезок
[a;b]
произв. образом разобьем на n
эл-ных
отрезков [ ],[
],[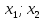 ]…[
]…[ ],
где
],
где
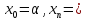 b,
b,
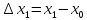


2)на
каждом из эл-ных отрезков выберем
произвольную точку, принадлежащую
определенному отрезку, и вычислим
значение точки


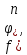
3)составим
сумму произведений:
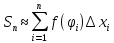 .
.
4)Рассмотрим пример данной интегральной суммы, когда число разбиений n –>∞, а каждый из эл-ных отрезков стягивается в точку.
Если этот предел сущ. и конечен и независим от способа разбиения отрезка, выбора точек, то он наз. определенным интегралом от ф-и y=f(x) на отрезке [a;b].
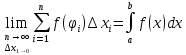
2. Теорема существования определенного интеграла. Свойства определенного интеграла.
Теорема о существовании ОИ
Если
ф-я f(x)
непрерывна на отрезке [a;b]
или имеет на этом отрезке конечное число
точек конечного разрыва, то интеграл
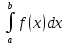 сущ..
сущ..
Свойства ОИ:
1) Постоянный множитель можно выносить за знак определенного интеграла;
2) При изменении направления знак меняется;
3)  ;
;
4)
f(x)≤g(x),
 ;
;
5)
Пусть m
–
наименьшее значение ф-и f(x
), М – наибольшее
значение ф-и f(x
)на
отрезке [a;b],
тогда
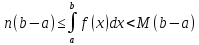 ;
;
6)
Найдется такая точка C,
лежащая на отрезке [a;b],
что

7)
3. Теорема о связи определенного и неопределенного интегралов. Формула Ньютона-Лейбница.
Рассмотрим
определенный интеграл

Если мы будем менять b, то будут изменяться и значения интеграла, т.е. интеграл будет явл. ф-ей вернего предела. Для того, чтобы иметь привычное обозначение, обозначим b через x:
f(x)=

Этот интеграл явл. ф-ей переменной х и наз. интегралом с переменным верхним пределом. Для него справедлива следующая теорема:
Если
f(x) – непрерывная ф-я и φ(x )=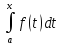 ,то справедливо равенство φ’(x)= f(x).
Другими словами, интеграл с переменным
верхним пределом есть первообразная
для подынтегральной ф-и.
,то справедливо равенство φ’(x)= f(x).
Другими словами, интеграл с переменным
верхним пределом есть первообразная
для подынтегральной ф-и.
Замечание: как мы знаем из определения неопределенного интеграла, НИ есть совокупность всех первообразных, а ОИ с переменным верхним пределом является одной из первообразных.
Формула Н-Л.
Если
F(x ) является какой-либо первообразной
для ф-и f(x) , то интеграл
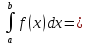 F(b)- F(a)=F(x)
F(b)- F(a)=F(x)
Замечание: заметим, что разность F(b)- F(a) не зависит от выбора первообразной F(x), так как все первообразные отличаются на постоянную величину, которая при вычитании уничтожается.
