Лекция №6

ДЕЙСТВИТЕЛЬНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ

2.1. Функция. Основные понятия, связанные с определением функции

Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.

Пусть даны два непустых множества X и Y. Соответствие f, которое каждому элементу x X сопоставляет один и только один элемент у Y, называется функцией и записывается у = f(x), x X или f : X Y.

Говорят еще, что функция f отображает множество X на множество Y.

Рис. 1.

Например, соответствия f и g, изображенные на рисунке 1 а и б, являются функциями, а на рисунке 1 в и г — нет. В случае в — не каждому элементу xX соответствует элемент уY. В случае г не соблюдается условие однозначности.

Отношение R называется функциональным, если из u следует. Функциональное отношение называется функцией.

Определение 1. Пусть и – произвольные множества действительных чисел. Если на множестве задано отображение , при котором каждому соответствует действительное число , то говорят, что на множестве определена действительная функция действительной переменной . Множество называется областью определения, а множество – множеством значений числовой функции .

Определим арифметические операции над функциями.

Определение 2. Пусть функции и определены на множестве . Суммой называют функцию, значение которой для каждого равно сумме значений функций и для этого значения :

.

Аналогично вводится понятие разности функций:

.

Произведением функций и называют такую функцию на множестве , что

.

Если функция задана на множестве и не обращается на нем в нуль, то через обозначают такую функцию на , что

.

Функцию называют частным функций и и обозначают . Таким образом, .

Понятия суммы, разности, произведения и частного функций применяют и в том случае, когда данные функции имеют различную область определения. В этом случае их рассматривают на пересечении областей определения.

Пример 1. Пусть функция ставит в соответствие каждому числу из отрезка число , а функция ставит в соответствие каждому числу из отрезка число . Найдем сумму этих функций.

Решение. Имеем . Функция ставит в соответствие каждому числу число .

Задать функцию – значит указать закон, по которому каждому значению аргумента из области определения ставится в соответствие значение зависимой переменной из области значений функции.

Наиболее часто используются три способа задания функции: аналитический, табличный и графический. Аналитический состоит в том, что с помощью формулы устанавливается алгоритм вычисления значения функции для каждого из значений аргумента , областью определения функции в этом случае считается множество значений аргумента, при которых данная формула имеет смысл.

Пример 2. Найти область определения функции

.

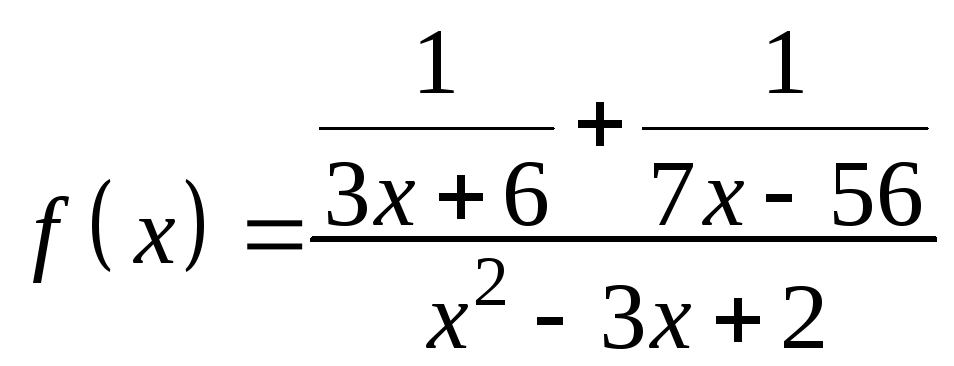Решение. Это выражение имеет числовое значение, если , и . Иными словами, для нахождения области определения надо исключить из корни уравнений , и . Решая эти уравнения, получаем корни: -2, 8, 1, 2 и записываем область определения данной функции

.

В некоторых случаях функция задается на различных числовых множествах разными выражениями, например

или (функция Дирихле)

На практике часто удобным оказывается табличный способ задания функций, например, при экспериментальных измерениях, социологических опросах, при составлении отчетов банковской деятельности и т.д. На табличном способе задания, хранения и обработки информации основаны базы данных. В общем случае таблица имеет вид (табл. 1):

Таблица 1

Она позволяет находить значения функции для выбранных значений аргумента. Таким образом, таблица не задает функции, поскольку для задания функции надо знать ее значения для всех , а не только для некоторых. Существуют методы, позволяющие по такой таблице подбирать выражение , разумеется, с определенной точностью.

При графическом способе соответствие между аргументом и функцией задается посредством графика.

Определение 3. Графиком функции называется множество пар

.

Каждая пара состоит из двух чисел, а потому может быть изображена точкой на координатной плоскости. Следовательно, график числовой функции может быть наглядно изображен множеством точек координатной плоскости.

Обычно графиком функции является некоторая линия. Однако, не всякое множество точек плоскости является графиком некоторой функции. Из определения функции следует, что каждому значению соответствует только одно значение , а потому прямая, параллельная оси ординат, может пересекать график функции не более чем в одной точке. Например, окружность не является графиком какой-либо функции, так как прямые, параллельные оси ординат, могут пересекать ее в двух точках; полуокружность на рис. 2, а является графиком функции , а полуокружность на рис. 2, б – графиком функции .

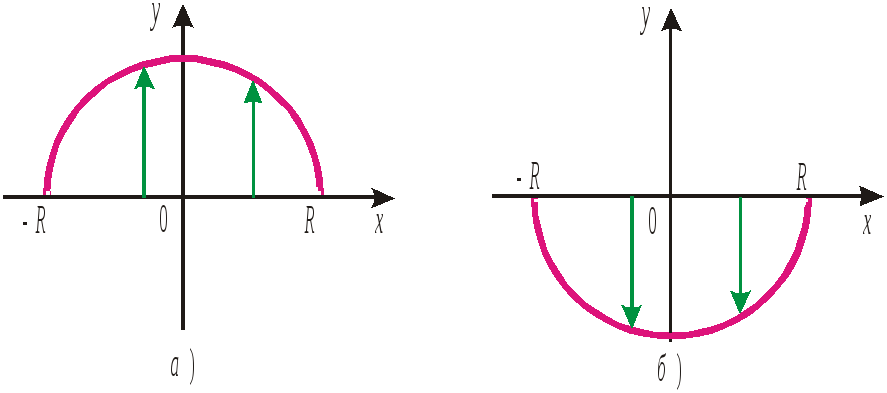
Рис. 2

На практике строят не графики функций, а эскизы таких графиков. Для этого обычно составляют таблицу значений функции для некоторых значений аргумента, наносят на плоскость соответствующие точки и соединяют их линией. При этом предполагается, что график функции является достаточно плавной линией, а найденные точки достаточно точно показывают ход изменения функции. Если эти предположения не выполняются, то построенный график будет сильно отличаться от истинного.

Пример 3. Построим график функции .

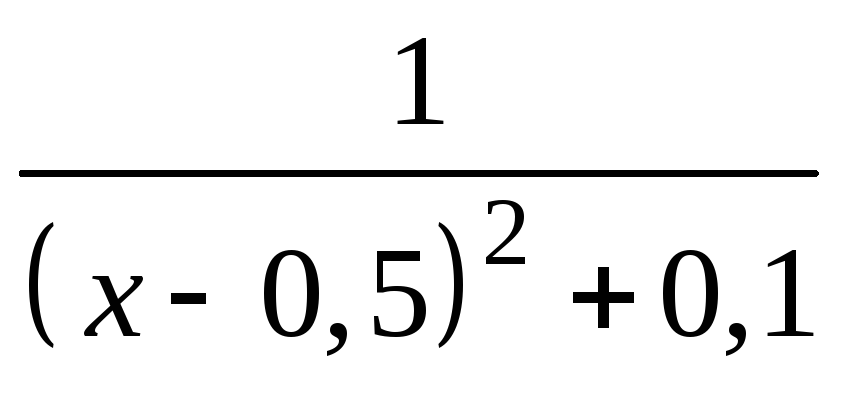Решение. Составляем таблицу значений функции для с шагом 1 (табл.2)

Таблица 2

	-3	-2	-1	0	1	2	3	4
	0,10	0,16	0,42	2,86	2,86	0,42	0,16	0,10

Н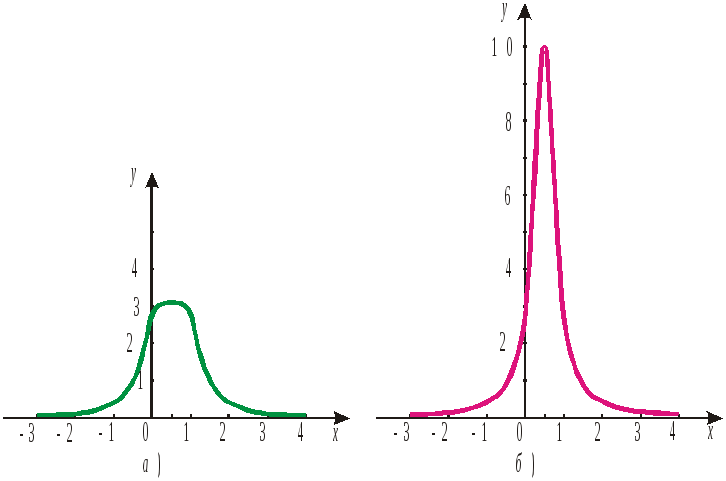 аносим полученные точки на плоскость и соединяем их плавной непрерывной линией. Получаем график, изображенный на рис. 3, а. Заметим, что этот график значительно отличается от истинного (рис. 3, б) в связи с большим значением шага таблицы.

Рис. 3

Не всякий график изображается непрерывной линией, например график функции

имеет один разрыв (рис. 4), а график функции - целая часть числа – имеет бесконечное число разрывов (рис. 5).

Рис. 4 Рис. 5

Встречаются функции, графики которых невозможно изобразить. Примером такой функции является функция Дирихле, определенная выше. Так как на сколь угодно малом отрезке числовой прямой имеются как рациональные, так и иррациональные точки, то график функции Дирихле не является линией. Он состоит из точек оси абсцисс с иррациональными абсциссами и точек прямой с рациональными абсциссами. Построить такой график невозможно.

Пусть известны графики заданных на функций и . Чтобы построить график функции , достаточно для каждого сложить ординаты графиков этих функций. Чтобы построить график функции , достаточно для каждого перемножить ординаты графиков функций и . При этом обращается в нуль, если хотя бы одна из функций , обращается в нуль в данной точке. График функции строят, деля на ординаты графика функции . При этом в точках, где обращается в нуль, функция не определена. Обычно около этих точек график функции неограниченно удаляется от оси абсцисс.

Пример 4. Построим график функции .

Решение. Строим график функции . Прибавляя 1 к ординатам этого графика, получаем график функции . Выполняя деление числа 6 на ординаты последнего графика, получаем ординаты графика функции . Перемножая найденные ординаты и ординаты графика функции , получаем искомый график. На рис. 6 изображено последовательное построение графика функции .

Рис. 6

На практике применяются приборы, автоматически записывающие ход изменения некоторых величин с течением времени (осциллографы, термографы, сейсмографы и т.д.). Они задают графики этих величин как функции времени. Следует иметь в виду, однако, что это задание является лишь приближенным, так как получающаяся линия имеет некоторую толщину, и потому значение , соответствующее данному значению , определяется по графику лишь приближенно.

Определение 4. Пусть числовая функция задана на множестве , а функция – на множестве , и пусть . Тогда существует отображение множества в , задаваемое формулой . Это отображение является числовой функцией, заданной на множестве , и называется суперпозицией (композицией) функций или сложной функцией.

Для математического анализа наиболее существенным является случай, когда функции и заданы своими выражениями и . В этом случае выражение функции получается следующим образом: в выражении каждое вхождение буквы заменяется выражением .

Пример 5. Найдем выражение для суперпозиций и , где , .

Решение. Заменяя в выражении каждое вхождение буквы на , получаем выражение для функции . Таким же образом получаем выражение для функции .

Может случиться, что множество значений выражения, задающего функцию , не является подмножеством области определения функции . Тогда выражение, полученное подстановкой выражения для в выражение для , определяет функцию лишь для тех , при которых .

Пример 6. Найдем область определения функции , если , .

Решение. Так как имеет значение лишь при , то искомая область определения функции задается неравенством . Из него находим, что .