
Глава 2
ПОСЛЕДОВАТЕЛЬНОСТИ
ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
2.1. Определение последовательности, способы задания,
операции над последовательностями
Определение
1. Последовательностью
действительных чисел называется
отображение
![]() ,
определенное на множестве всех натуральных
чисел Кратко ее обозначают символом
,
определенное на множестве всех натуральных
чисел Кратко ее обозначают символом
![]() .
Число
.
Число
![]() называется общим членом
последовательности. Иными словами,
последовательность считается заданной,
если указан способ получения любого ее
элемента.
называется общим членом
последовательности. Иными словами,
последовательность считается заданной,
если указан способ получения любого ее
элемента.
Пример
1.
![]() .
Тогда имеем
.
Тогда имеем
![]() ,
,
![]() и т.д.
и т.д.
Заметим,
что обратная операция – нахождение
выражения
![]() -го
члена последовательности по нескольким
первым членам этой последовательности
– не имеет однозначного решения.
-го
члена последовательности по нескольким
первым членам этой последовательности
– не имеет однозначного решения.
Последовательности
могут быть заданы и соотношением,
задающим выражение
![]() -го
члена последовательности через ее
предыдущие члены.
-го
члена последовательности через ее
предыдущие члены.
Пример
2. Равенства
![]() ;
;
![]() ,
,
![]() ,
,
![]() (
(![]() )
определяют соответственно арифметическую
и геометрическую прогрессии. Рекуррентно
задана и последовательность
Фибоначчи
)
определяют соответственно арифметическую
и геометрическую прогрессии. Рекуррентно
задана и последовательность
Фибоначчи
![]() ,
в которой каждый член (начиная с третьего)
равен сумме двух предыдущих. Полное
рекуррентное задание этой последовательности
таково:
,
в которой каждый член (начиная с третьего)
равен сумме двух предыдущих. Полное
рекуррентное задание этой последовательности
таково:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Определение
2. Последовательности
![]()
![]()
![]() и
и
![]() называются соответственно суммой,
разностью,
произведением
и частным
двух последовательностей
называются соответственно суммой,
разностью,
произведением
и частным
двух последовательностей
![]() и
и
![]() (для частного
(для частного
![]() ).
).
2.2. Предел последовательности. Частичные пределы, верхний и нижний пределы
Рассмотрим
последовательность с общим членом
![]() ,
при
,
при
![]() члены последовательности неограниченно
приближаются к 1. На языке математического
анализа выражение «неограниченно
приближается» означает, что какое бы
малое число
члены последовательности неограниченно
приближаются к 1. На языке математического
анализа выражение «неограниченно
приближается» означает, что какое бы
малое число
![]() мы ни взяли, начиная с некоторого номера
мы ни взяли, начиная с некоторого номера
![]() все члены последовательности будут
сколь угодно мало отличаться от
все члены последовательности будут
сколь угодно мало отличаться от
![]() .
.
Определение
1. Число
![]() называется пределом последовательности
называется пределом последовательности
![]() ,
если для любого положительного числа
,
если для любого положительного числа
![]() существует такой номер
существует такой номер
![]() ,
что при всех
,
что при всех
![]() выполняется неравенство
выполняется неравенство
![]() .
Обозначение
.
Обозначение
![]() .
Кратко определение предела записывается
так:
.
Кратко определение предела записывается
так:
![]() .
.
Неравенство
![]() равносильно двойному неравенству
равносильно двойному неравенству
![]() ,
которое показывает, что элементы
,
которое показывает, что элементы
![]() при
при
![]() находятся в окрестности точки
находятся в окрестности точки
![]() .
Поэтому геометрически определение
предела формулируется так.
.
Поэтому геометрически определение
предела формулируется так.
Определение
2. Число
![]() называется пределом последовательности
называется пределом последовательности
![]() ,
если для любой
,
если для любой
![]() -окрестности
точки
-окрестности
точки
![]() найдется такое натуральное число
найдется такое натуральное число
![]() ,
что все значения
,
что все значения
![]() ,
для которых
,
для которых
![]() ,
попадут в
,
попадут в
![]() -окрестность
точки
-окрестность
точки
![]() .
.
Ясно, что чем
меньше
![]() тем больше число
тем больше число
![]() ,
но в любом случае внутри
,
но в любом случае внутри
![]() -окрестности
точки
-окрестности
точки
![]() находится бесконечное число членов
последовательности, а вне ее находится
лишь конечное число членов последовательности.
находится бесконечное число членов
последовательности, а вне ее находится
лишь конечное число членов последовательности.
Выясним геометрический смысл определения предела последовательности.
Неравенство |xn – a|<ε равносильно неравенствам -ε < xn - а <ε или а - ε < xn < a+ ε, которые показывают, что элемент xn находится в ε -окрестности точки а.
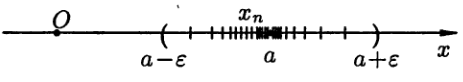
Рис.1
Поэтому определение предела последовательности геометрически
можно сформулировать так: число а называется пределом последовательности {xn}, если для любой ε-окрестности точки а найдется натуральное число N, что все значения xn , для которых n > N, попадут в ε -окрестность точки а (см. рис. 1).
Последовательность, имеющая предел называется сходящейся, а последовательность, не имеющая предела, называется расходящейся.
Например,
последовательность
![]() не имеет предела.
не имеет предела.
Теорема 1. Сходящаяся последовательность имеет только один предел.
Для доказательства утверждения применим метод от противного.
Пусть
![]() и
и
![]() .
Если А1≠А2,
то фиксируем непересекающиеся окрестности
U(A1),
U(A2)
точек А1,
А2.
В качестве таковых
можно взять, например, δ-окрестности
этих точек при δ<
.
Если А1≠А2,
то фиксируем непересекающиеся окрестности
U(A1),
U(A2)
точек А1,
А2.
В качестве таковых
можно взять, например, δ-окрестности
этих точек при δ<![]() │А1–А2│.
По определению предела найдем числа
N1,
N2
такие, что все члены последовательности
│А1–А2│.
По определению предела найдем числа
N1,
N2
такие, что все члены последовательности![]() с номерами n>N1
попадут в окрестность точки А1,
а с номерами n>N2
в окрестность точки А2.
Тогда при n>max{N1,
N2}
получим xn
с номерами n>N1
попадут в окрестность точки А1,
а с номерами n>N2
в окрестность точки А2.
Тогда при n>max{N1,
N2}
получим xn![]() U(A1)
U(A1)![]() U(A2).
Но это невозможно, так как пересечение
U(A1)
U(A2).
Но это невозможно, так как пересечение
U(A1)![]() U(A2)=
U(A2)=![]() .
.
Теорема 2. Если числовая последовательность имеет конечный предел, то она ограничена.
Доказательство:
Пусть![]() .
Полагая в определении предела ε=1,
найдем номер N такой,
что
.
Полагая в определении предела ε=1,
найдем номер N такой,
что
![]() n>N
справедливо неравенство│xn–A│<1.
Значит, при n>N
имеем │xn│<│A│+1.
Если же теперь взять М>max{│x1│,│x2│,…,│xn│,│A│+1},
то получим, что
n>N
справедливо неравенство│xn–A│<1.
Значит, при n>N
имеем │xn│<│A│+1.
Если же теперь взять М>max{│x1│,│x2│,…,│xn│,│A│+1},
то получим, что
![]() n>N
все члены последовательности ограничены
│xn│<М.
n>N
все члены последовательности ограничены
│xn│<М.
Пример
1. Используя определение
предела последовательности, докажем,
что
![]() .
.
Решение.
Зададим произвольное
![]() и рассмотрим модуль разности между
и рассмотрим модуль разности между
![]() -м
членом последовательности и числом 1:
-м
членом последовательности и числом 1:
![]() .
В соответствии с определением предела
последовательности мы должны указать
номер
.
В соответствии с определением предела
последовательности мы должны указать
номер
![]() такой, что
такой, что
![]() выполняется неравенство
выполняется неравенство
![]() .
(1)
.
(1)
Для
отыскания номера
![]() решим неравенство (1) относительно
решим неравенство (1) относительно
![]() .
Получим
.
Получим
![]() .
(2)
.
(2)
Из
неравенства (2) следует, что в качестве
![]() можно взять целую часть числа
можно взять целую часть числа
![]() :
:
![]() .
В самом деле, если
.
В самом деле, если
![]() ,
то
,
то
![]() ,
т.е. справедливо неравенство (2), а значит,
,
т.е. справедливо неравенство (2), а значит,
![]() выполняется неравенство (1).
выполняется неравенство (1).
Итак, для
произвольного
![]() мы указали такой номер
мы указали такой номер
![]() ,
что
,
что![]() выполняется
неравенство
выполняется
неравенство![]() .
Это и означает по определению предела
последовательности, что
.
Это и означает по определению предела
последовательности, что
![]() .
.
Пусть
![]() – некоторая числовая последовательность.
Рассмотрим произвольную возрастающую
последовательность целых положительных
чисел
– некоторая числовая последовательность.
Рассмотрим произвольную возрастающую
последовательность целых положительных
чисел
![]() (
(![]() ).
Выберем из
).
Выберем из
![]() члены с номерами
члены с номерами
![]() :
:
![]() .
.
Полученная
числовая последовательность
![]() называется подпоследовательностью
последовательности
называется подпоследовательностью
последовательности
![]() .
.
Теорема
3. Если
![]() ,
то любая подпоследовательность
,
то любая подпоследовательность
![]() сходится к
сходится к
![]() при
при
![]() .
.
Определение
3. Число
![]() называется предельной
точкой (или частичным
пределом) последовательности
называется предельной
точкой (или частичным
пределом) последовательности
![]() ,
если из последовательности
,
если из последовательности
![]() можно выделить подпоследовательность
можно выделить подпоследовательность
![]() ,
сходящуюся к
,
сходящуюся к
![]() .
.
Можно и по другому сформулировать определение предельной точки.
Определение
4. Число
![]() называется предельной
точкой последовательности
называется предельной
точкой последовательности
![]() ,
если в любой
,
если в любой
![]() -окрестности
точки
-окрестности
точки
![]() содержится бесконечно много членов
последовательности
содержится бесконечно много членов
последовательности
![]() .
.
На языке последовательностей теорема Больцано-Вейерштрасса формулируется так.
Теорема 4 (Больцано-Вейерштрасса). Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Из теоремы 3 следует, что сходящаяся последовательность имеет только одну предельную точку, совпадающую с ее пределом.
Из теоремы 4 следует, что всякая ограниченная последовательность имеет, по крайней мере, одну предельную точку.
Определение
5. Наибольшая (наименьшая)
предельная точка последовательности
![]() ,
ограниченной сверху (снизу), называется
верхним
(нижним)
пределом
этой последовательности и обозначается
,
ограниченной сверху (снизу), называется
верхним
(нижним)
пределом
этой последовательности и обозначается
![]()
![]() .
.
Очевидно,
если
![]() сходится, то
сходится, то
![]()
![]() .
Если последовательность
.
Если последовательность
![]() не ограничена сверху (снизу), то полагают
не ограничена сверху (снизу), то полагают
![]()
![]() .
.
Пример
2. Доказать расходимость
последовательности
![]() .
.
Решение.
Рассмотрим две
подпоследовательности этой
последовательности
![]() и
и
![]() (
(![]() ).
Очевидно, что
).
Очевидно, что
![]() ,
,
![]() .
Таким образом, последовательность
.
Таким образом, последовательность
![]() имеет две предельные точки:
имеет две предельные точки:
![]() и
и
![]() ,
а поэтому не может быть сходящейся,
поскольку сходящаяся последовательность
имеет только одну предельную точку.
,
а поэтому не может быть сходящейся,
поскольку сходящаяся последовательность
имеет только одну предельную точку.
Пример
3. Найти все предельные
точки последовательности
![]() ,
верхний и нижний пределы этой
последовательности.
,
верхний и нижний пределы этой
последовательности.
Решение.
Каждое из чисел
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() встречается в последовательности
бесконечно много раз, поскольку
встречается в последовательности
бесконечно много раз, поскольку
![]()
![]() .
Поэтому каждое указанное число является
предельной точкой последовательности
.
Поэтому каждое указанное число является
предельной точкой последовательности
![]() .
Других предельных точек последовательность
не имеет, так как если число
.
Других предельных точек последовательность
не имеет, так как если число
![]() не совпадает ни с одним из этих 181 чисел,
то существует окрестность точки
не совпадает ни с одним из этих 181 чисел,
то существует окрестность точки
![]() ,
не содержащая ни одного члена
последовательности. Из найденных 181
предельных точек наименьшей является
,
не содержащая ни одного члена
последовательности. Из найденных 181
предельных точек наименьшей является
![]() ,
а наибольшей 1, т.е.
,
а наибольшей 1, т.е.
![]() ,
,
![]() .
.
