
- •Лекция №1
- •1. Понятие производной функции
- •Геометрическая и механическая интерпретации производной
- •2. Правила дифференцирования
- •Производные основных элементарных функций
- •Дифференцирование сложной функции
- •3. Понятие дифференциала функции
- •4. Приближенные вычисления с помощью дифференциала
- •5. Частные производные и полный дифференциал
- •6. Понятие неопределенного интеграла, свойства.
- •7. Методы интегрирования
- •8. Понятие определенного интеграла, свойства
- •9. Дифференциальные уравнения
Лекция №1
Тема: Основы математического анализа
План:
-
Понятие производной функции
-
Правила дифференцирования функции
-
Понятие дифференциала функции
-
Приближенные вычисления с помощью дифференциала
-
Частные производные и полный дифференциал
-
Понятие неопределенного интеграла, свойства
-
Методы интегрирования
-
Понятие определенного интеграла, свойства
-
Дифференциальные уравнения
1. Понятие производной функции
Рассмотрим
функцию
![]() ,
определенную в интервале [a,
b].
,
определенную в интервале [a,
b].
Пусть xo
и x
– два произвольных значения из этого
интервала. Обозначим x
– xo
= Δx,
откуда x
= хo
+
Δx.
Говорят, что
для перехода от значения аргумента хo
к значению x
первоначальному
значению придано приращение Δx.
Приращением
Δy
функции
![]() ,
соответствующим приращению Δx
аргумента
x
в точке xo
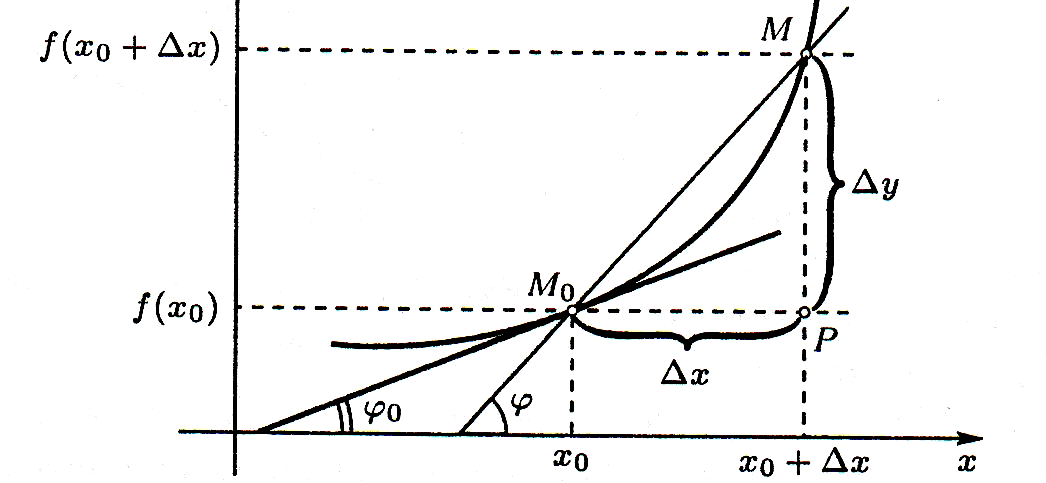
(рис. 1),
называется разность
,
соответствующим приращению Δx
аргумента
x
в точке xo
(рис. 1),
называется разность
Δy = f(xo + Δx) – f(хo). (1)
![]()
Рис. 1
Пусть
![]() определена на некотором промежутке и
пусть xo
– некоторая
точка этого промежутка. Пусть Δx
– приращение к значению аргумента
такое, что (xo
+ Δx)
не выходит
за пределы упомянутого промежутка, а
Δy
= f(xo
+ Δx)
– f(хo)
– соответствующее приращение функции.
определена на некотором промежутке и
пусть xo
– некоторая
точка этого промежутка. Пусть Δx
– приращение к значению аргумента
такое, что (xo
+ Δx)
не выходит
за пределы упомянутого промежутка, а
Δy
= f(xo
+ Δx)
– f(хo)
– соответствующее приращение функции.
Определение.
Если существует ![]() , то этот предел называется производной
от функции
, то этот предел называется производной
от функции
![]() по переменной x
в точке xo
(обозначения:
по переменной x
в точке xo
(обозначения:
![]() или у'х).
Итак:
или у'х).
Итак:
у'х
=
![]() =
= ![]() (2)
(2)
Если предел (2) конечен, то производная называется конечной, если же этот предел бесконечен, то у'х — бесконечная производная.
Если конечная производная существует в каждой точке некоторого множества, то она оказывается функцией от x , заданной на этом множестве.
Геометрическая и механическая интерпретации производной
-
Если x = f(t) есть уравнение прямолинейного движения точки,
то производная представляет собой скорость точки в момент времени t.
Быстрота протекания физических, химических, биологических и других процессов, например скорость охлаждения тела, скорость химической реакции и т.п., также выражается при помощи производной.
Пример.
Предположим, что температура тела Т
есть убывающая
функция времени: Т = f(t).
Пусть t
— фиксированный
момент времени. Если t
получает
приращение Δt,
температура
T
уменьшается
на ΔT;
тогда отношение
ΔT
/ Δt
представляет
среднюю скорость охлаждения тела. Предел
этого отношения при Δt
![]()
![]() ,
т.е.
,
т.е. ![]() = f
'(t)
выражает
скорость охлаждения тела в данный момент
t.
= f
'(t)
выражает
скорость охлаждения тела в данный момент
t.
Таким образом, скорость охлаждения тела равна производной температуры тела по времени.
2. Производная
f'(х)
функции
![]() геометрически
представляет собой угловой коэффициент
касательной к графику этой функции в
точке с абсциссой x.
геометрически
представляет собой угловой коэффициент
касательной к графику этой функции в
точке с абсциссой x.
При этом если существует касательная, то существует и производная, и наоборот. Случаю касательной, не параллельной оси
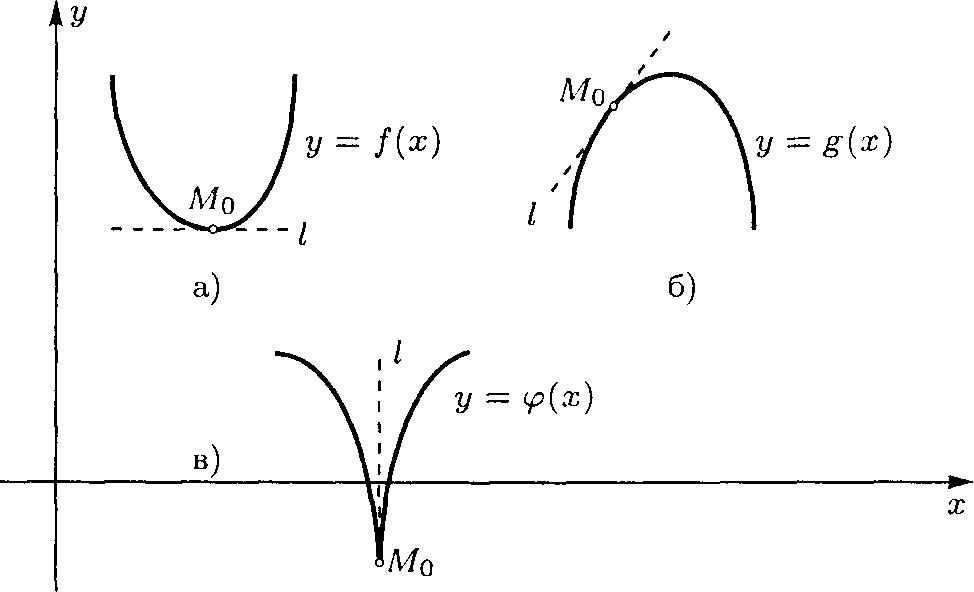
Рис. 2 (а и б – конечные производные в точке М0; в – бесконечная производная в точке М0)
ОУ, отвечает конечная производная, параллельной оси ОУ — бесконечная производная (рис. 2).
2. Правила дифференцирования
1. Производная от постоянной величины равна нулю, т. е. если у = C, то y' = 0:
C' = 0. (3)
2. Производная алгебраической суммы конечного числа функций равна сумме производных слагаемых:
(u + v + w + . . .)' = u' + v' + w' + . . . (3)
3. Производная произведения двух функций определяется формулой:
(u ∙ v )' = u' ∙ v + u ∙ v' (4)
4. Производная частного от деления двух функций опреде ляется формулой:
![]() (5)
(5)
Пример 1.
Найти производную функции
![]() .
.
Используя таблицу производных, получаем:
![]() ,
,
![]()
Пример 2. Найти производную функции y = x ∙ sinx.
Используя правило дифференцирования произведения, получим:
![]() .
.
