Частный институт управления и предпринимательства
Е. М. Светлая основы высшей математики и информатики Элементы теории множеств и математической логики
Учебно-методическое пособие
Минск 2008
УДК 51+004
ББК 22.1(67)я73; 32.973.2я7
С 24
Рекомендовано к изданию редакционно-издательским советом Частного института управления и предпринимательства
А в т о р
старший преподаватель кафедры высшей математики и статистики Частного института управления и предпринимательства Е. М. Светлая
Р е ц е н з е н т
доцент кафедры высшей математики Белорусского государственного экономического университета кандидат физико-математических наук, доцент А. И. Астровский
Рассмотрено и одобрено на заседании кафедры высшей математики и статистики, протокол № 7 от 28.02.2008 г.
Светлая, Е. М.
С 24 Основы высшей математики и информатики. Элементы теории множеств и математической логики: учеб.-метод. пособие / Е. М. Светлая.– Минск: Частн. ин-т упр. и предпр., 2008.– 16 с.
Пособие подготовлено в соответствии с учебной программой ЧИУиП по дисциплине «Основы высшей математики и информатики» для студентов специальности «Правоведение».
Содержит основные понятия теории множеств, математической логики и сопровождается пояснениями с примерами, иллюстрациями, упражнениями.
Предназначено также для студентов экономических специальностей дневной и заочной форм обучения Частного института управления и предпринимательства.
УДК 51+004
ББК 22.1(67)я73; 32.973.2я7
© Светлая Е. М., 2008
©
Частный институт управления и
предпринимательства, 2008
Лекция 1. МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ
План:
1. Основные понятия.
2. Операции над множествами.
3. Алгебраические свойства операций над множествами.
Ключевые понятия
Множество. Способы задания множеств. Операции объединения, пересечения, дополнения. Разность множеств.
1. Основные понятия
Понятие множества относится к числу первичных математических понятий, т.е. это понятие не имеет логического определения через более простые понятия.
Под множеством понимают совокупность некоторых объектов, объединенных по определенному признаку. Так, можно говорить о множестве студентов института, о множестве книг в библиотеке, о множестве всех натуральных чисел.
Объекты, из которых состоит множество, называются его элементами.
Множество обозначают прописными буквами, а их элементы – строчными буквами.
Принадлежность
элемента а
множеству М
обозначается а
М,
непринадлежность а
М
или а
М.
М
Рис. 1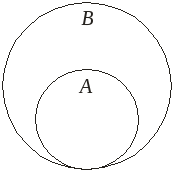
Запись А В означает, что А является подмножеством множества В, не совпадающим с В. В этом случае множество А называется собственным подмножеством множества В.
Множества А и В равны (А = В), если А В и В А.
Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным (например, множества натуральных, целых, вещественных чисел – бесконечные множества).
Мощность множества – число элементов в конечном множестве. Обозначение А.
Понятие мощности множества вводится также и для бесконечных множеств. Однако здесь это обобщение мы рассматривать не будем.
Множество, не содержащие ни одного элемента, называется пустым множеством, обозначается символом . Полагают, что мощность пустого множества равна нулю, т. е. = 0. Кроме того, полагают, что пустое множество является собственным подмножеством любого множества.
Примером пустого множества является множество действительных решений уравнения х2 + 1 = 0.
Множество определяется либо путем записи его элементов в фигурных скобках (т. е. в фигурных скобках перечислены все элементы множества), либо указанием общего свойства, которым обладают все элементы данного множества.
Например, запись А = а, b, c, d означает, что множество А состоит из четырех элементов а, b, c и d; запись А = 1, 2, 4, 8, 16, … означает, что множество А состоит из всех целых чисел, являющихся целыми степенями двойки; запись А = 2, 4, 6, …, 100 означает, что множество А состоит из четных чисел, не превышающих 100; запись А = х: х R и 0 х 4 означает, что множество А состоит из всех действительных чисел, удовлетворяющих неравенству 0 х 4.
Определение множества В = 1, 2, 3, 3, 7 является некорректным, так как при перечислении элементов не следует указывать один и тот же элемент несколько раз.
Пример. Принадлежит ли элемент а множеству В, если известно, что А = а, b, c, d, В = А, С?
Решение. а В, так как элемент а не перечислен в списке элементов множества В.
С понятием «множество» следует обращаться достаточно осторожно, так как свободное обращение с ним может привести к противоречиям (парадоксам). Например, предположение о существовании множества всех множеств приводит к противоречиям.
Другой пример (парадокс брадобрея): в некотором городе брадобрей бреет всех, кто сам не бреется, и не бреет тех, кто сам бреется. К какому множеству отнести брадобрея: кто бреется сам либо бреется у брадобрея?
Для избежания подобных противоречий будем предполагать существование в каждом конкретном случае так называемого универсального множества (универсума) V, такого, что рассматриваемые системы множеств являются его подмножествами.
Например, для множеств целых Z, рациональных Q, натуральных чисел N в качестве универсума можно принять множество действительных чисел R:
N Z Q R.