Выпуклой линейной комбинацией двух точек и называют точку , где . Геометрически это отрезок, соединяющий точки и , которые получатся соответственно при значениях и . Остальные точки отрезка получатся при промежуточных значениях . В частности, середине отрезка соответствует значение .

В общем случае для точек выпуклой линейной комбинацией называется точка

, где , и .

Если такие точки являются вершинами выпуклого многоугольника на плоскости, то любую его точку, как внутреннюю, так и граничную, можно представить в виде их выпуклой линейной комбинации.

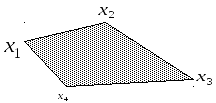
Рис. 2.10

При этом для всех точек границы кроме вершин потребуется использовать точно по две различные точки. Для любой внутренней точки достаточно трех. Вершины в виде выпуклой линейной комбинации различных точек представить нельзя и, согласно определению, они являются угловыми точками.

Можно доказать и в общем случае, что множество допустимых решений задачи линейного программирования, если оно не пусто, является выпуклым. Действительно, в n-мерном пространстве каждое неравенство вида исключает из числа допустимых решений некоторое полупространство. При любом числе таких ограничений область допустимых решений останется выпуклой. Представим себе для наглядности обработку алмаза на плоскошлифовальном станке. Полученный бриллиант всегда будет иметь форму выпуклого многогранника.

Без ограничения общности изложения в дальнейшем будем предполагать, что область допустимых решений является ограниченной. Всегда можно предполагать, что сумма всех переменных реальной задачи не превышает некоторое достаточно большое положительное число.

Докажем теперь сформулированную выше теорему, рассуждая от противного. Пусть – все угловые точки многогранника допустимых решений, а экстремум целевой функции достигается в некоторой внутренней точке многогранника , например, . Но любую внутреннюю точку выпуклого многогранника можно представить как выпуклую линейную комбинацию угловых точек, т. е.

, где , и .

Следовательно, .

Обозначим, тогда

И получается, что .

Поскольку M – значение функционала в одной из угловых точек, то утверждение теоремы, что экстремум достигается в одной из угловых точек многогранника допустимых планов доказано. Остается доказать, что если целевая функция достигает экстремального значения более чем в одной угловой точке, то она принимает это же значение в любой точке, являющейся их выпуклой линейной комбинацией.

Пусть в угловых точках целевая функция принимает свое максимальное значение равное M. Любая точка , являющаяся их выпуклой линейной комбинацией, может быть представлена как

, где , и .

Подставляя в целевую функцию, получим:

.

Значит , что и требовалось доказать.

2.8. Общая идея симплексного метода

Основная теорема линейного программирования может навести на мысль, что можно найти все угловые точки многогранника допустимых планов и сравнить в них значения целевой функции. Пусть задача записана в канонической форме и содержит m равенств с n переменными (m < n),

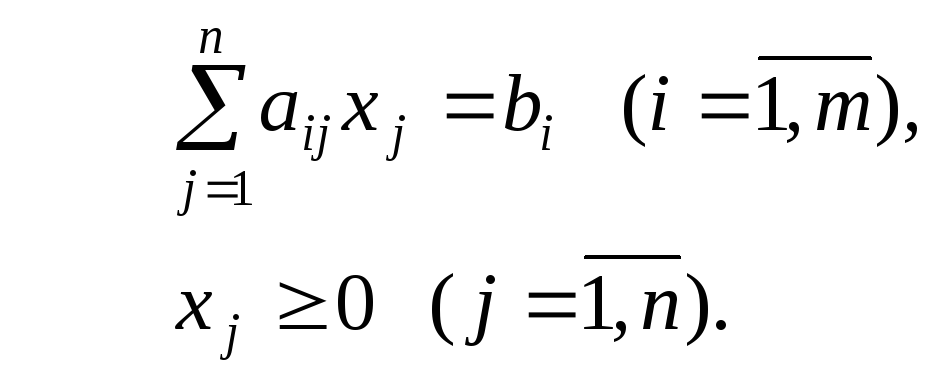
Без ограничения общности можно предполагать, что все уравнения линейно независимы, иначе некоторые можно было бы опустить, и что ранг матрицы коэффициентов системы равен m, в противном случае система несовместна. Произвольно выбирая переменных из их общего числа , положим оставшиеся переменных равными нулю. Общее количество полученных таким путем миноров и соответственно групп уравнений – это число сочетаний из элементов по , которое равно

.

Среди решений этих групп уравнений содержатся все угловые точки множества допустимых планов, но количество таких групп даже для относительно простых задач настолько велико, что поиск оптимального решения простым перебором вершин не имеет смысла. Даже для рассмотренного примера графического решения задачи . (Кроме четырех ограничений надо учитывать и две координатные оси, поэтому ). Попарные пересечения этих прямых дадут все вершины многоугольника области допустимых решений, в том числе и точки экстремума. Часть полученных точек окажется вне области допустимых решений. Видно, что затраты труда при таком подходе сильно увеличиваются. В реальных задачах число переменных измеряется сотнями и тысячами, поэтому разработаны методы рационального перебора угловых точек. К наиболее простым из них относится симплексный метод, в основу которого положена идея последовательного улучшения плана. Если в сложной ситуации не удается определить наилучший путь к цели, то логично сделать шаг, приближающий к этой цели. Чтобы реализовать эту идею сначала введем необходимые термины.

Базисное решение (план). Так называют решение одной из выделенных групп уравнений, если для этой группы оно является единственным. Соответствующие переменных называют базисными, а переменных, которым были присвоены нулевые значения, небазисными, или свободными.

Опорное базисное решение (опорный план). Так называют базисное решение, если все базисных переменных неотрицательны.

Недопустимое базисное решение. Имеет место если хоть одна базисная переменная отрицательна.

Вырожденное базисное решение. Имеет место тогда, когда хоть одна базисная переменная нулевая.

Поскольку ранг матрицы коэффициентов и вектор правых частей ненулевой, то среди ее миноров m-го порядка обязательно будут ненулевые. Значит, базисные решения всегда существуют. Множество базисных решений содержит в своем составе, как подмножество, все угловые точки области допустимых планов.

Алгоритм симплекс-метода нахождения оптимального плана всегда начинается с некоторого допустимого базисного решения. Далее следует проверка, можно ли улучшить значение целевой функции, если увеличить одну из небазисных (нулевых) переменных, ввести ее в базис. Если такой переменной нет, то оптимальное решение найдено. Если есть, то необходимо перейти к новому, лучшему (или хотя бы не худшему) базисному решению. Но базисное решение содержит точно m переменных, поэтому после определения переменной, вводимой в базис, необходимо определить исключаемую из базиса переменную.

Каждый такой цикл преобразования называют итерациями, а методы вычислений, основанные на последовательных итерациях,– итерационными методами.

Многократное повторение однотипных вычислений весьма трудоемко и утомительно, если выполнять его вручную, но если его запрограммировать, то при современной вычислительной технике размерность решаемых задач обычно определяется содержательными проблемами их экономической постановки, а не техническими трудностями расчета.