також може бути замінена протилежною силою (аксіома 4). Розглянемо рів­новагу кожного тіла окремо.

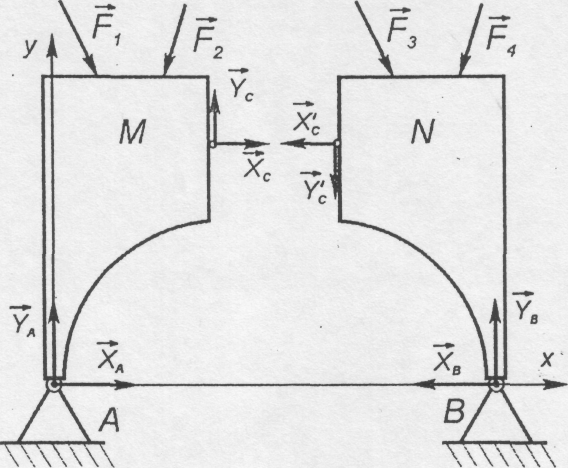
Рис. 4.14

На рис. 4.14 вказані сили, прикладені до тіл М і N, причому силиіявляють собою складові сили, що замінюють дію тіла N на М, а і - складові сили, замінюючи дію тіла М на тіло N. Для кожного тіла ми можемо скласти по три рівняння рівноваги, тобто всього шість рівнянь. Невідомих буде також шість, оскільки згідно аксіоми 4

Такий шлях розв'язання задачі не єдиний. Можна скласти три рівняння рівноваги для тіла М і три для системи тіл М і N, приймаючи їх за одне тверде тіло, або скласти рівняння для тіла N і системи тіл М і N. Якщо тіл буде не два,а більше, наприклад п, то очевидно рівнянь рівноваги в цьому випадку буде Зп.

Питання для самоконтролю

І. Як формулюється лема про паралельний перенос сили? Чому дорівнює момент приєднаної пари?

2. Що називається головним вектором системи сил? Яка різниця між поняттями головного вектора і рівнодійної?

З. Що називається головним моментом системи сил відносно заданої точки?

4. Чому дорівнюють проекції головного вектора і головного моменту на осі декартової системи координат?

5. Як формулюється основна теорема статики?

6. Чи зміниться головний вектор заданої системи сил при зміні точ­ки (центра) зведення ?

7. Як виражається головний момент відносно нового центру зведен­ня, через головний момент відносно початкової точки зведення?

8. Чи завжди просторову систему довільно розміщених сил можна привести до двох мимобіжних сил?

9. Що таке статичні інваріанти?

10. В чому полягає необхідна і достатня умова рівноваги просторової системи довільно розміщених сил?

11. Скільки незалежних рівнянь рівноваги і які можна записати:

- просторової системи, довільно розміщених сил?

- просторової системи паралельних сил?

- плоскої системи довільно розміщених сил?

- системи паралельних сил на площині?

12. Напишіть три форми рівнянь рівноваги для плоскої системи дові­льно розміщених сил.

13. Які задачі називаються статично визначеними і статично невизначеними?

Задача 4.1.

Однорідна балка довжиною АС=2 м і вагою Р=400 Н кінцем А закріплена шарнірно, а проміжною точкою В опирається на нерухому опору. До кінця балки С прикріплений трос, перекинутий через блок D, що несе на другому кінці вантаж ва­гою Q=300 H. Визначити реакції опор в точках А і В, якщо

Рис. 4.15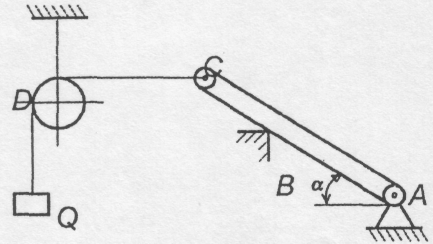

Розв'язання

1. Розглядаємо рівновагу балки АВ (рис. 4.16).

2. Показуємо силу - вагу балки (прикладена до середини балки, оскільки балка однорідна і постійного перерізу). Це-активна сила, що діє на балку.

3. Звільняємо балку від в'язей прикладених на неї. В'язями є нерухомий циліндричний шарнір А, трос, перекинутий через блок D (в блоці тертям знехтувати), і опора В. Реакція опори В направлена перпендикулярно до балки АС. Реакція шарніра А невідома, ні за величиною, ні за напрямком, тому будемо шукати цю реакцію у вигляді двох проекцій і ; оскільки блок D рахується ідеальним, то натяг троса буде рівним вазі Q.

4.Вибираємо систему координат, як вказано на рисунку (4.16).

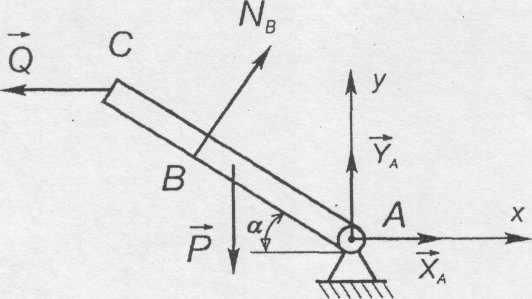
Рис. 4.16

На балку діє плоска система довільно розміщених сил

5.Складаємо рівняння рівноваги:

1). ;

2). ;

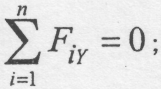3).

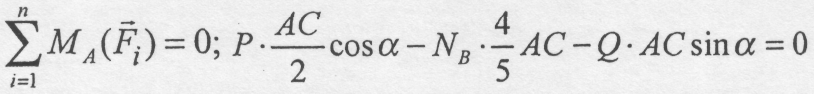
Розв'язуючи одержані рівняння знаходимо:

З третього рівняння

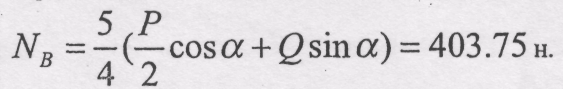
З першого рівняння

З другого рівняння

Задача 4.2

До балки АВ, зображеної на рис. 4.17, прикладена сила F = 1600н. і рі­вномірно розподілене навантаження інтенсивності q=120 н/м. Кут α = 30°, а =3м., b =7м, l=12м. Вага балки Р=500н. Визначити реакції опор.

Розв'язання.

Розподілене навантаження замінюємо її рівнодійною . Сила , буде прикладена на середині відрізка СВ. Дії опор замінюємо в точці А реакціями X_A , Y_A і в точці В реакцією . перпендикулярної до опорної поверхні котків.

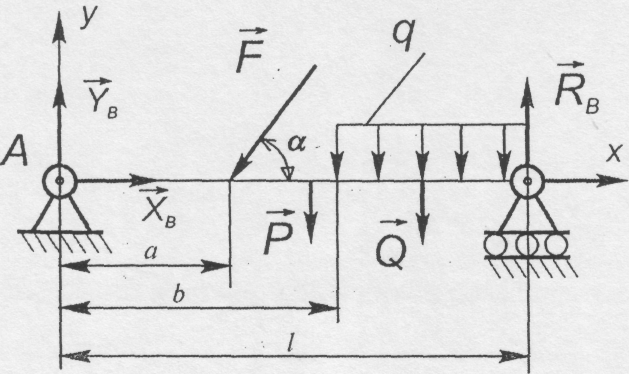
Рис. 4.17

На балку діє плоска система довільно розміщених сил.

Складаємо рівняння рівноваги:

1).

2).

3).

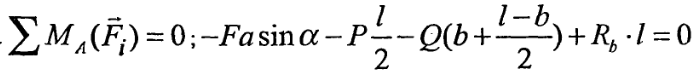
Розв'язуючи ці рівняння одержимо:

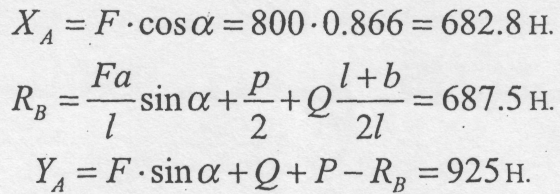
Задача 4.3

На балку, вага якої Q і довжина l, прикладена в точці В сила (рис. 4.18). Визначити реакції в точці А. На закріплений кінець балки діє роз­поділене навантаження, яке в точці А можна привести до однієї сили реакції , яка невідома за величиною і напрямком і до пари сил з невідомим моментом М_А . Розкладаючи силу R_A на дві складові і . можна записати наступні рівняння рівноваги (на балку діє плоска система довільно розміщених сил)

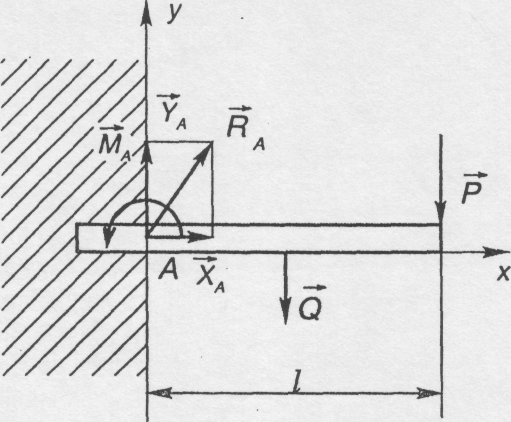
Рис. 4.18

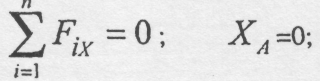
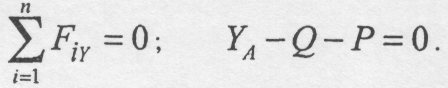
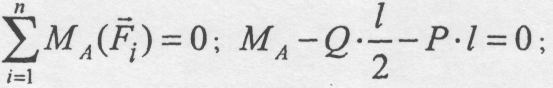
Звідки

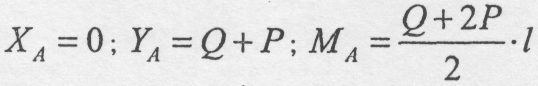
Задача 4.4

Два однорідні бруски однакової довжини з'єднані шарнірне в точці С, а в точках А і В шарнірно прикріплені до опор. Вага, кожного бруска дорів­нює Р. В точці С підвішений вантаж Q. Відстань AB=d. Відстань від точки С до горизонтальної прямої АВ рівна Ь. Визначити реакції шарнірів А і В. (рис.4.19).

Розв'язок

Замінюючи дію опор реакціями, спочатку розглянемо рівновагу сис­теми брусів в цілому (рис. 4.20,а).

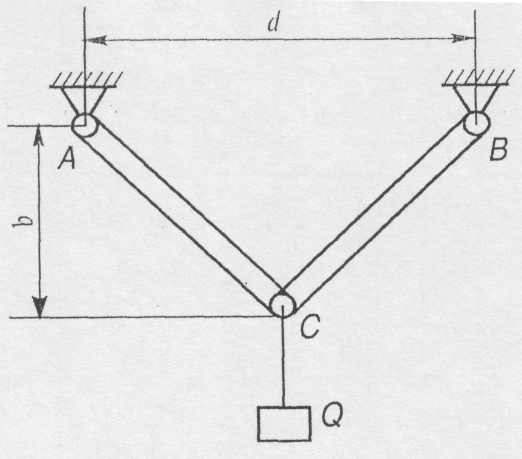
Рис. 4.19

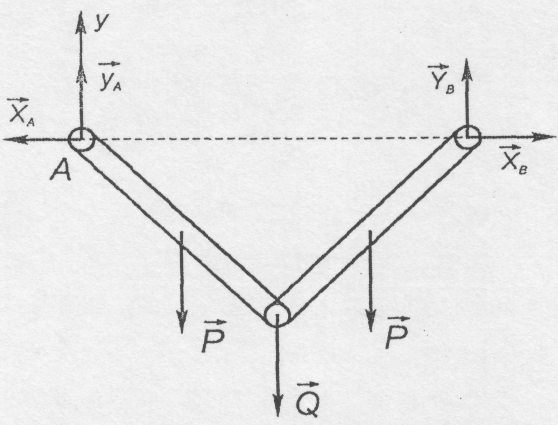
Рис. 4.20,а

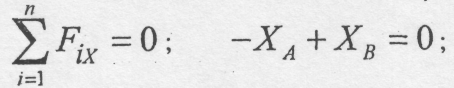
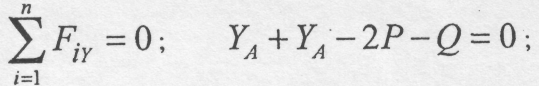
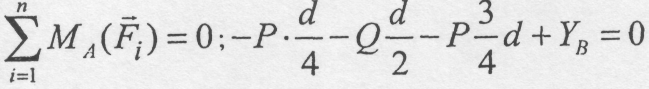
З цих рівнянь знаходимо

Для знаходження X_A розглянемо рівновагу лівого бруса (рис. 4.20, б) і складемо рівняння.

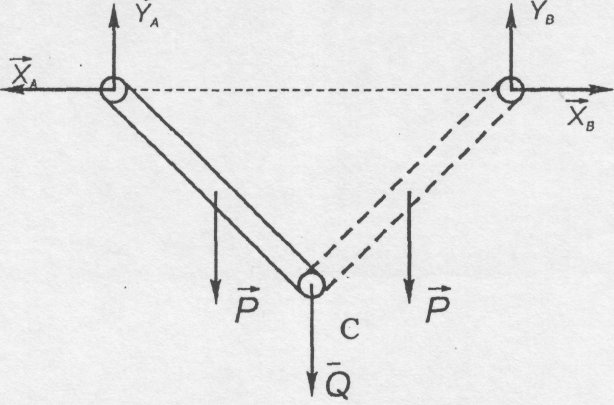
Рис. 4.20,6

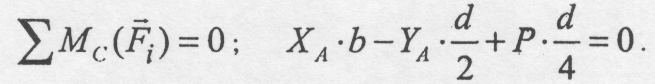
Звідки

В цій задачі не вимагалось знайти внутрішню силу в шарнірі С; тому, ми і не складали двох других рівнянь рівноваги і не показали цю силу на рис. 4.20,6.

Задача 4.5

Однорідна прямокутна кришка (рис.4.21) вагою 400Н. Нахилена під кутом α = 60° до вертикальної площини й утримується в такому положенні з допомогою сферичного шарніра О, циліндричного шарніра А і троса CD, який знаходиться в горизонтальній площині. Знайти реакції шарнірів і троса, якщо ОА=ВС= а , ОС=АВ=0,6 а .

Розв'язання

1. Розглядуємо рівновагу кришки ОАВС (рис.4.22)

2. Показуємо активну силу - вагу кришки.

3. Звільняємо кришку від в'язей, замінюючи дію в'язей реакціями. В'язями є сферичний шарнір О, циліндричний шарнір А і трос CD. Реакцію сферичного шарніра О розкладаємо на три складові: . Реакцію циліндричного шарніра А розкладаємо на дві складові:

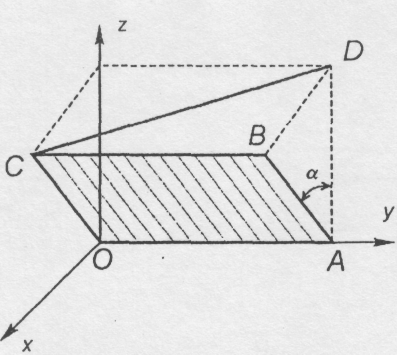
Рис. 4.21

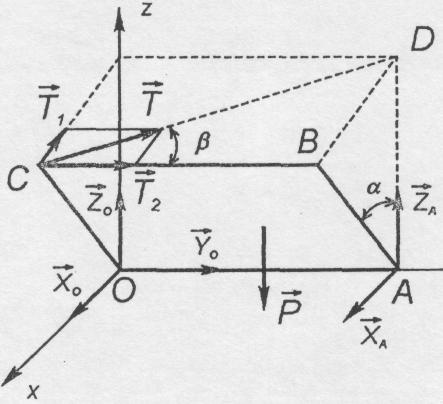
Рис. 4.22

4. Вибираємо систему координат, як показано на рисунках.

5. Складаємо рівняння рівноваги просторової системи довільно роз­міщених сил, що діють на кришку:

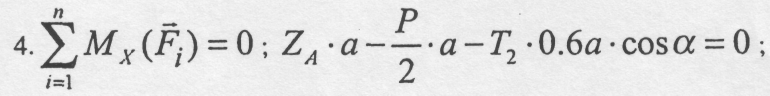
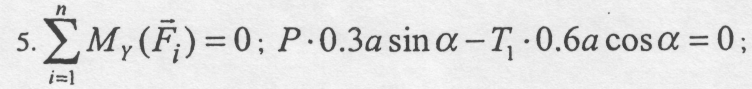
де

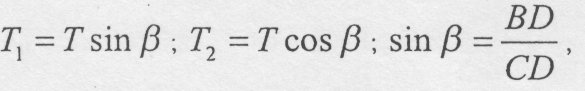
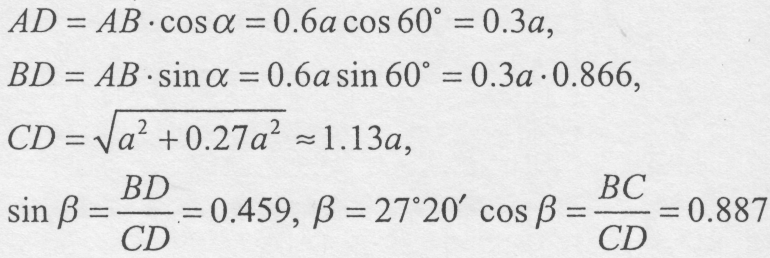
З п'ятого рівняння визначається T₁, а потім і

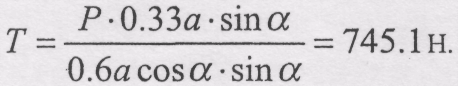
З другого рівняння

З шостого рівняння

З четвертого рівняння

З третього рівняння Z₀ = О ;

З першого рівняння Х₀ = 0 ;

Знак мінус для Y₀ говорить про те, що напрямок, складової реакції Y₀ на рис. 4.20 вказано неправильно. Складова Y₀ дійсно направлена в про­тилежний бік до осі у .

Задача 4.6.

Знайти зусилля в шести опорних стрижнях, що підтримують квадра­тну плиту ABCD. при дії горизонтальної сили вздовж сторони AD. Розміри вказані на рис. 4.23. Вагою плити і стрижнів нехтувати. Опорні стрижні при­кріплені до плити і нерухомих пристроїв сферичними шарнірами.

Внаслідок шарнірного закріплення опорних стрижнів їх реакції на плиту направлені вздовж стрижнів. Позначимо ці реакції у відповідності з номерами стержнів, тобто . Вибираємо систему координат як вказано на рис. 4.23.

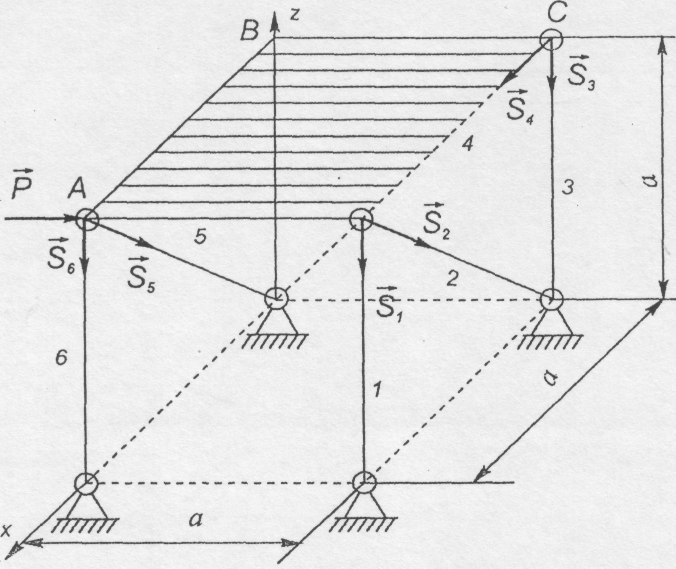
Рис. 4.23

Послідовність розв'язку, аналогічна розв'язку задачі 4.5.

1.

2.

3.

4.

5.

6.

Розв'язуючи ці рівняння, одержимо:

Глава 5*. Ферми

5.1. Основні поняття про статично визначені плоскі ферми

Фермами називають геометрична незмінні системи прямоліній­них стрижнів, з'єднаних між собою шарнірами.

Найпростішим прикладом ферми є система трьох стрижнів, з'єднаних між собою шарнірами. З усього класу геометричне незмін­них ферм без зайвих стрижнів виділимо прості ферми, їх побудова відбувається так: розглядається основний трикутник, до нього двома стержнями приєднується новий шарнір (вузол) і т.д.

Встановимо залежність між кількістю (п) стрижнів і кількістю (k) шарнірів (вузлів) в простих фермах.

В основному трикутнику, маємо три стрижні і три вузли. Для незмінного з'єднання з основою ферми решти К-3 шарнірів (вузлів) необхідно два стрижні. Отже, загальна кількість стрижнів у найпрос­тішій фермі разом з трьома стрижнями основного трикутника визнача­ється так:

(5.1)

Для статичної означеності задачі достатньо виконання умови (5.1).

За своїм призначенням ферми, частіше всього, діляться на мос­тові, крокв'яні і кранові (рис. 5.1 а,б,в).

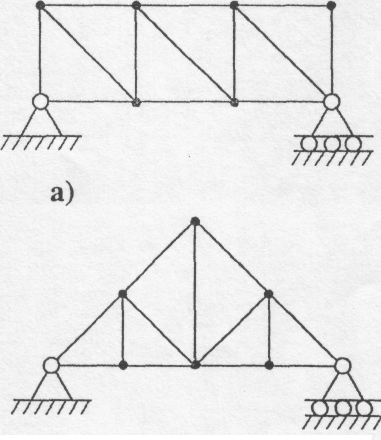
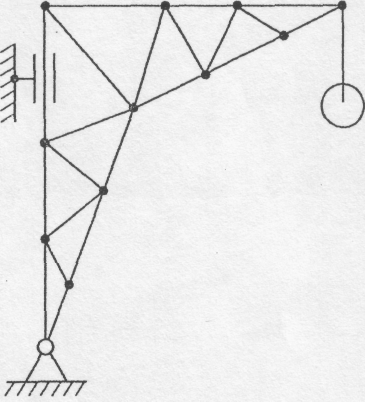
б) в)

Рис. 5.1

Термінологія:

1. Вертикальні стрижні-стояки.

2. Стрижні зовнішнього контуру ферми, відповідно верхній і нижній пояс.

3. Стрижні, нахилені під різними кутами до горизонту - роз­коси.

Основна задача розрахунку простих ферм полягає у визначен­ні внутрішніх сил, що виникають в стрижнях ферми внаслідок дії ак­тивних зовнішніх навантажень.

Цю задачу розв'язують, опираючись на деякі спрощення в її постановці:

1. Вважають шарніри ідеальними точковими шарнірами без тертя.

2. Усі стрижні вважають абсолютно твердими.

3. Зовнішні сили, прикладені до ферми, вважають прикладе­ними у вузлах.

При цих припущеннях можна вважати, що кожен стрижень фер­ми розтягнутий або стиснутий. Зусилля в окремих стрижнях наванта­женої ферми можуть бути рівними нулю. Такі стрижні прийнято нази­вати "нульовими". Розглянемо леми, користуючись якими, можна ви­значити нульові стрижні плоскої ферми, не проводячи її розрахунку.

Лема 1. Якщо в не навантаженому вузлі простої ферми схо­дяться два стрижні, то зусилля в цих стрижнях дорівнюють нулю (рис. 5.2,а).

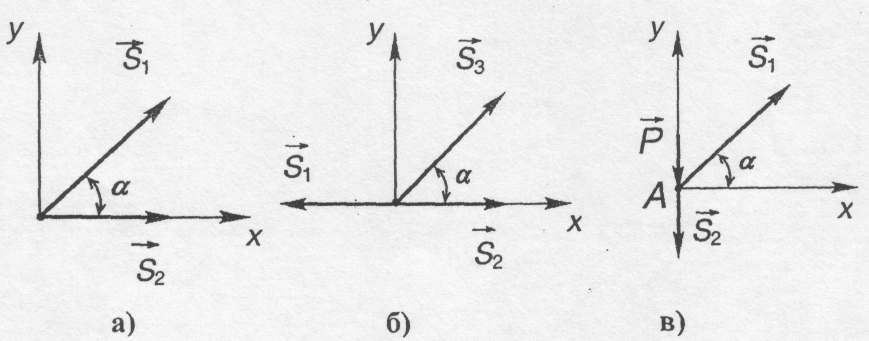
Рис. 5.2

Складемо рівняння рівноваги:

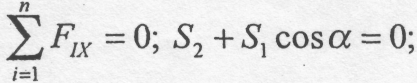
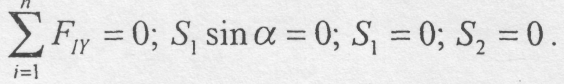
Лема 2. Якщо в ненавантаженому вузлі плоскої ферми сходять­ся три стрижні ,два з яких знаходяться на одній прямій, то зусилля в третьому стрижні дорівнює нулю. Зусилля в перших двох стрижнях рівні між: собою (рис. 5.2, б).

Рівняння рівноваги:

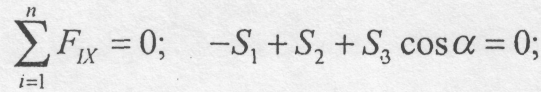
Лема 3. Якщо у вузлі плоскої ферми сходяться два стрижні і до вузла прикладена зовнішня сила, лінія дії якої збігається з віссю одного із стрижнів, то зусилля в цьому стрижні рівне за модулем прикла­деній силі, а зусилля в другому стрижні дорівнює нулю (рис. 5.2, в).

Рівняння рівноваги:

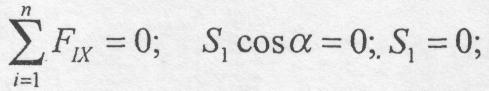
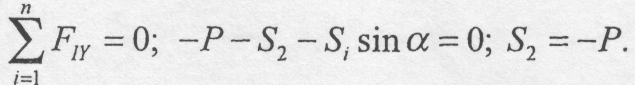
5.2. Визначення зусиль у стрижнях ферми

Обмежимось двома способами визначення зусиль в стрижнях простої ферми: спосіб вирізування вузлів (графічний метод) і спосіб Ріттера (аналітичний метод).

Спосіб вирізання вузлів. Цей спосіб приводить, як до графічно­го, так і до аналітичного розв'язування задачі. Розглянемо його як ме­тод графічний. Метод полягає в тому, що кожний вузол вирізається з ферми і розглядається окремо як вузол, що знаходиться в рівновазі під дією прикладених до нього зовнішніх сил і зусиль розрізаних стриж­нів. Система сил, що діють на вузол являє собою плоску систему збіжних сил, що перебуває в рівновазі, отже, силовий многокутник, побу­дований на цих силах, повинен бути замкнутим.

Побудову силових многокутників слід починати з вузла, утворе­ного двома стрижнями. Тоді побудовою замкнутого трикутника (третя сторона - відома, задана сила, прикладена у вузлі) знайдемо зусилля в цих двох стрижнях. Після цього можна переходити до наступного вуз­ла і т.д. Кожний наступний вузол вибирається так, щоб в ньому сходи­лись не більше двох стрижнів з невідомими зусиллями. Таким чином, графічно будуть визначені зусилля в усіх стрижнях.

Якщо зусилля розрізаних стрижнів направлені по стержнях в бік вузла, то вони є стискаючими, і навпаки - розтягуючими.

Перед тим, як шукати зусилля в стрижнях ферми, слід спочатку знайти реакції опор ферми. З'ясуємо суть графічного методу на при­кладі крокв'яної ферми (рис. 5.3).

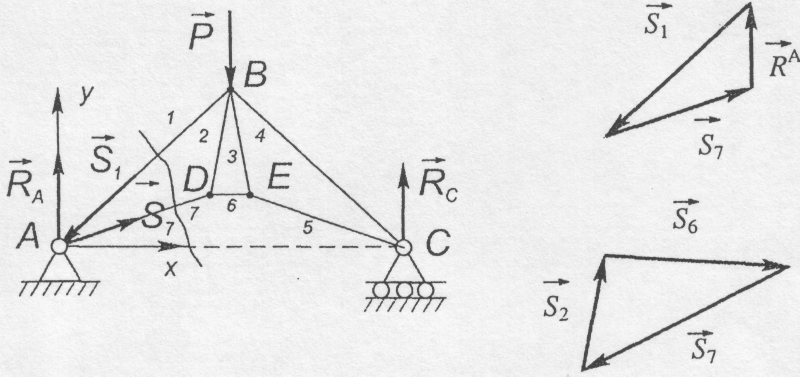
Рис. 5.3

- сила, прикладена у вузлі В.

Розглянемо ферму як тверде тіло, що перебуває в рівновазі під дією плоскої системи паралельних сил: ().

Складемо рівняння рівноваги.

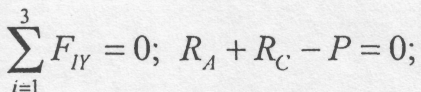
Визначення зусиль почнемо з розгляду вузла А, в якому схо­дяться два стрижні 1 і 7. Будуємо замкнутий силовий трикутник із сил і . З побудованого трикутника знаходимо зусилля і , показуючи ці зусилля у вузлі А, бачимо, що направлено до вузла А, отже воно - стискуюче, а зусилля від вузла А, тобто воно розтя­гуюче. Тепер розглянемо рівновагу сил у вузлі D, в якому сходиться лише два невідомих зусилля і . Реакція стрижня 7, виходячи з вузла D, протилежна за напрямком його ж реакції, що виходить з вузла А. Знову будуємо трикутник сил, починаючи з відомого . Аналогі­чно визначаємо зусилля .

Недоліком цього методу є його громіздкість, тому що необхідно будувати стільки многокутників, скільки вузлів у фермі. Об'єднання розрізнених многокутників сил в одну діаграму здійснили незалежно один від одного англійський фізик Максвел та італійський геометр Кремона, на честь яких цю діаграму названо діаграмою Максвела-Кремони.

Спосіб Ріттера. Цей спосіб дозволяє знайти зусилля в будь-якому стрижні ферми незалежно від зусиль в других стрижнях. Однак, спочатку необхідно визначити реакції опор ферми.

Спосіб полягає в тому, що ферма розсікається на дві частини та­ким чином, щоб в перерізі було не більше ніж три стрижні з невідоми­ми зусиллями. Відкидаємо відсічену частину ферми, і, розглядаючи рівновагу тієї частини, що залишилася, під дією прикладених зовніш­ніх сил і зусиль розсічених стрижнів, одержимо для цієї частини фер­ми три рівняння рівноваги з трьома невідомими зусиллями. Частіше всього ці рівняння є умовами рівності нулю алгебраїчних сум моментів сил відносно трьох різних центрів моментів, за які вибирають точки попарного перетину розсічених стрижнів. Ці точки називаються точ­ками Ріттера.

Якщо з трьох стрижнів - два стрижні паралельні, то одна точка Ріттера віддаляється у нескінченність. Тоді, складають два рівняння моментів сил і одне рівняння алгебричної суми проекцій сил на вісь, перпендикулярну до паралельних стрижнів.

Розглянемо спосіб Ріттера на прикладі розрахунку зусиль в стрижнях ферми, показаної на рис. 5.4:

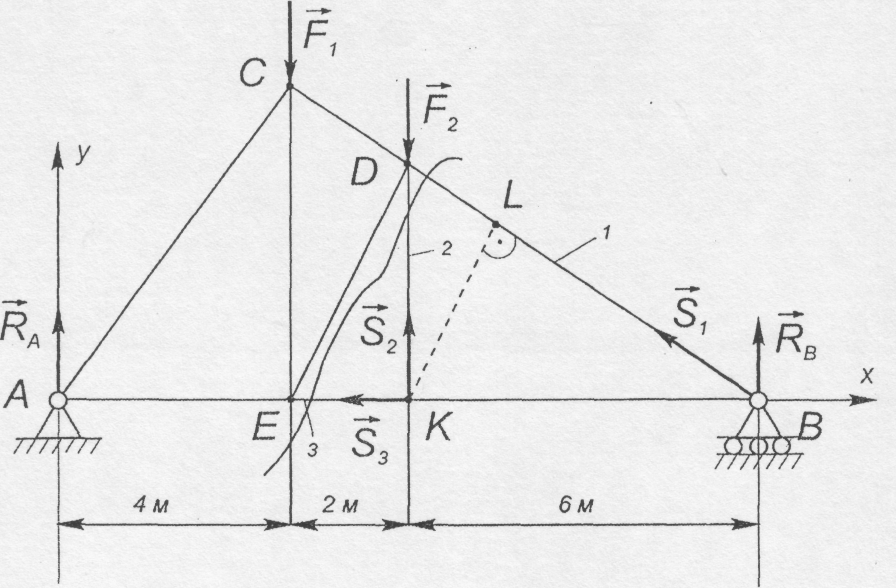
Рис. 5.4

Знайти зусилля в стрижнях ферми 1,2,3, якщо F₁ = 45 кН., F₂ = 20 кН., KD = 2 м, а інші розміри вказані на рис. 5.4.

Розв'язання

Знайдемо реакції в опорах ферми і . Реакція котка В на­правлена по нормалі до опорної площини, а оскільки на ферму діє сис­тема паралельних сил , то й реакція шарніра А буде па­ралельна заданим силам. Щоб визначити ці реакції, складемо рівняння рівноваги системи паралельних сил, що лежать в одній площині у вигляді

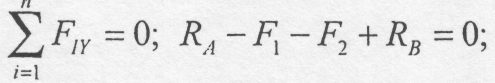
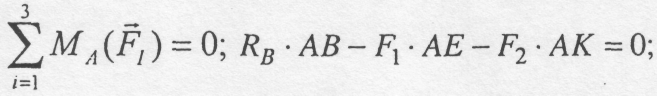
Звідки знаходимо R_A = 40 кН. І R_B = 25 кН.

Проведемо переріз через стрижні 1, 2, 3 і розглянемо рівновагу тієї частини розсіченої ферми, до якої прикладено меншу кількість сил. Це права частина. Зусилля в розсічених стрижнях умовно вважає­мо розтяжним і направимо в бік відкинутої частини.

Отже, у відсіченій частині ферми зрівноважується плоска сис­тема сил . Для визначення зусилля відповідною точ­кою Ріттера буде точка К, а рівняння рівноваги набере вигляду:

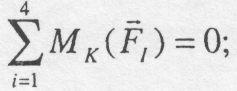
Для визначення зусилля точкою Ріттера є точка В, для ви­значення зусилля - точка D, а відповідні рівняння рівноваги мають вигляд:

Підставляючи необхідні дані, знаходимо

Таким чином, зусилля S₃ - розтягу, S₁ - стиску, S₂ – нульове (при заданому навантаженні стрижень 2 не працює, але з конструкції його викинути не можна, оскільки порушиться жорсткість конструкції і не виконається умова (5.1)).