76

Часть II

I.Функции нескольких переменных

Функции одной переменной не охватывают все зависимости существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных. В качестве примера функций нескольких переменных будем рассматривать функцию двух переменных, т.к. основные особенности таких многоаргументных зависимостей вполне проявляются и в этом случае.

Функция двух переменных

Пусть задано множество D упорядоченных пар чисел (х;у),и соответственно f, которое каждой паре чисел (х;у) сопоставляет только одно число Z, f =Z называется функция двух переменных определенной на множество D и записывается в виде Z= f(х;у). При этом х и у называются независимыми переменными (аргументами),а Z зависимой переменной (функцией)., множество D – называется областью определения функции. Примером такой функции может служить площадь прямоугольника, треугольника и т.д.

Функция двух переменных, как и функции одной переменной может быть задана разными способами (табличный, графический и аналитический). Мы, как правило, будем пользоваться аналитическим способом, когда функция задается с помощью формулы.

1. Предел функции

Э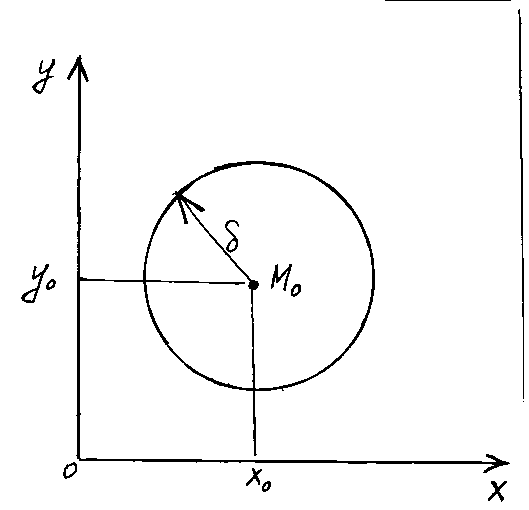то понятие вводится аналогично случаю одной переменной. Для этого надо ввести понятие окрестности точки, (δ-окрестность точки М₀(х₀,у₀)). Это будут все внутренние точки круга с центром в М₀ и радиусом δ. Итак, пусть f(х; у) =.Z определена в некоторой окрестности точки М₀(х₀,у₀), кроме, может быть, этой самой точки. Число А называется пределом Z= f(х; у) при х→х₀ и у→у₀, если для любого >0 существует δ>0, такое, что для всех х≠х₀ и у≠у₀ удовлетворяющих неравенству <δ выполняется неравенство │f(x,y)-A│<. Записывают : или

2. Непрерывность функции двух переменных

Z= f(х; у) называется непрерывной в точке М₀(х₀,у₀), если она:

а) определена в этой точке и некоторой ее окрестности.

б) имеет предел

в) этот предел равен значению функции в точке М_{0, т.е.}

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается, называются точками разрыва этой функции. Точки разрыва могут образовывать целую линию разрыва. Так, функция имеет линию разрыва у=х.

3. Производные и дифференциалы функции нескольких переменных

а) частные производные первого порядка.

Пусть задана функция Z= f(х; у). Т.к. х и у – независимые переменные, то одна из них может меняться, а вторая сохранять свое значение. Дадим х приращение ∆х, сохраняя у=const. Тогда ∆_хZ=f(x+∆x,y)-f(x,y). Аналогично получим ∆_у Z=f(х,у+∆у)- f(x,y). Полное приращение функции ∆Z=f(x+∆x,у+∆y)-f(x,y). Если существует предел , то он называется частной производной функции Z= f(х;у) в точке М(х;у) по переменной х и обозначается Z′_x, ; . Аналогично определяется и частная производная по у Z′=. Все частные производные находятся по формулам и правилам, полученным раннее для функций одной переменной и при условии, что или х или у – считаются const.