курсовая работа / Nat / НАТА_КУРС_1

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ВЕЧЕРНЕ-ЗАОЧНЫЙ

КАФЕДРА УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ

КУРСОВАЯ РАБОТА

по дисциплине

МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ

Выполнил: ст. гр. УИТ-51в

Корнилова Н.В.

Принял:

Мефёдова Ю.А.

Балаково 2004 г.

СОДЕРЖАНИЕ

Исходные данные . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	3
ВВЕДЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	4
ОСНОВНЫЕ ПОНЯТИЯ	5
Основные понятия СРП . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	5
3. Идентификация вида д.у . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	9
4. Определение континуальной передаточной функции . . . . . . . . .. .	10
5.Определение выходной величины. . . . . . . . . . . . . . . . . . . . . . . . . . .	11
6.Синтез интегральной передаточной функции.. . . . . . . . . . . . . . . . .	15
7. Построение ЛАЧХ и ЛФЧХ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	17
8. Аппроксимация полученных характеристик . . . . . . . . . . . . . . . . . .	18
Список использованной литературы . . . . . . . . . . . . . . . . . . . . . . . . . .	20

ИСХОДНЫЕ ДАННЫЕ

;

;

; ; ; ;

;

;

;

ВВЕДЕНИЕ

Система с распределенными параметрами (СРП) – это система, в которой практически все сигналы (особенно входной и выходной) зависят от пространственных координат и времени.

Есть среды, которые не могут быть описаны в сосредоточенных параметрах (электромагнитное поле, электростатическое поле, течение потока, гравитационное поле, температура и т.д.).

Система с сосредоточенными параметрами является частным случаем СРП и вводится для упрощения и решения задач на первом (нулевом) этапе.

Практически все природные явления и функции могут быть описаны семью дифференциальными уравнениями в частных производных.

В данной курсовой работе решается вопрос построения математической модели элемента на основе теории распределенных сигналов.

Цель работы – синтез интегральной передаточной функции для объектов управления с распределенными параметрами.

ОСНОВНЫЕ ПОНЯТИЯ СРП.

Основной характеристикой СРП является континуальная передаточная функция. Она показывает отношение выходной функции к входной (по Лапласу) в привязке к конкретной точке.

В искомой задаче выходная функция обозначается буквой Q(х,t), где x - трехмерная переменная в декартовых, полярных, цилиндрических или сферических координатах, f(x,t) - входная координата по среде, зависящая от трехмерной координаты х и времени t. Основное уравнение задачи записывается в виде:

l(Q(х,t)) = f(х,t), xD, t≥t₀,

где l - оператор дифференциального уравнения - формула преобразования выходной величины Q.

В каждой задаче определяются граничные или краевые условия:

Г(Q(х,t))=g(х,t); xD, t>t₀,

где Г - оператор граничных или краевых условий, g - входное воздействие на границе в каждый момент времени.

Для того чтобы решить задачу во всей области координат, необходимо знать ее значения в каждой точке по границе области.

Начальные условия для задачи записываются в виде

N(Q(х,t))= Q₀(х); xD, t=t₀,

где N - оператор начальных условий; Q₀(х) - значение искомой функции в заданный момент времени.

Для того чтобы решить задачу во всей области координат, необходимо знать её значения в каждой точке пространства x. Получили систему:

l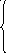(Q(х,t)) = f(х,t), xD, t≥t₀,

Г(Q(х,t))= g(х,t); xD, t>t₀, (1)

N(Q(х,t))= Q₀(х); xD, t=t_0.

Необходимо знать:

1 Значение функции на границе в каждый момент времени

2 Значение в каждой точке области в момент времени t₀.

В указанном виде (1) система практически не разрешима. Для ее решения вводится в рассмотрение стандартная форма записи (2). Она подразумевает нулевые граничные и начальные условия. Ее вид:

l(Q(х,t)) =ω(х,t), xD, t≥t₀,

Г(Q(х,t))=0; xD, t>t₀, (2)

N(Q(х,t))=0; xD, t=t₀,

где ω(х,t) - стандартизующая функция ω(х,t)= f(х,t)

При Г=0, N=0 - входное воздействие на систему при нулевых граничных и начальных условиях и первая из трех основных функций, которая понадобится при решении (берется из справочника).

Второй функцией является функция Грина (импульсная переходная функция, функция влияния, функция источника, функция веса). Функцией Грина называется функция источника, которая равна выходному сигналу G(x,t) = Q(x,t) при f(х,t)= δ(х - ξ) δ(t - τ), где δ(х - ξ) - пространственная δ-функция по координатам x,y,z, δ(t - τ) - функция по времени; х - координаты входного возмущения; ξ- координаты точки отклика от удара.

С учетом этого стандартная задача (2) перепишется в виде:

l(G(х,ξ,t,τ)) = δ(х - ξ) δ(t - τ),

Г(G(х, ξ,t,τ))=0; (3)

N(G(х, ξ,t,τ))=0;

где функция Грина от G(x,t) берется из справочника.

Зная эти две характеристики можно найти выходную функцию по следующему выражению:

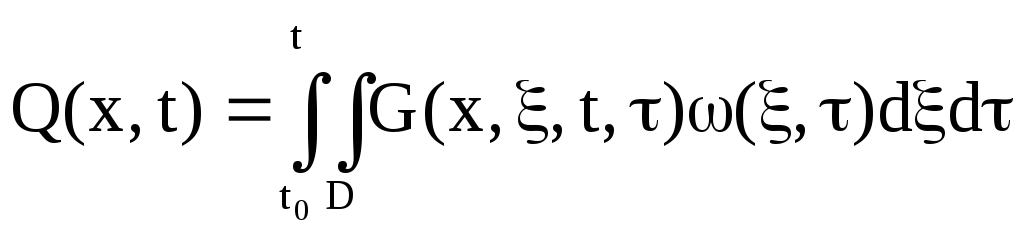(4)

Е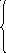сли задача статическая, то есть отсутствует уравнение времени t, то ее можно записать в виде

l(Q(х)) = f(х), xD,

Г(Q(х))= g(х); xD, (5)

N≡0_.

Стандартная форма записи будет выглядеть как:

l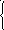(Q(х)) = ω(х), xD,

Г(Q(х))= 0; xD, (6)

при однородных (нулевых) граничных условиях.

Ф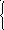ункция Грина такой задачи удовлетворяет системе уравнений:

l(G(х,ξ)) = δ(х - ξ) δ(t - τ), xD, ξD,

Г(G(х,ξ))=0; (7)

х- координаты возмущения, ξ - координаты отклика.

Решение задачи в этом случае выглядит следующим образом

(8)

Бывают задачи, в которых отсутствуют пространственные координаты, т.е. процесс во времени. В таком случае задача записывается следующим образом:

l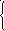(Q(t)) = f(х,t), xD, t≥t₀,

N(Q(t))= Q₀. (9)

Стандартная форма записи:

l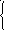(Q(t)) = ω(t), t≥t₀,

N(Q(t))=0. (10)

Функция Грина:

l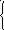(G(t,τ)) = δ(t - τ),

N(G(t,τ))=0; (11)

Решение такой задачи имеет вид:

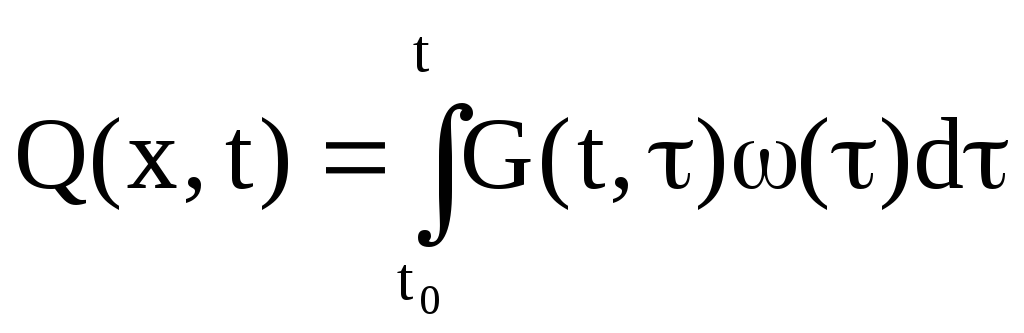(12)

Для управления и синтеза системы управления, исходя из ТАУ, необходимо знать передаточную функцию. В теории СРП вводится понятие континуальной передаточной функции, т.е. точечной передаточной функции в пределах области D, когда возмущение подается на среду в точке х, а реакция регистрируется в точке ξ.

Континуальная передаточная функция выражается следующим образом:

(13)

По сути, континуальная передаточная функция - это преобразование Лапласа функции Грина, т.е. при этих функциях континуальная передаточная функция является производной и всегда может определиться по функции Грина.

Таким образом, для решения задачи по CРII необходимо знать две функции: нормирующую функцию и функцию Грина

Теория СРП включает структурный метод ТАУ, который подразумевает операции с распределенными блоками: если блоки соединяются последовательно; если блоки соединяются параллельно; при включении второго блока в обратную связь. В связи с этим вводится понятие операторного изображения выходной величины. В теории распределенных блоков выходная величина определяется следующим образом:

, (14)

где - изображение по Лапласу выходной величины решаемой задачи; - континуальная передаточная функция; - изображение по Лапласу нормирующей функции.

Если удается из нормирующей функции выделить в явном виде компоненту входной координаты с помощью специальных средств или методов

, (15)

то уравнение (14) перепишется в виде:

, (16)

С помощью двух способов (коэффициент разложения и коэффициент приближения) по возможности выносится входное возмущение (по Лапласу) за знак интегрирования, получим:

(17)

Полученное выражение (17) - отношение изображения по Лапласу выходной величины к изображению по Лапласу входного возмущения, как интеграл по области D континуальных функций, называется интегральной передаточной функцией (функция Власова В.В.).

ИДЕНТИФИКАЦИЯ ДУ.

Проведем идентификацию уравнения:

(*)

Данное уравнение относится к параболическому типу и описывает трехмерную задачу в декартовых координатах. Уравнения параболического типа содержат первую производную по времени t и вторую производную по пространственным координатам х, y, z. Они описывают задачи, связанные с процессами теплопроводности, диффузии, с распространением электромагнитных волн, с движением вязкой жидкости. Уравнение (*) является неоднородным уравнением теплопроводности, учитывающее внешнее воздействие от внутренних источников вещества или энергии.

В начале расчета необходимо определить физический смысл выходной величины Q, входного возмущения f и координат x ,y, z, и t .

Предположим, что данное уравнение описывает процесс нагрева бруса.

Входным возмущением является поток тепла от нагревательного элемента, приложенного к брусу. Пусть воздействие изменяется по косинусоидальному закону, а именно:

, где А-амплитуда, ω- частота, равная 2.

(,) – входные координаты

(x,y,z) – выходные координаты

 изменяется в пределах 0    a.

изменяется в пределах 0   b.

изменяется в пределах 0  c.

Q – выходная величина, соответствующая температуре бруса после воздействия на него теплового потока.

Начальные условия с учетом этих допущений запишутся в виде:

, что соответствует температуре бруса в начальный момент времени.

Так как процесс исследуется в неограниченном пространстве, то граничные условия отсутствуют.

Тогда стандартизирующая функция запишется в виде

ОПРЕДЕЛЕНИЕ КОНТИНУАЛЬНОЙ ФУНКЦИИ.

Континуальная передаточная функция выражается следующим образом:

В данном варианте континуальная функция задана:

;

ОПРЕДЕЛЕНИЕ ВЫХОДНОЙ ВЕЛИЧИНЫ.

Выходная величина находится по формуле:

, где

,

Пусть a=b=c=10, тогда

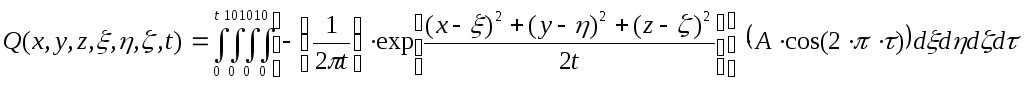
Вычислим этот интеграл, используя программу Mathcad 11.

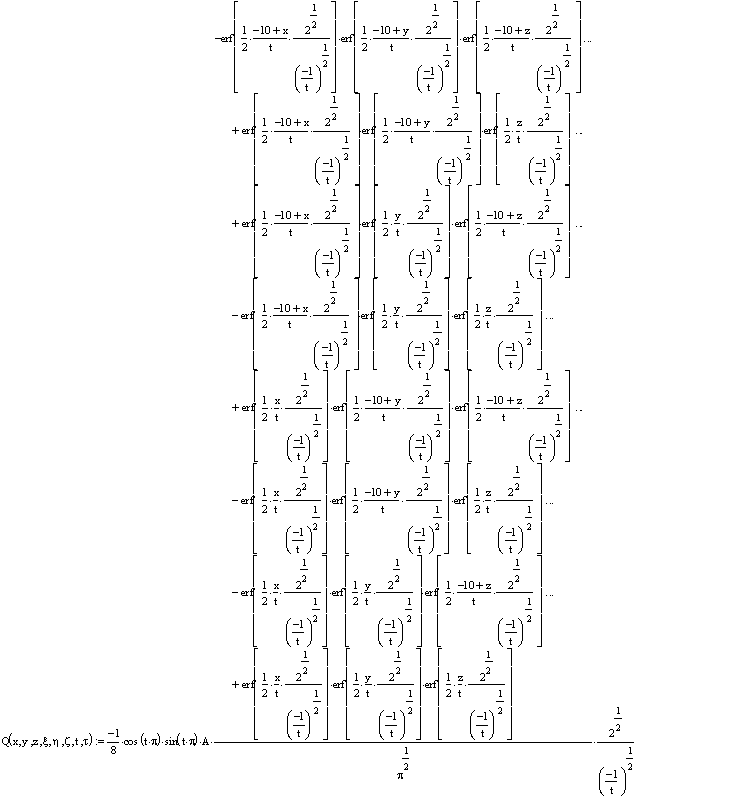
где erf (x) – функция ошибок или интеграл вероятности или функция Крампа

Построим динамическую характеристику. Для этого зададимся определенными значениями координат x, y, z, а также зададим интервал изменения времени t.

Пусть

С учетом этого рассчитаем интеграл:

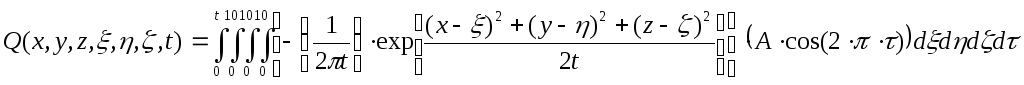
Получим:

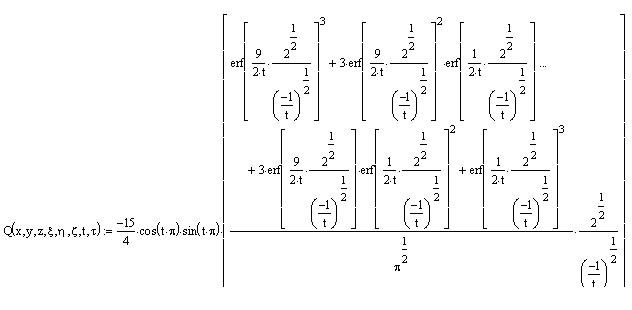
Или

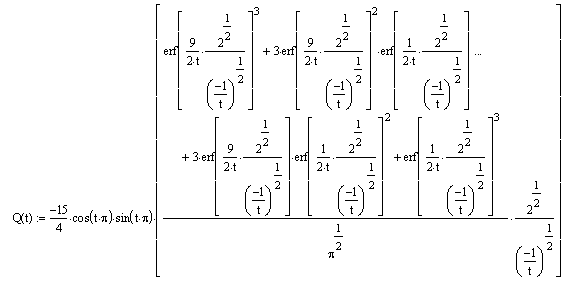
Построим динамическую характеристику, то есть зависимость Q(t)

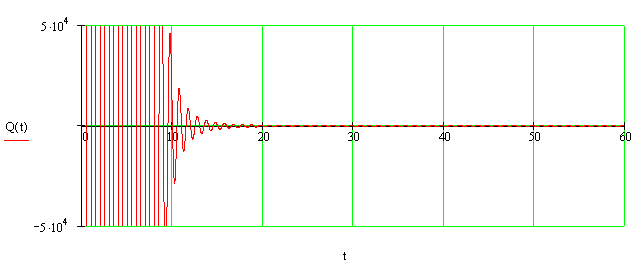
СИНТЕЗ ИНТЕГРАЛЬНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ

Для определения интегральной передаточной функции необходимо найти операторное выражение выходной величины, которое будет иметь вид .

Для дальнейших вычислений необходимо определить изображение по Лапласу нормирующей функции по формуле:

Выделим из нормирующей функции в явном виде компоненту входной координаты:

, то есть

Таким образом, операторное изображение выходной величины запишется:

;

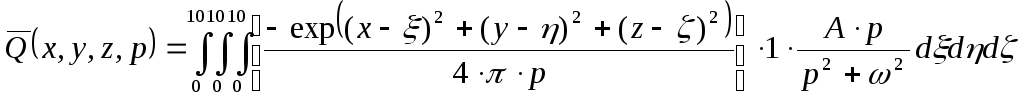Интегральная передаточная функция определяется по формуле:

или

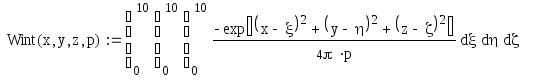
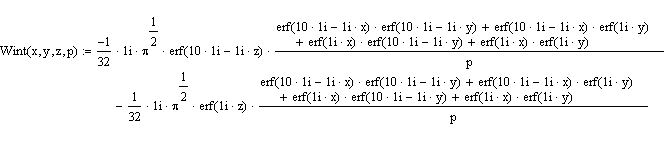
Определим значение интегральной передаточной функции в точке с координатами (5,5,5), то есть:

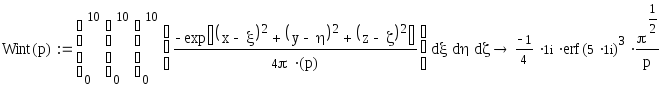
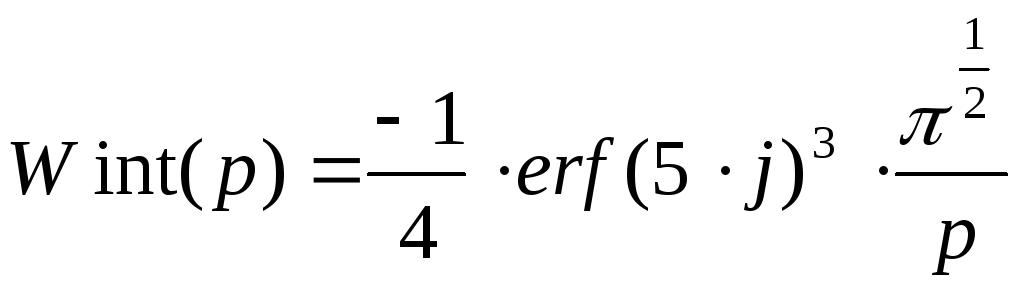
Таким образом, получили интегральную передаточную функцию, которая соответствует передаточной функции интегрирующего звена W(p).

ПОСТРОЕНИЕ ЛАЧХ И ЛФЧХ.

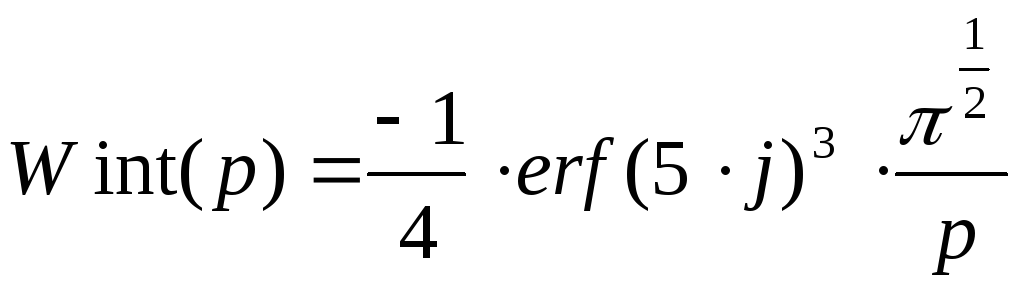
Заменим оператор р на j, где получим:

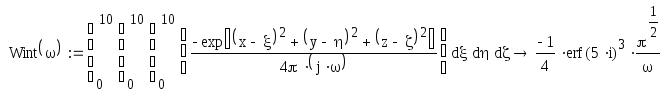
Разделим полученное выражение на действительную и мнимую части:

;

.

Логарифмическая амплитудно-частотная характеристика определяется по формуле:

Логарифмическая фазочастотная характеристика находится по формуле:

По полученным данным строим графики ЛАЧХ и ЛФЧХ. (рисунок 1 и рисунок 2)

.

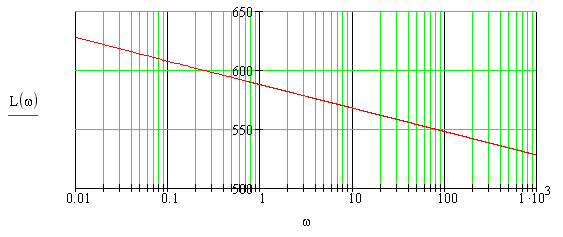
Рисунок 1. ЛАЧХ

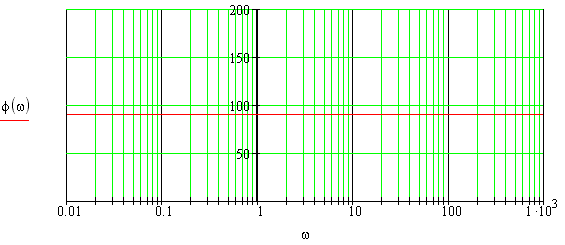
Рисунок 2. ЛФЧХ

АППРОКСИМАЦИЯ ХАРАКТЕРИСТИК.

Аппроксимируем полученные характеристики стандартными типовыми наклонами и запишем выражение аппроксимированной передаточной функции.

Определим статический коэффициент передачи:

20logK=588,07 K=2,53

С помощью аппроксимации передаточная функция запишется в виде:

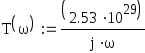
В результате выполнения курсовой работы была получена передаточная функция объекта с распределёнными параметрами. Кроме того, было рассмотрено распределенное возмущающее воздействие и найдена реакция объекта на него.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Бутковский А.Г. Характеристики систем с распределенными параметрами. – М.: Наука, 1979. –224с.

2. Власов В.В. Синтез интегральной передаточной функции для объектов управления с распределенными параметрами // Школа академика Власова: Сб. метод. тр. – М.: Буркин, 1998. – 128с.

3. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.: Наука. 1966. -992с.

4. Топчеев Ю.И. Атлас для проектирования систем автоматического регулирования. М.: Наука. 1989. –752с.

5. Чемоданов Б.К., Иванов В.А., Медведев В.С., Ющенко А.С. Математические основы теории автоматического регулирования. Том 1 – М.: Высшая школа, 1977. -366с.

20