курсовая работа / Емкостной датчик / KursovikSRP / курсовикСРП

ВВЕДИНИЕ

Моделирование – процесс замещения объекта исследования некоторой его моделью и проведение исследований на этой модели с целью получения необходимой информации об исследуемом объекте.

Различают два типа моделирования: предметное и абстрактное.

При первом способе моделирования строят физическую модель, соответствующим образом отражающую основные физический свойства и характеристики моделируемого объекта. При этом модель может иметь другую физическую природу, по сравнению с реальным объектом.

При абстрактном моделировании используют множество видов математических моделей, представляющие собой совокупность математических объектов и отношений между ними, адекватно отражающих физические свойства создаваемого технического объекта. В общем случае уравнение математической модели связывает физические величины, характеризующие состояние объекта.

Модель – физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие физические свойства и характеристики моделируемого объекта.

Процесс моделирования включает в себя несколько этапов:

• постановка задачи и определение свойств реального объекта, подлежащего исследованию;

• констатация затруднительности или невозможности реального объекта;

• выбор модели, хорошо описывающей основные свойства объекта, с одной стороны, и легко поддающаяся исследованию, с другой;

• исследование модели в соответствии с поставленной целью;

• проверка адекватности объекта и модели; если соответствий нет, то необходимо повторить п. а – г.

1 ИСХОДНЫЕ ДАННЫЕ

Рассчитать изменение сопротивления медного проводника ТСМ50. Идентифицировать тип дифференциального уравнения. По заданному дифференциальному уравнению получить выражение для передаточной функции в распределенных параметрах, выражение для выходной величины. Построить статическую характеристику выходной величины, а также логарифмические характеристики.

Исходные данные:

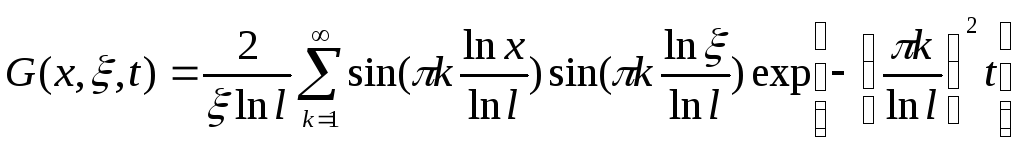
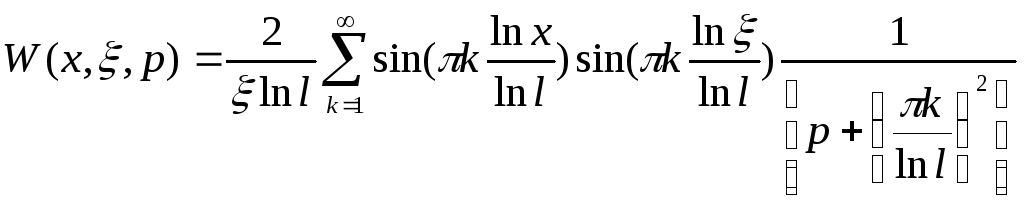
2 ОСНОВНЫЕ ПОНЯТИЯ СРП

Первый этап в развитии ТАУ связан с управляемыми системами состояния, которые характеризуется поведением во времени t некоторого набора функций одной переменой t конечного числа n:

(1)

Подобные системы обычно описываются обыкновенными дифференциальными уравнениями или системами дифференциальных уравнений относительно g(t) и называются системами с сосредоточенными параметрами. Модели большого числа объектов управления могут быть с достаточной для практической точности точностью ССП. По практике любой технический объект имеет вполне определенные геометрические размеры, поэтому функция характеризующая ее состояние изменяется в пределах пространственной области и следовательно зависит не только от времени, но и от пространственных координат.

Такие системы называются системы с распределенными параметрами. Состояние СРП описывается дифференциальным уравнением с частыми производными, интегральными уравнениями, а также гибридными. Функция состояния Q(x,t) определенная на пространственной области Д удовлетворяет уравнению:

L[Q(x,t)]=f(x,t) , t>0 (2)

где Д- открытая часть области Д не содержащая границы;

L- некоторый заданный оператор(функция в частных производных);

f(x,t)- известная функция характеризующая внешнее воздействие на процесс.

Если , то (2) – однородное уравнение,

, то (2)- неоднородное уравнение.

Если g(x,t)- векторная функция состояния , то (2)-представляет собой систему уравнений.

Для получения единственного решения уравнения (2) необходимо дополнить начальными условиями, которые описываются некоторым линейным оператором

N[Q(x,t)]=Q(x,t) , t=0 (3)

Полная система уравнений должна содержать граничные условия от Q(x,t) которые характеризуют взаимодействие Q(x,t) с внешней средой должно выполнятся условие t>0 на границе области Д.

(4)

где Г- линейный оператор;

- внешние воздействие, которое можно рассматривать как второй вход объекта наряду с .

Если , то граничное условие однородное и наоборот.

Уравнения математической физики являются основой для построения математической модели элементов систем уравнений с распределенными параметрами. Для их практического применения основной сложностью является выбор уравнения, который могло бы с заданной точностью и степенью достоверности описать интересующий элемент системой управления.

Самостоятельно составлять и получать в частных производных является сложной задачей, поэтому используют следующий алгоритм:

1) Выбирается система координат исходя из конструкции элемента СУ.

2. Выбирается размерностьr пространственной области D определения функции Q данной задачи.

3. Наивысший порядок производных m функции Q по независимой временной производной t ограничивается двойной.

4. Наивысший порядок производных n функции Q по пространственным переменным ограничивается двойной.

5. Выбирается дифференциальное уравнение группы ( r, m, n) в нужной системе координат.

6. Уравнение «офизичивается», то есть производится конструирование размерностей. Это означает, что задается первичная размерность, либо входному возмущению f (x, y, z, t ), либо выходному сигналу Q (x, y, z, t ). В зависимости оттого, что интересует. Далее рассчитываются вторичные размерности исходя из конкретного вида уравнения и зависящая от первичных размерностей.

7. Находится выходной сигнал и производится его сопоставление с ожидаемыми результатами.

8. Если результат не устраивает, выбираем другое уравнение и повторяем все процедуры заново.

Во многих случаях для описания физических процессов используют уравнений с частыми производными до второго порядка включительно.

Так, например, процессы распространения тепловой энергии описывается уравнением теплопроводности

,

где и С – плотность и теплоемкость вещества,

Т- температура,

k- коэффициент теплопроводности,

Q – плотность источника тепла.

Анализ стационарных состояний, например, статических тепловых, электрических, магнитных полях проводят, используя уравнение Пуассона

где u(x, y, z) – функция, описывающая статическое поле,

f( x, y, z)- распределенные источники.

Несмотря на различие процессов, все они могут быть представлены как частные случаи обобщенной формы дифференциального уравнения второго порядка.

Рассмотрим уравнение второго порядка с двумя независимыми переменными x и y:

(1)

где A,B,C,D- некоторые функции, зависящие в общем случае от x, y,u.

На основании того, что уравнение 1 можно поставить в квадратичную форму

по природе различают следующие типы квазилинейных уравнений:

1. гиперболический, если В²-4АС>0- его аналогом является волновое уравнение;

2. параболический, В²-4АС=0-его аналог уравнение теплопроводности;

3. эллиптический, если В²-4АС<0- аналог уравнение Пуассона или Лапласа.

3 ИДЕНТИФИКАЦИЯ ТИПА ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

ЗАДАНИЕ ВХОДНОГО И ВЫХОДНОГО ПАРАМЕТРОВ, НАЧАЛЬНЫХ И ГРАНИЧНЫХ УСЛОВИЙ

Так как данное дифференциальное уравнение содержит первую производную по времени, то оно относится к параболическому типу. Также это уравнение является неоднородным.

Выходным параметром Q(x,y,t) в данной системе является сопротивление медной проволоки.

Входным воздействием f(x,y,t) является поток тепла от корпуса термопреобразователя сопротивления ТСМ50.

Рисунок 1- Вид входного воздействия

Граничные условия:

Зададим размерность входного возмущения.

,

где F- количество теплоты (теплой поток)

V-объем.

– удельная теплоемкость меди.

- плотность меди.

-коэффициент теплопроводности,

где -коэффициент теплопроводности меди.

Тогда а² =0.884 м²/с.

Пусть l₁ = 18 – длина проволоки.

Начальные условия:

, что соответствует сопротивлению ТСМ50 до начала действия теплового потока.

Граничные условия:

, что соответствует изменению сопротивления в начале проволоки.

- что соответствует изменению сопротивления на конце проволоки.

С учетом выше описанных условий стандартизирующая функция примет следующий вид:

4 РАСЧЕТ ВЫХОДНОЙ ВЕЛИЧИНЫ

Для определения вида статической характеристики воспользуемся функцией Грина:

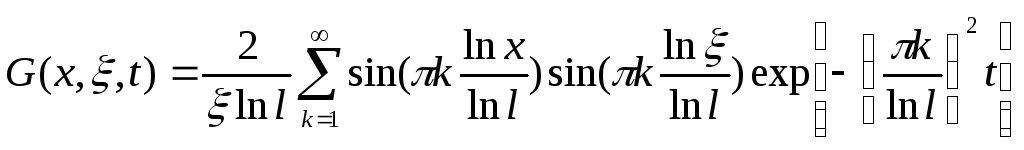
Для этого первоначально произведем расчет выходной вылечены по формуле:

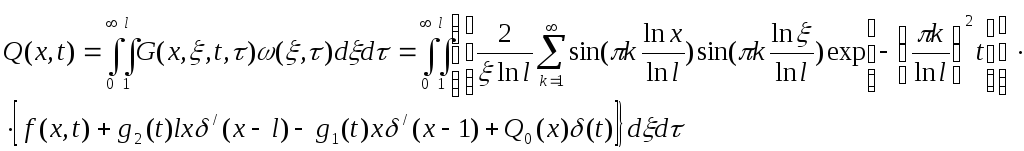
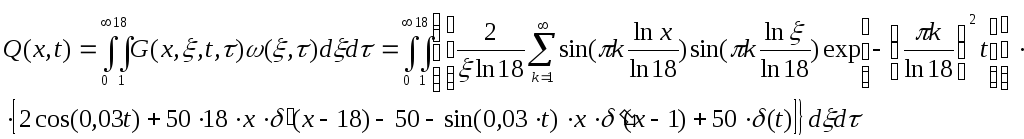
Ввиду явной неразрешимости интеграла, в котором присутствует сумма ряда до бесконечного члена, введем ограничение на количество рядов 1, т.е. возьмем первый член ряда. Эта мера является вынужденной и ведет к большой погрешности.

Таким образом, учитывая принятые меры, получим уравнение:

Используя свойства  - функции для упрощения уравнения, построим статическую характеристику выходной величины при фиксированных значениях координаты и времени.

а

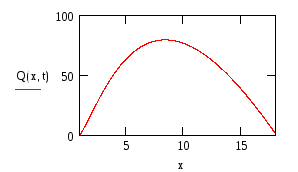
б

Рисунок – 2 Статическая характеристика выходного сигнала: а - при фиксированном значении координаты; : б - при фиксированном значении времени.

5. РАСЧЕТ ИНТЕГРАЛЬНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ.

ПОСТРОЕНИЕ ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК

Найдем изображение по Лапласу стандартизирующей функции.

Выделим в явном виде компоненту входной координаты.

Выражение для имеет следующий вид:

Интегральная передаточная функция определяется выражением

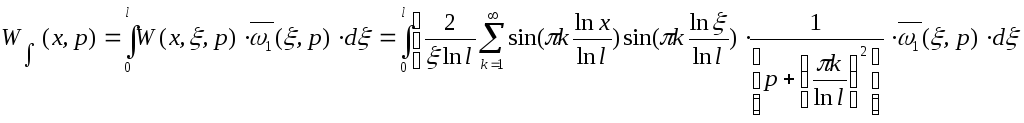
Проведя интегрирование и все преобразования, получим следующее выражение для интегральной передаточной функции:

Для построения ЛАЧХ в полученной интегральной передаточной функции заменим р на jω и затем воспользуемся формулой:

Выполним расчет и построение ЛАЧХ с помощью программы Matchcad 2000, задав произвольно необходимые параметры:

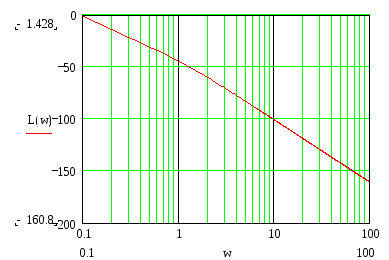
Рисунок 3- ЛАЧХ.

ЗАКЛЮЧЕНИЕ

В данной курсовой работе был произведен расчет системы с распределенными параметрами: изменение сопротивления медной проволоки по длине. В ходе расчетов было выявлено ниже следующее.

Система устойчива, имеет высокие качественные характеристики и достаточный коэффициент усиления. Данная система не требует дальнейшей доработки. Это означает, что были правильно подобраны начальные, граничные условия и дифференциальное уравнение для описания данной системы.

СПИСОК ЛИТЕРАТУРЫ

1. Тарасик В.П. Математическое моделирование технических систем: Учебник для вузов.-МН.: ДизайнПРО, 2004.

2. Бутковский А.Г. Характеристики систем с распределенными параметрами. – М.: Наука, 1979. –224с.

3. Арсенин В. Я. Математическая физика. – М. Наука, 1966.

17

УИТС.ХХХХХХ.007 КР