курсовая работа / аодв / panther-2я часть!!!

Содержание

Содержание 2

Задание на работу 3

Введение 5

Основная часть 6

1. Идентификация дифференциального уравнения 6

2. Записать выражение для выходного сигнала 8

3. Синтез интегральной передаточной функции 10

4. Построение ЛАЧХ и ФЧХ и их апроксимация 11

Вывод 14

Список используемых источников 15

Задание на работу

Дифференциальное уравнение имеет вид:

Граничные условия:

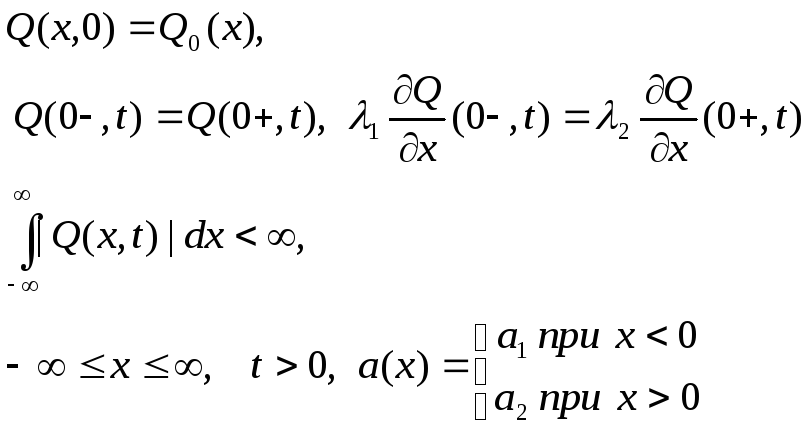
Начальные условия: Q₀(x) = 0, ₁=1, ₂=1, а₁ = 2 а₂ = 1,

f(x,t) = 10⁶, x = 0,05,

Нормирующая функция:

Функция Грина имеет вид:

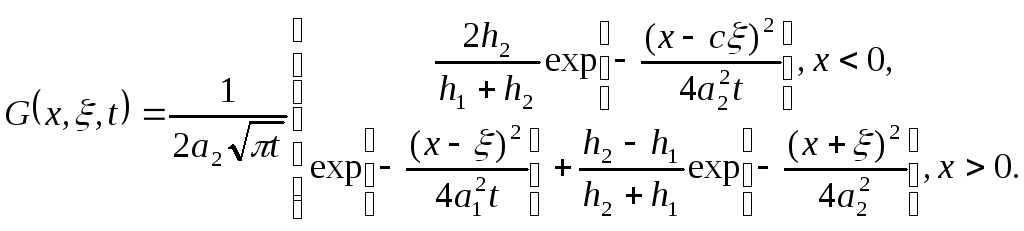
где

Континуальная передаточная функция имеет вид:

.

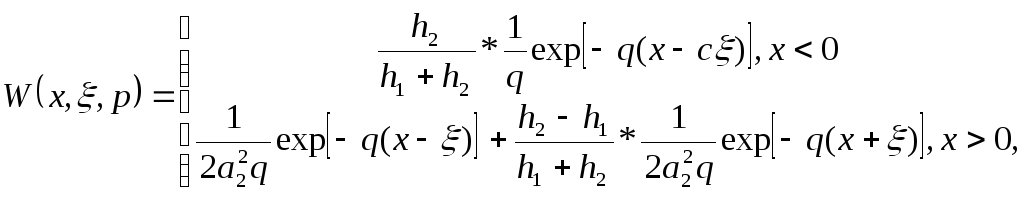где - температура составного неограниченного стержня

По заданному дифференциальному уравнению объекта получить выражение для передаточной функции в распределенных параметрах, выражение для выходной величины, выражение для оценочной передаточной функции для наилучших условий управления. Построить оценочную ЛАЧХ, аппроксимировать ее с погрешностью 5%, записать выражение передаточной функции через типовые звенья.

Введение

Система с распределенными параметрами (СРП) – это система, в которой практически все сигналы (особенно входной и выходной) зависят от пространственных координат и времени.

Есть среды, которые не могут быть описаны в сосредоточенных параметрах (электромагнитное поле, электростатическое поле, течение потока, гравитационное поле, температура и т.д.).

Система с сосредоточенными параметрами является частным случаем СРП и вводится для упрощения и решения задач на первом (нулевом) этапе.

Практически все природные явления и функции могут быть описаны семью дифференциальными уравнениями в частных производных.

В данной курсовой работе решается вопрос построения математической модели элемента на основе теории распределенных сигналов.

Цель работы – синтез интегральной передаточной функции для объектов управления с распределенными параметрами.

Основная часть

1. Идентификация дифференциального уравнения

По виду дифференциального уравнения определяем, что данное уравнение параболического типа.

Процессы распространения тепла или диффузии частиц в среде описываются общим уравнением диффузии:

.

Выведем уравнение распространения тепла. Обозначим через u(x, t) температуру среды в точке х = (х₁, х₂, х₃) в момент времени t. Считая среду изотропной, обозначим через (х), с(х) и k(х) соответственно ее плотность, удельную теплоемкость и коэффициент теплопроводности в точке х. Обозначим через F(х, t) интенсивность источников тепла в точке х в момент времени t. Подсчитаем баланс тепла в произвольном объеме V за промежуток времени (t, t+t) . обозначим через S границу V, и пусть n – внешняя нормаль к ней. Согласно закону Фурье через поверхность S в объем V поступает количество тепла

,

равное, в силу формулы Гаусса-Остроградского,

.

За счет тепловых источников в объеме V возникает количество тепла:

.

Так как температура в объеме V за промежуток времени (t, t+t) выросла на величину

,

то для этого необходимо затратить количество тепла

.

С другой стороны Q₃ = Q₁+Q₂ и потому

,

откуда, в силу произвольности объема V, получаем уравнение распространения тепла:

Если среда однородна, т. е. с, р и k — постоянные, то уравнение принимает вид:

где

Уравнение (13) называется уравнением теплопроводно­сти. Число п пространственных переменных х₁, х₂,..., х_п в этом уравнении может быть любым.

Как и в случае уравнения колебаний, для полного описания процесса распространения тепла необходимо задать начальное распределение температуры и в среде (начальное условие) и режим на границе этой среды (граничное условие).

Примеры граничных условий:

а) Если па границе S поддерживается заданное распределение тем­пературы и₀, то

u|_s = и₀.

b) Если на S поддерживается заданный поток тепла и₁, то

с) Если па S происходит теплообмен согласно закону Ньютона, то

где h — коэффициент теплообмена и и₀ — температура окружающей среды.

Аналогично выводится и уравнение диффузии частиц. При этом вместо закона Фурье нужно пользоваться за­коном Нэрнста для потока частиц через элемент поверх­ности ΔS за единицу времени:

где D(x) —коэффициент диффузии и и(х, t) — плотность частиц в точке х в момент времени t. Уравнение для плотности и будет иметь вид (11), где ρ обозначает ко­эффициент пористости, ρ = D и q характеризует погло­щение среды.

2. Записать выражение для выходного сигнала

По заданной функции Грина и стандартизирующей функции можно определить функцию для выходного сигнала:

.

.

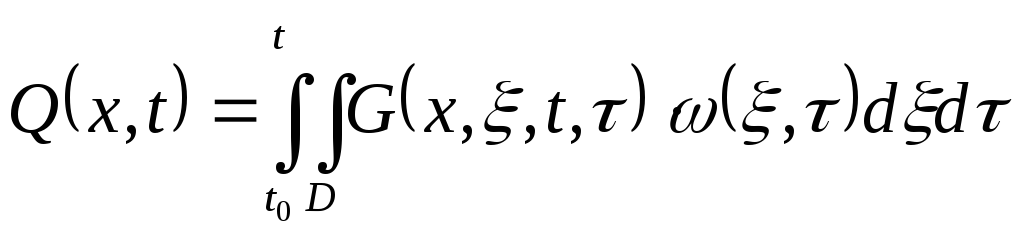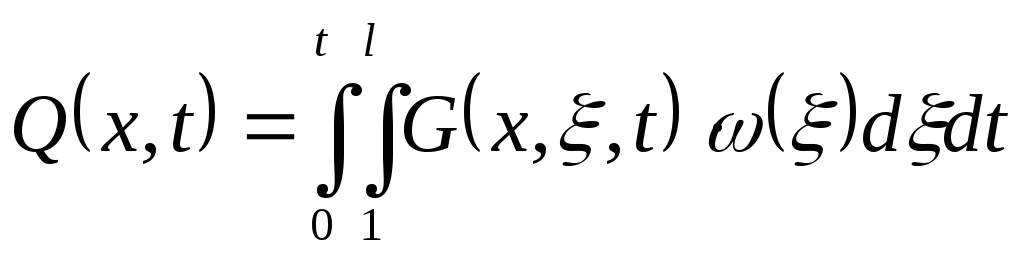Для нахождения данного интеграла упростим нормирующую функцию и функцию Грина, подставив заданные значения, получим:

Подставим полученные выражения в уравнение по нахождению двойного интеграла и вычислим интеграл по координате и по времени:

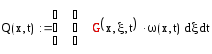
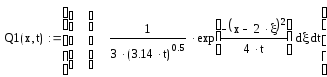
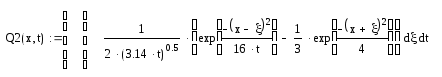
Интегрируя данные выражения, получаем

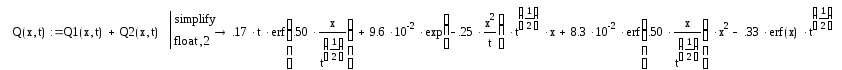
Если координата х величина постоянная (х = 0,05),

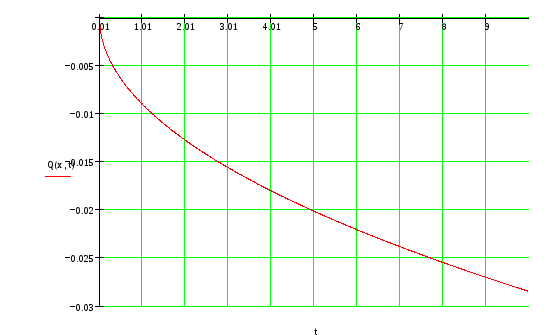
График 1 – Зависимость выходной функции от времени

Если время t величина постоянная (t = 3), то можно записать

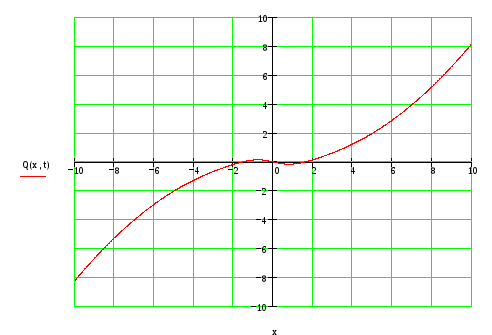
График 2 – Зависимость выходной функции от координаты

3. Синтез интегральной передаточной функции

1. Определим изображение по Лапласу нормирующей функции.

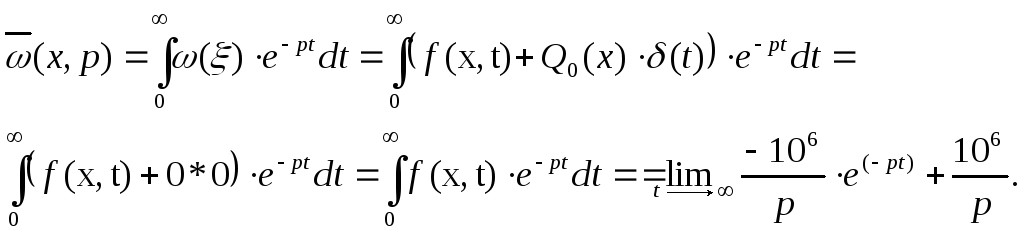
Так как exp^∞ = 0 , то нормирующая функция примет вид:

2. Запишем входную функцию в изображении по Лапласу:

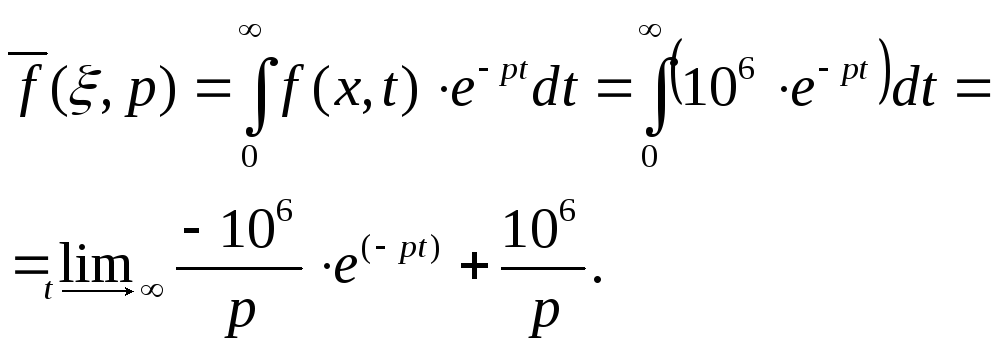
Так как exp^∞ = 0 , то входная функция примет вид:

3. Найдем отношение изображения по Лапласу нормирующей функции к входной функции изображения по Лапласу:

4. Выведем отношение выходной величины по Лапласу Q(ξ, p) к входной величине по Лапласу f(ξ, p), т.е. найдем функцию Власова.

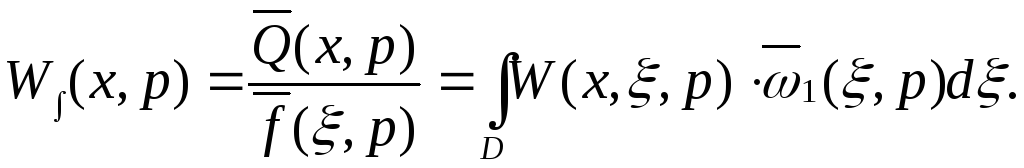
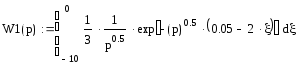
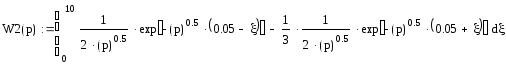
5. Производим замену p на jω:

6. С помощью MathCada выделяем в этой функции мнимую и действительную части:

где и

4. Построение ЛАЧХ и ФЧХ и аппроксимация

По полученной функции построим ЛАЧХ и ФЧХ.

График аппроксимируем по типовыми звеньям, передаточные функции: и

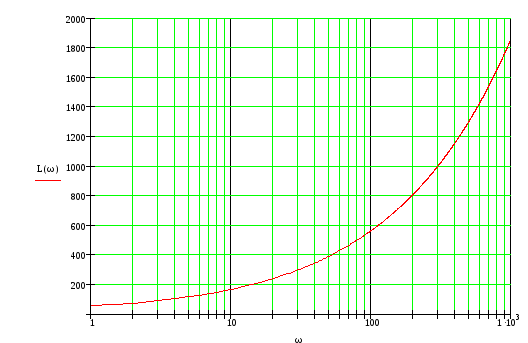
1 частота среза ₁ = 10

2 частота среза ₂ = 100

T₁ = 1/₁ = 0,1

T₂ = 1/₂ = 0,01

Определим k, при  = 0

20*lgk = 34 дб

k = 52.

1 наклон равен 400 дб/декаду, следовательно степень 1го типового звена равна 20

2 наклон равен 1300 дб/дек, следовательно степень 2го типового звена равна 65

Производим замену p на jω:

С помощью MathCada выделяем в этой функции мнимую и действительную части и строим ЛАЧХ:

где и

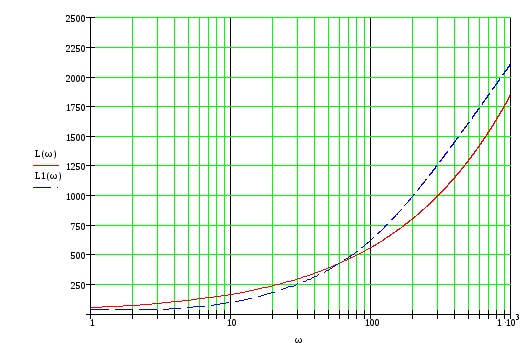
Фактическая и аппроксимированная ЛАЧХ

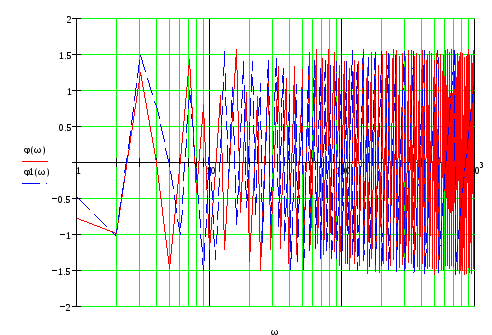
Фактическая и аппроксимированная ФЧХ

Вывод

В данной работе мы провели идентификацию заданного дифференциального уравнения. Получили уравнение теплопроводности параболического типа.

Мы синтезировали интегральную передаточную функцию. В результате получили некоторую передаточную функцию, с помощью которой построили фактические ЛАЧХ и ФЧХ.

Провели аппроксимацию полученных характеристик. После аппроксимации мы можем судить о том какое звено имеет заданное дифференциальное уравнение, а следовательно можем проводить анализ системы, посмотреть какой будет переходный процесс, т. е. как будет себя вести система.

Цель работы достигнута, т. к. мы смогли с помощью аппроксимации получить конкретную передаточную функцию предложенного процесса.

Список используемых источников

1. Власов В.В. Синтез интегральной передаточной функции для объектов управления с распределенными параметрами // Школа академика Власова: Сб. метод. тр. – М.: Буркин, 1998. – 128с.

2. Фролова М.А., Власов В.В. Расчет интегральной передаточной функции. Методические указания к лабораторной работе по курсу “Моделирование систем управления”. – Саратов: СГТУ, 2001. – 12 с.