27

План

Вступ…………………………………………………………………………..3

1. Трикутник, його елементи……………………………………………………5

   1. Медіани трикутника. Центроїд……………………………………..5

   2. Висоти трикутника. Ортоцентр…………………………………….8

   3. Бісектриси трикутника. Інцентр…………………………………..10

2. Бісектральні трикутники…………………………………………………….13

3. Ортоцентричні трикутники…………………………………………………15

4. Особливі точки трикутника ………………………………………………...19

   1. Точки Ейлера……………………………………………….............19

   2. Точки Брокара………………………………………………………20

   3. Точка Лемуана……………………………………………………...22

Структура зв’язків основних елементів точок трикутника………………..24

Висновки……………………………………………………………………...25

Список використаних джерел……………………………………………….26

ВСТУП

Актуальність дослідження. Властивості трикутника були предметом вивчення ще стародавніх греків. У четвертій книзі «Начал» Евклід розв’язує задачу: «Вписати круг у даний трикутник». З розв’язку випливає, що три бісектриси внутрішніх кутів трикутника перетинаються в одній точці – центрі вписаного кола. З розв’язку іншої задачі Евкліда випливає, що перпендикуляри, проведені до сторін трикутника в їх серединах, теж перетинаються в одній точці – центрі описаного кола. В «Началах» не йдеться про те, що і три висоти трикутника перетинаються в одній точці, яка називається ортоцентром (грецьке слово «ортос» означає «прямий», «правильний»). Ця властивість була відома Архімеду, Паппу, Проклу. Архімед довів, що точка перетину медіан є центром тяжіння (барицентром) трикутника.

На вищеназвані чотири точки була звернута особлива увага, і, починаючи з XVIII століття, вони були названі «чудовими» або «особливими» точками трикутника. Дослідження властивостей трикутника, пов'язаних з цими і іншими точками, послужило початком для створення нової гілки елементарної математики – «геометрії трикутника» або «нової геометрії трикутника», одним з родоначальників якої став Леонард Ейлер.

В 1765 році Ейлер довів, що в будь-якому трикутнику ортоцентр, барицентр і центр описаного кола лежать на одній прямій, названій пізніше «прямою Ейлера».

В двадцятих роках XIX століття французькі математики Ж. Понселе, Ш. Бріаншон та інші встановили незалежно один від одного наступну теорему: основи медіан, основи висот і середини відрізків висот, які сполучають ортоцентр з вершинами трикутника, лежать на одному і тому ж колі. Це коло називається «колом дев'яти точок», або «колом Фейєрбаха», або «колом Ейлера». К. Фейербах встановив, що центр цього кола лежить на прямій Ейлера.

Великий внесок в розвиток геометрії трикутника внесли математики XIX – XX століть Лемуан, Брокар, Тебо і інші. Проте не всі «таємниці» трикутника розкрито. Трикутник як геометрична фігура продовжує цікавити математиків. Розглядаються окремі види трикутників, досліджуються їх властивості і т.д.

Об’єктом дослідження є трикутник як геометрична фігура та його властивості.

Предметом дослідження є окремі елементи трикутника, його особливі точки, деякі види трикутників.

Метою дослідження є виділення особливих точок трикутника, дослідження їх властивостей та встановлення особливостей окремих видів трикутників.

Завдання дослідження:

1. Виділення окремих елементів трикутника (медіани, бісектриси, висоти) та дослідження їх властивостей.

2. Розгляд властивостей точок перетину медіан, бісектрис, висот (центроїд, інцентр, ортоцентр).

3. Виокремлення та дослідження деяких видів трикутників (бісектральних, ортоцентричних).

4. Виділення особливих точок трикутника (Ейлера, Брокара, Лемуана), встановлення їх властивостей.

Теоретичне значення роботи полягає у систематизації матеріалу з обраної теми, його узагальненню та ілюстрації основних теоретичних положень у процесі розв’язування геометричних задач.

Практичне значення дослідження полягає в тому, що матеріал, зібраний в роботі, може бути використаний при поглибленому вивченні матеріалу на уроках геометрії, під час розробки та проведення факультативних занять з математики, у процесі підготовки учнів до математичних олімпіад, при вивченні матеріалу відповідної тематики у вищих навчальних закладах.

1. Трикутник, його елементи

Трикутником називається фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки. Точки називаються вершинами трикутника, а відрізки – його сторонами.

Кутом трикутника АВС при вершині А називається кут, утворений півпрямими АВ і АС, так само означаються кути трикутника при вершинах В і С.

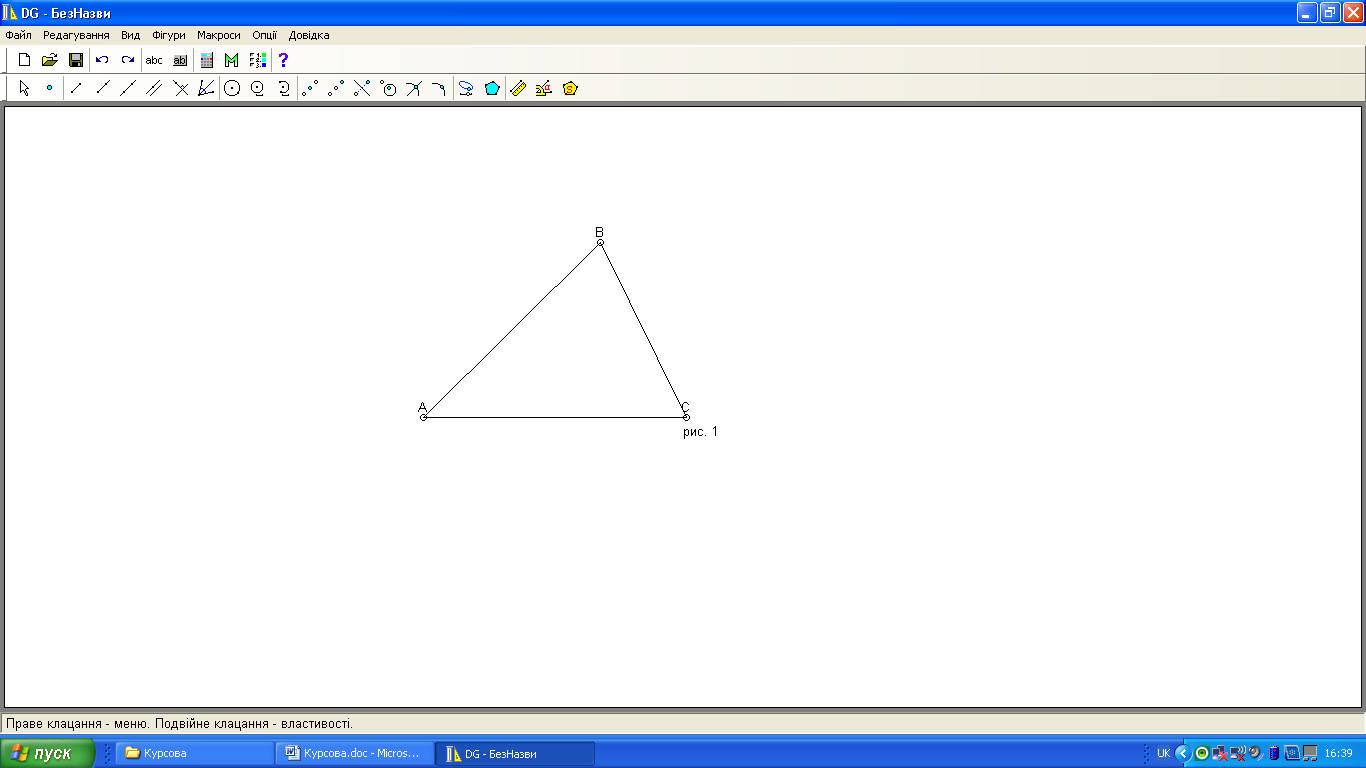
Рис. 1

На рисунку 1 зображений трикутник з вершинами А, В, С; сторонами АВ, ВС, АС та кутами А, В і С.

Нерівність трикутника: Сума довжин будь-яких двох сторін трикутника більша за довжину третьої сторони.

1.1. Медіани трикутника. Центроїд

Медіаною трикутника називається відрізок, що з’єднує вершину трикутника із серединою протилежної сторони.

В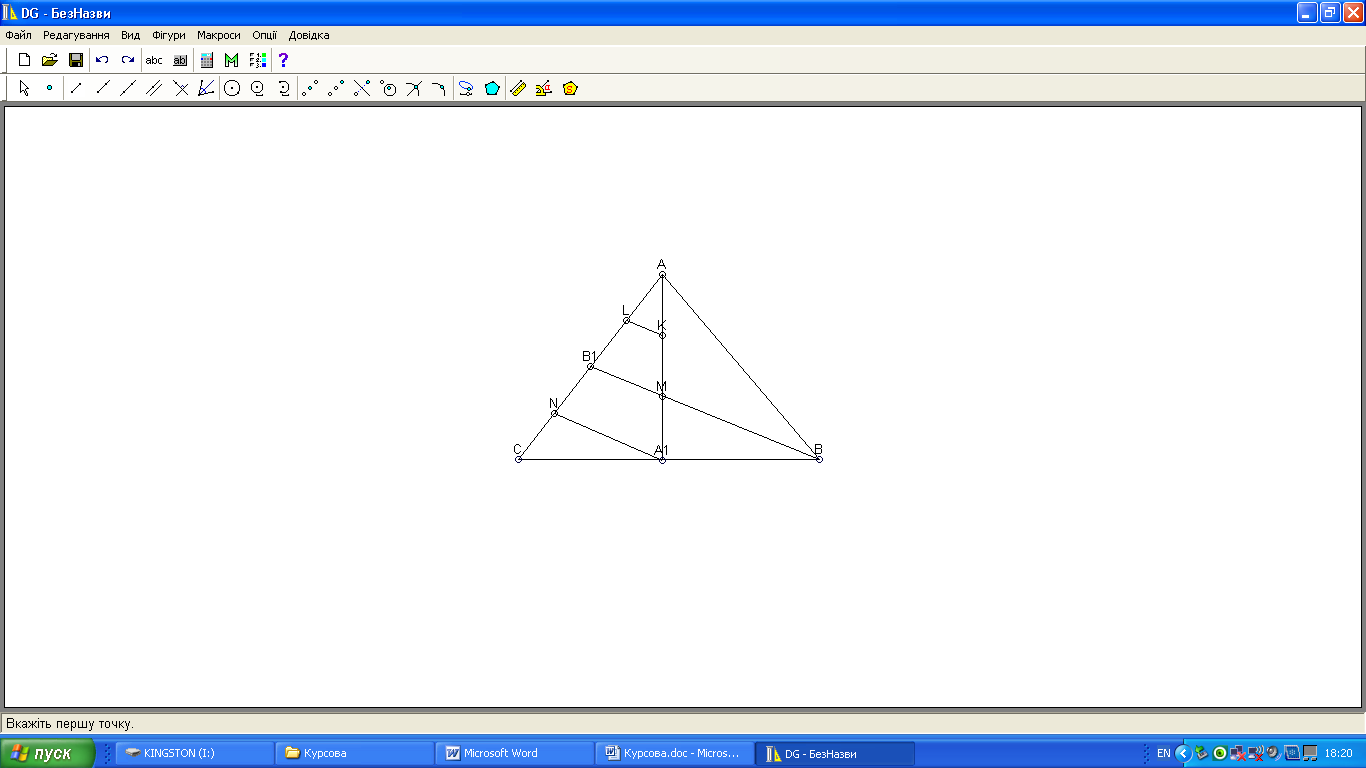ластивість медіани. Три медіани трикутника перетинаються в одній точці і поділяються нею у відношенні 2 : 1, починаючи від вершини трикутника.

Доведення

Нехай К – середина відрізка АМ, В₁ – точка перетину прямої ВМ зі стороною АС (рис. 2). Доведемо, що АВ₁=В₁С, тобто ВВ₁ – Рис. 2

медіана, що проходить через точку М, яка ділить медіану АА₁ у відношенні АМ:МА₁=2:1.

Проведемо через точки К і А₁ паралельно прямій ВВ₁ відрізки KL і А₁N. Оскільки АК=КМ=МА₁ і СА₁=А₁В, то за теоремою Фалеса, одержимо: АL=LВ₁= В₁N=NС.

Отже, АВ₁=В₁С, тобто, ВВ₁ – медіана, проведена із вершини ∆АВС до сторони АС [11].

Точка перетину медіан трикутника називається центроїдом.

Теорема. У середині трикутника АВС (рис. 3) дану деяку точку М – таку, що площі трикутників АМС, ВМС, АМВ рівні між собою. Довести, що М – центроїд трикутника.

Доведення

Н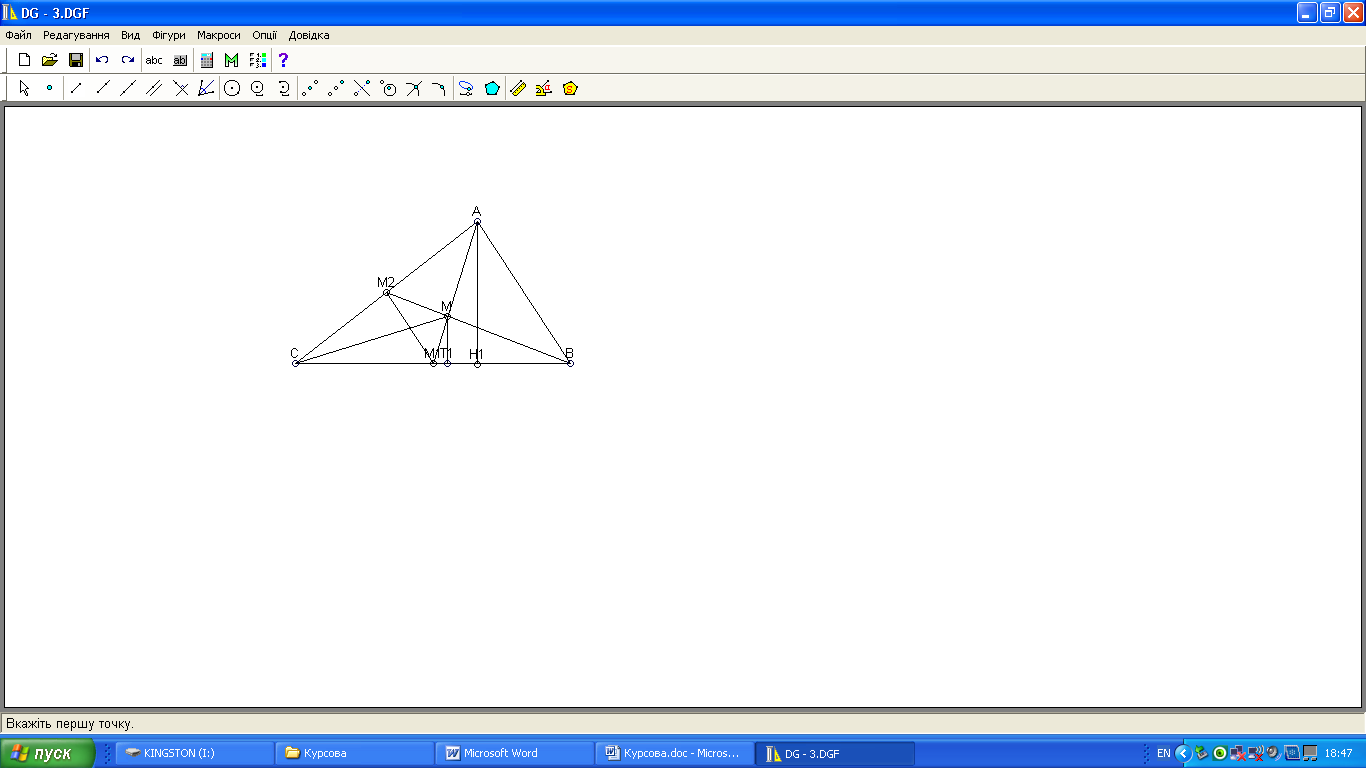ехай площа трикутника АВС дорівнює S. Тоді площі рівновеликих трикутників АВМ, ВМС, АМС дорівнюють кожна. Розглянемо трикутники АВС і ВМС. АН₁ і МТ₁ – висоти цих трикутників. Рис. 3

Тоді =і =, звідки =2.

Аналогічно =2, М₁ і М₂ – точки перетину продовжень АМ і ВМ із сторонами ВС і АС. Отже, АМ₁ і ВМ₂ – медіани, тобто М – центроїд.

З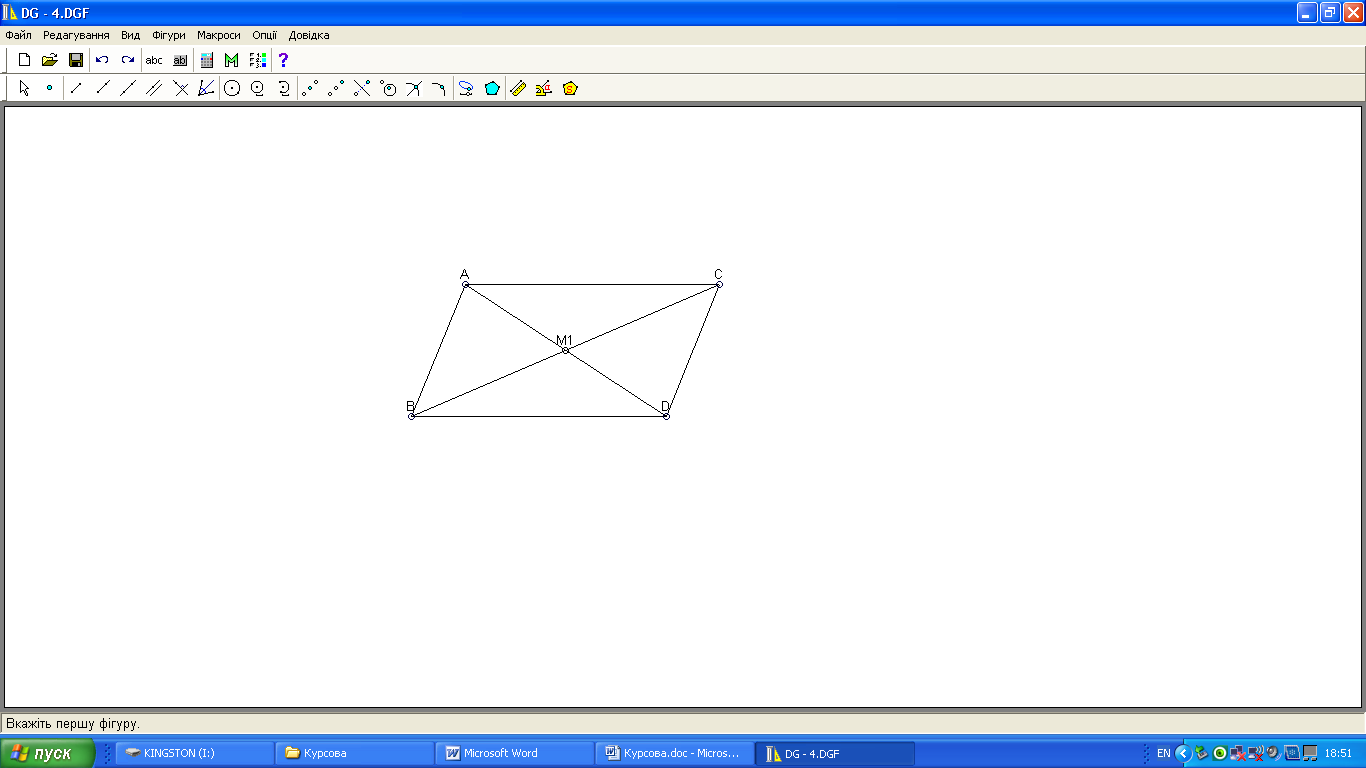адача. У трикутнику АВС m_a²=.

Рис. 4

Доведення

У трикутнику АВС (рис. 4) продовжимо медіану АМ₁ і відкладемо на ній відрізок М₁D=АМ₁. Тоді чотирикутник АВСD – паралелограм, а отже, 2(АВ²+АС²)=АD²+ВС²,

тобто 4m_a²+а²=2(b²+c²).

Звідси дістанемо формулу m_a²=.

Задача (теорема Лейбніца). Довести, що алгебраїчні суми квадратів відстаней від будь-якої точки Х площини від вершини трикутника АВС і від його центроїда М пов’язані співвідношенням:

ХА²+ХВ²+ХС²=АМ²+ВМ²+СМ²+3ХМ².

Доведення

Позначимо через Y проекцію точки Х на медіану (рис. 5). Нехай для визначеності ХМА≤90⁰.

З трикутників ХАМ і ХММ₁:

ХА²=ХМ²+АМ²-,

ХМ₁²= ХМ²+ММ₁²+.

Помножимо другу рівність на 2 і додамо до першої, враховуючи, що 2ММ₁=АМ. Дістанемо:

ХА²+2ХМ₁²=3ХМ²+АМ²+2ММ₁². Рис. 5

Але ХМ₁ – медіана трикутника ВХС, а ММ₁ – медіана трикутника ВМС. За формулою m_a²=.

ХМ₁²=,

ММ₁²=.

Отже, ХА²+ХВ²+ХС²-ВС²=3ХМ²+МА²+МВ²+МС²-ВС².

Тобто ХА²+ХВ²+ХС²=АМ²+ВМ²+СМ²+3ХМ² [5].