Интегралы, зависящие от параметра

§1. Собственные интегралы, зависящие от параметра

1. Определение интегралов, зависящих от параметра

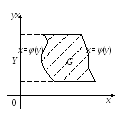Пусть , (y) и (y)- функции, определенные на Y, (y)(y), yY, и функция f(x;y) определена на множестве . Пусть при каждом конкретном значении y=y₀Y функция f(x;y)= f(x;y₀) будет интегрируема на отрезке , то есть y₀Y 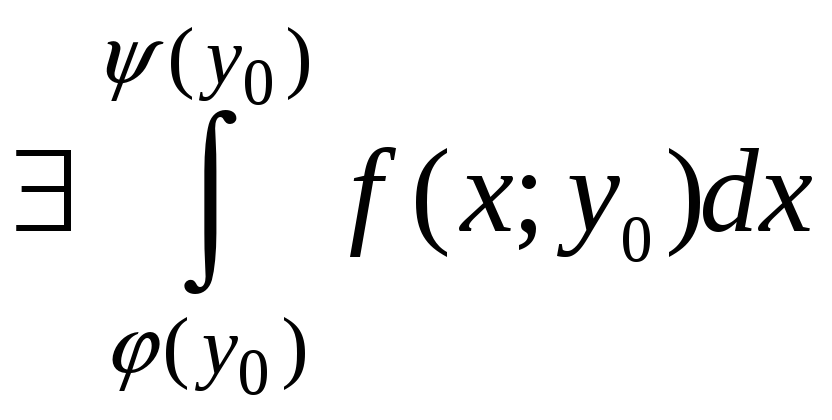. Тем самым определена функция

, yY, (1)

которая называется интегралом, зависящим от параметра, переменная у называется параметром.

Будем рассматривать случай, когда Y=[с;d], функции (y) и (y) непрерывны на [c;d] и (y)(y), y[c;d]. Соответствующую область обозначим G.

Частный случай интеграла типа (1): функции  и  постоянны, то есть интегралы вида:

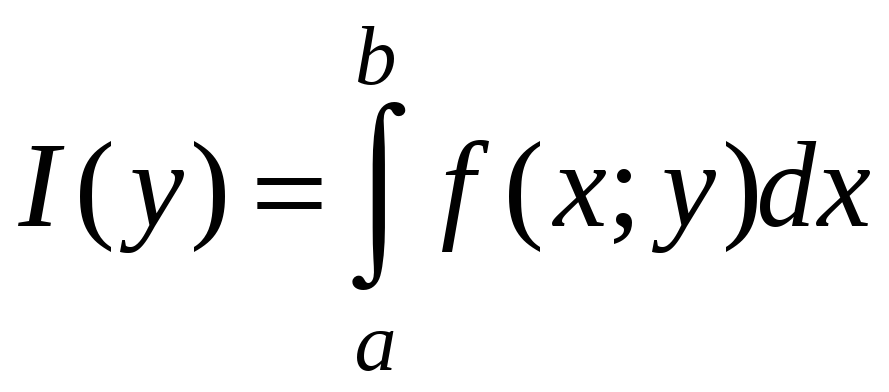. (2)

Задача: изучить свойства функции I(y) (непрерывность, правила дифференцирования и интегрирования) в зависимости от свойств функций f(x;y), (y) и (y).

Пусть , и - функции, определенные на Х, , хХ, и функция f(x;y) определена на множестве . Пусть при каждом конкретном значении хХ функция f(x;y) будет интегрируема на отрезке , то есть 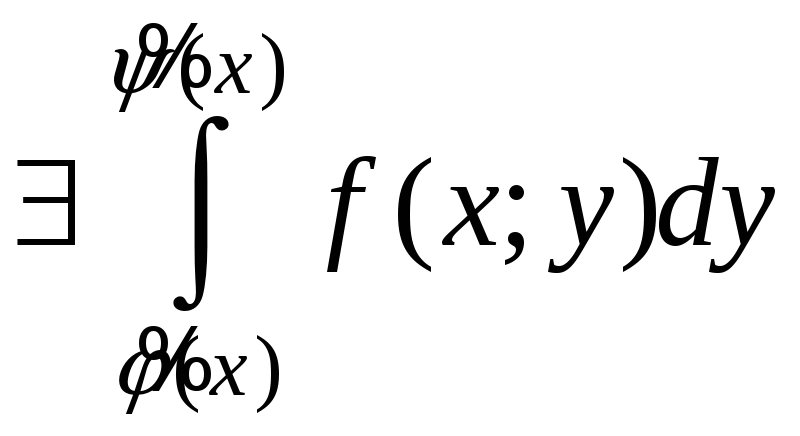. Ясно, что каждому хХ будет отвечать свое определенное значение этого интеграла. Значит, на Х определена функция переменной (параметра) х:

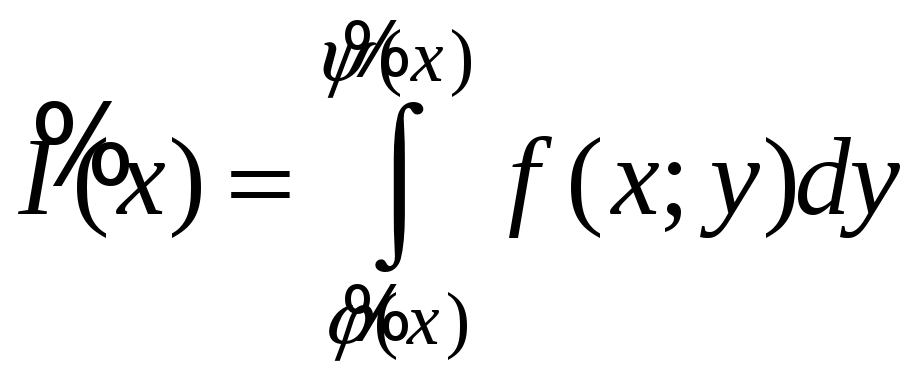. (1)

Частный случай интеграла типа (1): функции и постоянны, то есть интегралы вида: , х[a;b].

2. Равномерная сходимость по параметру семейства функций

Определение 1. Пусть , y₀-предельная точка множества Y. Пусть далее, функция (х) определена для всех хХ, а функция f(x;y), для всех хХ и yY (на ). Если:

1. для функции f(x;y) при yy₀ существует конечная предельная функция

;

2. >0 >0, такое, что при | y-y₀|< будет | f(x;y)-(x)|< сразу для всех хХ, то функция f(x;y) называется равномерно стремящейся на множестве X к функции (х) при yy₀.

Обозначается , yy₀.

Заметим, что

1. в определении 1  не зависит от x;

2. из п.2 следует п.1.

Определение 2. Функция f(x;y) называется равномерно стремящейся на множестве X к функции (х) при yy₀, если .

Теорема 1. Определения 1 и 2 равносильны.

Доказательство.

1. Необходимость: определение 1 определение 2.

Имеем: >0 >0: y: | y-y₀|<, xX выполнено | f(x;y)-(x)|<. Тогда по определению верхней грани .

Получили: >0 >0: y: | y-y₀|< выполнено .

Согласно определению предела функции по Коши это означает, что .

2. Достаточность: определение 2 определение 1.

Имеем: >0 >0: y: | y-y₀|< выполнено .

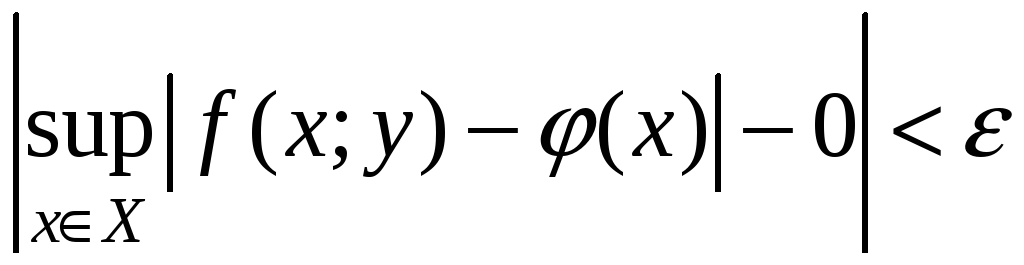Т. к. , то и для всех хХ тем более , т.е. >0 >0: y: | y-y₀|<, xX выполнено | f(x;y)-(x)|<.

Теорема 2 (критерий Коши). Для того чтобы функция f(x;y) при yy₀ равномерно стремилась на множестве Х к некоторой функции необходимо и достаточно, чтобы было выполнено . (3)

Доказательство.

1. Необходимость. Обозначим предельную функцию (х). По условию

выполнено ,

выполнено .

Обозначим . Тогда

:

.

2. Достаточность.

Имеем: выполнено .

В том числе при конкретном значении xX: выполнено .

Тогда по критерию Коши существования предела функции в точке (предел функции в точке а существует >0 =()>0: , выполнено ) получим:

.

Остается показать, что стремление функции f(x;y) к предельной функции (х) при yy₀ происходит равномерно. Переходя в (3) к пределу при yy₀, получим выполнено . По определению 1 функция f(x;y) при yy₀ равномерно стремится на множестве Х к функции (х).

Замечание. Если , , то определение равномерной сходимости по параметру превращается в определение равномерной сходимости последовательности функций на множестве Х:

выполнено .

Пусть далее X=[a;b]. По известной теореме, если последовательность непрерывных функций равномерно сходится к предельной функции на Х, то и эта предельная функция будет непрерывной на Х. Перенесем это утверждение на общий случай.

Теорема 3. Если функция f(x;y) при  yY непрерывна по х в промежутке X=[a;b] и при yy₀ равномерно стремится к предельной функции (х), то функция (х) будет непрерывна на Х.

Доказательство.

Возьмем . Покажем, что соответствующая последовательность значений функции .

По условию при yy₀. По определению 1

>0 >0: y: | y-y₀|<, xX выполнено | f(x;y)-(x)|<.

Т.к. y_ny₀, то по определению: .

В том числе для .

Итак, выполнено .

По определению последовательность равномерно сходится к функции (х) на множестве Х. Тогда по теореме о непрерывности предельной функции равномерно сходящейся последовательности непрерывных функций функция (х) непрерывна на множестве Х.