
- •1 Условие монотонности функции на числовом промежутке
- •2 Необходимое и достаточное условие экстремума функции в точке
- •Достаточное условие существования экстремума
- •3 Наибольшее и наименьшее значение функции на отрезке
- •4 Выпуклые функции. Точки перегиба
- •5 Асимптоты функций
- •6 Полная схема общего исследования функции и построение ее графика
- •Результаты исследования оформим в виде таблицы
Применение дифференциального исчисления к исследованию функций
1 Условие монотонности функции на числовом промежутке
Теорема 1 Необходимое и достаточное условие невозрастания (неубывания) функции на числовом промежутке
Пусть
функция f(х)
непрерывна на числовом промежутке Х,
тогда, для
того, чтобы функция
f(х)
была невозрастающей (неубувающей) на
промежутке Х,
необходимо
и достаточно, чтобы
![]() (
(![]() )
)
для всех внутренних точек этого промежутка.
Замечание
Аналогично можно доказать
условие постоянства функции на числовом
промежутке
Х,
которое заключается в равенстве нулю
ее производной для хХ,
т.е.
![]() .
.
Теорема 2 Достаточное условие возрастания (убывания) функции. Если функция f(х) непрерывна на числовом промежутке Х и имеет положительную (отрицательную) производную во всех внутренних точках этого промежутка, за исключением конечного числа точек, в которых конечная производная не существует или конечная производная равна нулю, то функция f(х) возрастает (убывает) на промежутке Х.
Доказательство этого утверждения состоит из двух этапов:
1)
устанавливается возрастание функции
f(х)
на каждом из промежутков, на которые
делится промежуток Х
указанными в теореме точками (где
![]() не существует, либо равна нулю);
не существует, либо равна нулю);
2) в силу непрерывности функции f(х) на промежутке Х устанавливается ее возрастание (убывание) на всем промежутке Х.
-
Пример
0
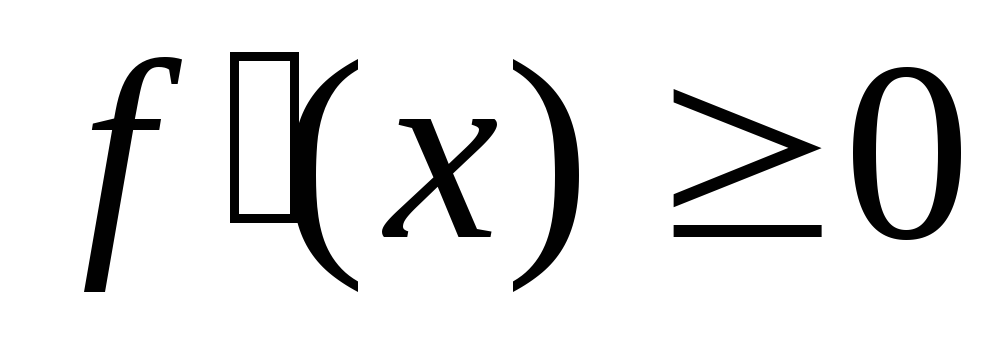
(не убывает)
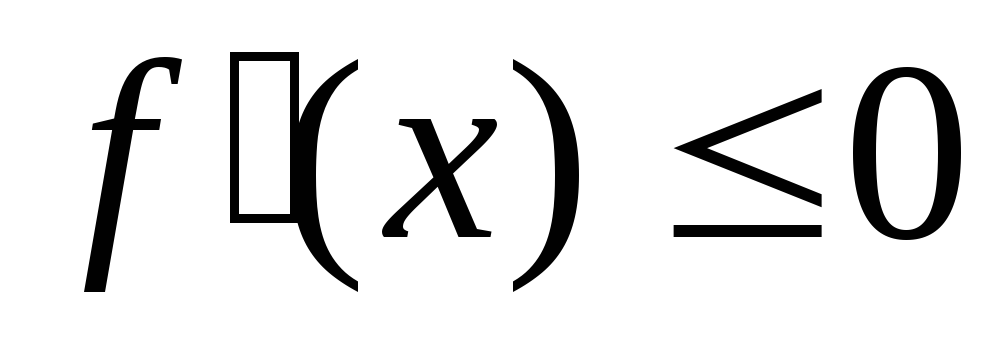
(не возрастает)
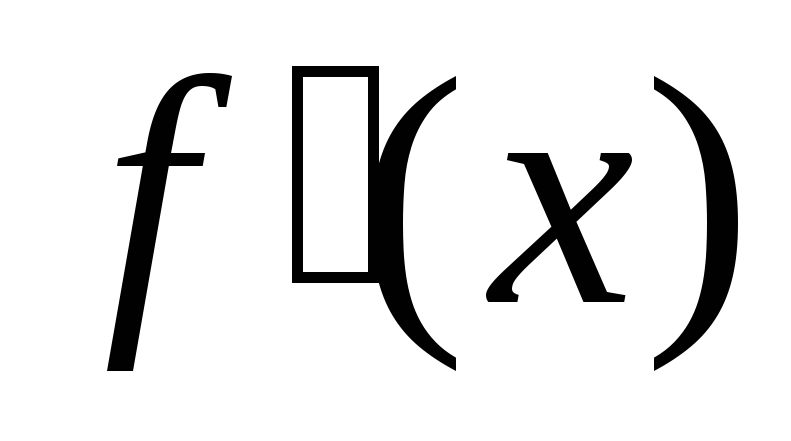
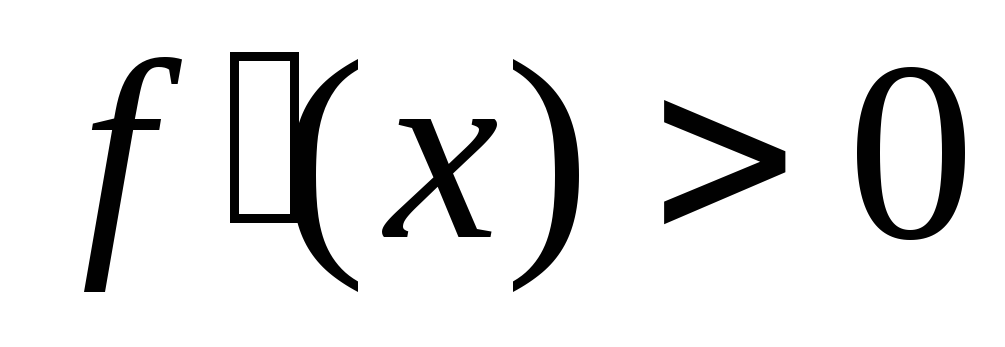

(возрастает)
существует при хХ
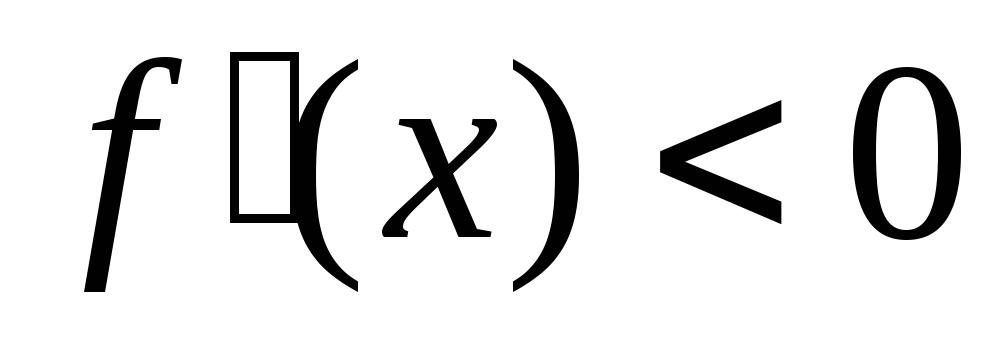

(убывает)
 и
и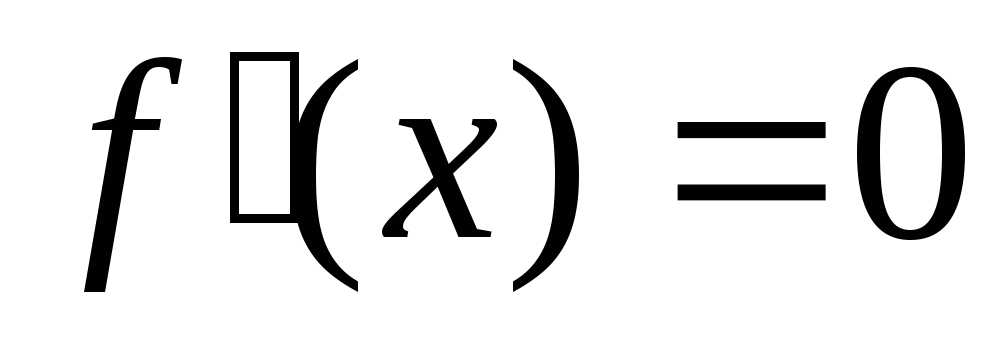 -
у конечного числа точек
-
у конечного числа точек
(возрастает)
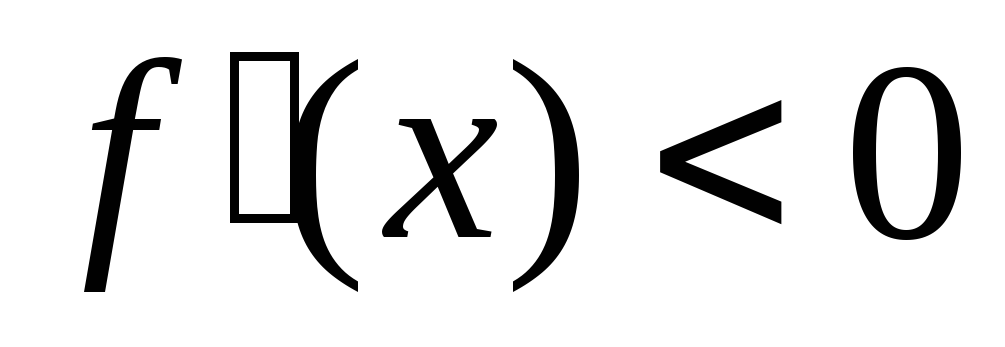
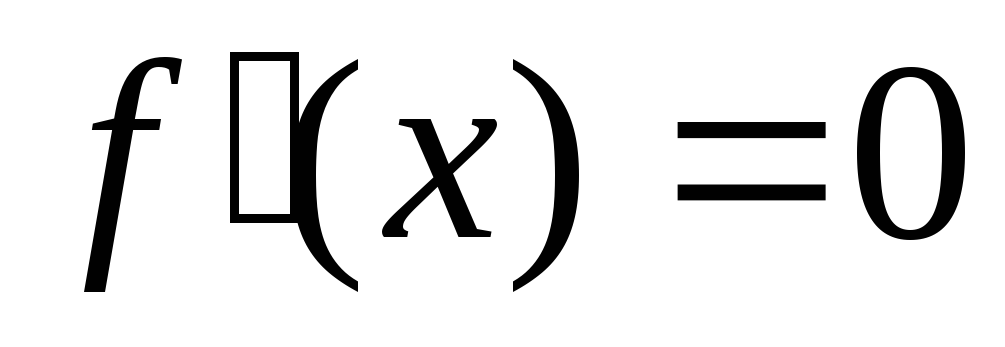 -
у конечного числа точек
-
у конечного числа точек
(убывает)
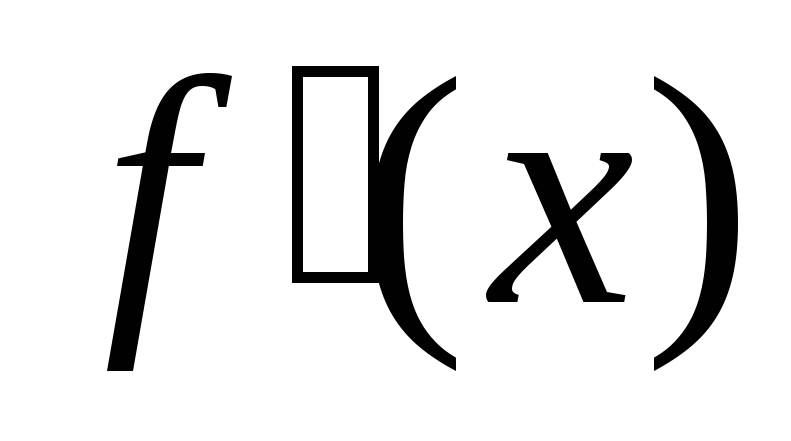
Не существует
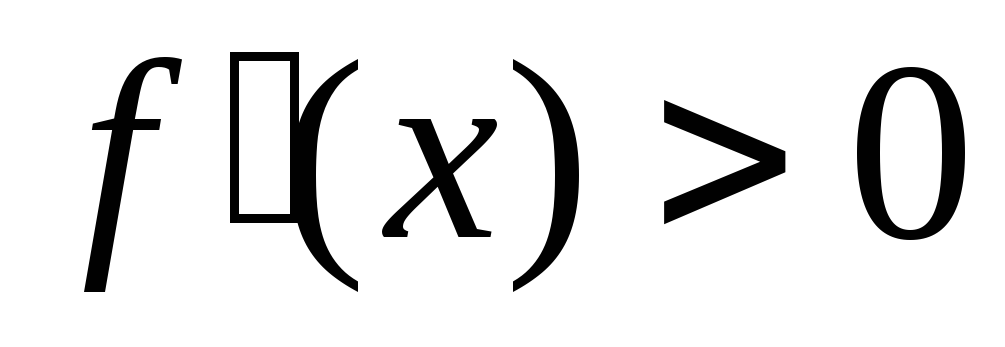

 (возрастает)
(возрастает)у конечного числа точек
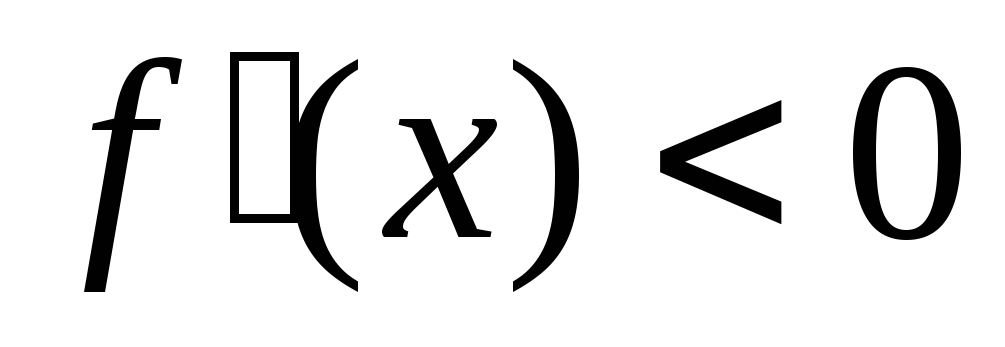
(убывает)
